
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Моделювання ризику при різних рівнях заданого розподілу ймовірностейСодержание книги
Поиск на нашем сайте
Основні питання: 1. Критерії прийняття рішень при заданому розподілі ймовірностей. 2. Критерії прийняття рішень за умов відсутності розподілу ймовірностей. 3. Суперпозиція критеріїв прийняття рішень, обтяжених ризиком.
Мета теми: опрацювання теорії математичних моделей та методів прийняття раціональних рішень за умов заданого розподілу ймовірностей. Основні терміни і поняття теми: критерій Байєса, критерій Бернуллі-Лапласа, математичне сподівання, антагоністичні інтереси середовища. Зміст теми. Згідно з критерієм Байєса (критерій ризику) оптимальним розв’язком
де Етапи розрахунку критерію: 1) розраховується матриця ризиків; 2) розраховуються величини 3) з отриманих значень обирають мінімальне. Отже, оптимальним є варіант, який забезпечує підприємству мінімальний допустимий ризик. Існує інший варіант застосування критерію Байєса, який задовольняє умові:
Тобто, знаходиться математичне сподівання для кожного рішення на основі вихідної матриці прибутків і обирається серед них максимальне. Згідно з критерієм Бернуллі-Лапласа апріорні ймовірності Ці оцінки розподілу апріорних ймовірностей дають змогу застосувати критерії інформаційної ситуації
n – кількість станів економічного середовища. Етапи розрахунку даного критерію: 1) розраховується матриця кількісної оцінки ризику; 2) визначається середнє математичне очікування ризиків; 3) із отриманих даних обирається мінімальне. Іншим способом визначення оптимального варіанту за даним критерієм є вибір рішення яке задовольняє умові:
де Тобто, за основу розрахунків береться вихідна матриця прибутків. В ситуації, коли мається апріорний розподіл ймовірностей настання певного стану Етапи розрахунку критерію: 1) визначається мінімальне значення функціоналу оцінювання для кожного рядку вихідної матриці; 2) для кожного рішення 3) для кожного рішення 4) із отриманих значень Критерій Гурвіца має назву песиміста-оптиміста. При За іншими методиками (за відсутності ймовірностей розподілу станів середовища) на основі матриці прибутків критерій Гурвіца визначається згідно умови:
а на основі ризиків:
Якщо в умові задачі є ймовірність (Р) появи стану середовища (Q), то критерій Гурвіца слід розраховувати з використанням (на основі) критерію Байєса. Якщо ймовірності не вказані, слід скористатися формулами (42) та (43). Література: 1, с. 166-188; 3, с. 205-256; 5, с. 256-300; 10, с. 106-119 Тема 9. Формування інвестиційної стратегії підприємства з урахуванням ризику Основні питання: 1. Сутність та сфери застосування теорії портфелю. 2. Формування портфелю з двох різних акцій. 3. Портфель з багатьох акцій. 4. Оптимізація структури портфелю. 5. Спрощена класична модель формування портфелю.
Мета теми: побудова оптимальних портфелів цінних паперів. Основні терміни і поняття теми: портфель цінних паперів, диверсифікація вкладень, множина допустимих портфелів, множина ефективних портфелів, оптимальний портфель, структура портфеля цінних паперів. Зміст теми. Під теорією портфеля розуміють розподіл коштів між цілим рядом різних активів (акцій, облігацій) в найбільш вигідній та безпечній пропорції. Для портфеля з 2-х акцій характерні такі елементи: · акції А і Б з відповідними номерами 1 та 2; · норми прибутку · варіації · середнє квадратичне відхилення Сподівана норма прибутку портфеля з 2-х акцій
де Ризик такого портфеля можна обчислити за допомогою варіації
де Середнє квадратичне відхилення портфеля з 2-х акцій
Частки 2-х різних акцій в даному портфелі
а, відповідно, Величина кожної з часток акцій залежить від ступеню кореляції між цими акціями ( Випадок, коли
або Ризик портфеля, виражений як середньоквадратичне відхилення в цьому випадку дорівнюватиме:
Аналіз рівняння (49) показує, що ризик портфеля в цьому випадку можна суттєво зменшити. Якщо
Тобто, у випадку абсолютної від’ємної кореляції є можливість обрати таку структуру портфеля, який цілком буде позбавлений ризику. Випадок, коли
Середньоквадратичне відхилення розраховується за формулою:
Звідси витікає, що є можливість часткової редукції ризику портфелю 2-х акцій. Частки акцій розраховуються за формулою:
Перейдемо тепер до загального випадку, коли до складу портфеля залучено багато різних акцій. Вихідна інформація для визначення структури портфеля з багатьох акцій наступна: n – кількість різних акцій, що залучаються до портфеля, пронумерованих від 1 до n; Очевидно, що Середня сподівана норма прибутку для портфеля з багатьох акцій розраховується за формулою:
Величина варіації:
Середньоквадратичне відхилення:
З формули (57) витікає, що варіацію, тобто ризик портфеля, можна трактувати як суму двох складових. Перша складова віддзеркалює індивідуальний ризик кожної з акцій, друга складова характеризується взаємозв’язками між парами акцій, тобто показує вплив коефіцієнтів кореляції пар акцій на ризик портфеля: від’ємні величини коефіцієнтів кореляції призводять до зменшення варіації портфеля. Література: 1, с. 124-164; 9, с. 65-116
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.008 с.) |

 слід вважати такий, для якого математичне сподівання функціоналу оцінювання досягає свого найменшого значення:
слід вважати такий, для якого математичне сподівання функціоналу оцінювання досягає свого найменшого значення: , (36)
, (36)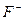
 , які називають Байєсовським ризиком для розв’язку
, які називають Байєсовським ризиком для розв’язку  .
. (37)
(37) станів середовища рівні, тобто згідно з «принципом недостатніх підстав»:
станів середовища рівні, тобто згідно з «принципом недостатніх підстав»:  .
. . Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні критерію Байєса та принципу недостатніх підстав для знаходження оцінок апріорних ймовірностей
. Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні критерію Байєса та принципу недостатніх підстав для знаходження оцінок апріорних ймовірностей  , (38) де
, (38) де  , (39)
, (39)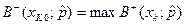 , (40)
, (40) (41)
(41) і водночас йдеться про антагоністичні інтереси середовища
і водночас йдеться про антагоністичні інтереси середовища  , що мають для керівництва фірми пріоритет, то має місце інформаційна ситуація
, що мають для керівництва фірми пріоритет, то має місце інформаційна ситуація  , при якій за критерій прийняття рішення обирається критерій Гурвіца.
, при якій за критерій прийняття рішення обирається критерій Гурвіца.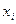 визначається
визначається  ;
; ;
;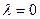 критерій Гурвіца співпадає з максимальним критерієм, а при
критерій Гурвіца співпадає з максимальним критерієм, а при  - з критерієм Вальда.
- з критерієм Вальда.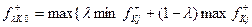 , (42)
, (42)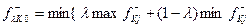 (43)
(43) та
та  ;
;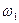 та
та 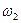 ;
; та
та 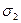 .
. розраховується за формулою:
розраховується за формулою: , (44)
, (44) та
та 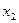 - частки кожної акції в портфелі
- частки кожної акції в портфелі  .
. :
: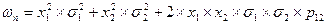 , (45)
, (45) - кореляція двох різних видів акцій.
- кореляція двох різних видів акцій. розраховується за формулою:
розраховується за формулою: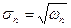 (46)
(46) розраховуються за формулою:
розраховуються за формулою: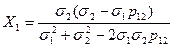 , (47)
, (47) .
. , (48)
, (48)

 (49)
(49)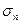 прирівняти до нуля, то
прирівняти до нуля, то (50)
(50) (51)
(51) (52)
(52) , (53)
, (53) (54)
(54) - сподівана норма прибутку і-ої акції (і=
- сподівана норма прибутку і-ої акції (і=  ),
),  - коефіцієнт кореляції і-ої та j-ої акції (
- коефіцієнт кореляції і-ої та j-ої акції ( );
);  - частка і-ої акції, залученої до портфеля (і=
- частка і-ої акції, залученої до портфеля (і=  (55)
(55)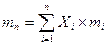 (56)
(56) (57)
(57)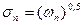 (58)
(58)


