
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Основні засади моделювання ризику на основі теорії ігорСодержание книги
Поиск на нашем сайте Основні питання: 1. Сутність та сфери застосування теорії гри. 2. Понятійний апарат теорії ігор. 3. Критерії прийняття рішень у ситуації, що характеризується невизначеністю. Мета теми: опрацювання теорії математичних моделей та методів прийняття раціональних рішень за умов невизначеності. Основні терміни і поняття теми: математичні моделі, теорія ігор, функціонал оцінювання, інформаційна ситуація, критерій Вальда, критерій Севіджа. Зміст теми. Під теорією ігор розуміють теорію математичних моделей та методів прийняття раціональних рішень за умов конфлікту та невизначеності. Ситуація прийняття рішень характеризується множиною {X;Q;F}, де
У розгорнутій формі ситуація прийняття рішення характеризується матрицею, елементами якої є:
Процес прийняття рішень за умов ризику складається з таких етапів: 1) формування множини рішень Х та множини станів економічного середовища Q; 2) визначення та формалізація основних показників ефективності та корисності, що входять у функціонал оцінювання 3) визначення інформаційної ситуації, що характеризує стратегію поводження економічного середовища; 4) вибір критерію прийняття рішень відповідно до інформаційної ситуації; 5) прийняття оптимального рішення за обраним критерієм. Під інформаційною ситуацією (І) розуміють певний ступінь градації невизначеності вибору середовища своїх станів у момент прийняття рішення:
Для першої інформаційної ситуації найбільш важливим є критерій Байєса, для четвертої – Лапласа, для п’ятої – Вальда, Севіджа, для шостої – Гурвіца. Критерій Вальда ґрунтується на максимінному принципі для функціоналу F, що полягає в прийнятті такого рішення
Знак «+» поряд із Етапи розрахунку даного критерію: 1) визначається найменший елемент в кожному рядку матриці; 2) серед цих найменших елементів знаходиться максимальне значення. Стратегія, обрана за критерієм Вальда (стратегія песиміста) дає гарантований виграш при найгіршому стані середовища. Згідно із критерієм Севіджа (мінімаксний критерій) оптимальним розв’язком
Знак «-» означає, що за цим критерієм оптимізується ризик. Етапи розрахунку даного критерію: 1) у кожному стовпчику вихідної матриці знаходиться максимальне значення; 2) отримані максимальні значення віднімають від кожного елементу відповідного стовпчика (при цьому враховують додатні та від’ємні знаки) і заносять їх до матриці ризиків (по модулю); 3) у кожному рядку матриці ризиків знаходиться максимальне значення; 4) із отриманих максимальних значень знаходиться мінімальне значення. Критерій Севіджа є менш консервативним порівняно з критерієм Вальда і ґрунтується на принципі оптимізації ризику. Література: 1, с. 166-188; 3, с. 205-256; 5, с. 256-300; 10, с. 106-119; 13, с. 187-219
|
|||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

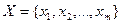 - множина рішень щодо об’єкта керування (альтернативні варіанти обсягів виробництва продукції),
- множина рішень щодо об’єкта керування (альтернативні варіанти обсягів виробництва продукції),  - множина станів економічного середовища (попит на продукцію),
- множина станів економічного середовища (попит на продукцію),  - функціонал оцінювання, в якості якого можуть виступати такі показники, як прибуток (збитки), витрати тощо.
- функціонал оцінювання, в якості якого можуть виступати такі показники, як прибуток (збитки), витрати тощо.
 - кількісні оцінки прийнятого рішення
- кількісні оцінки прийнятого рішення 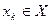 за умови, що середовище знаходиться в стані
за умови, що середовище знаходиться в стані  :
: - перша інформаційна ситуація, яка характеризується заданим розподілом апріорних ймовірностей на елементах множини Q;
- перша інформаційна ситуація, яка характеризується заданим розподілом апріорних ймовірностей на елементах множини Q; - друга інформаційна ситуація, яка характеризується заданим розподілом з невідомими параметрами;
- друга інформаційна ситуація, яка характеризується заданим розподілом з невідомими параметрами; - третя інформаційна ситуація, яка характеризується заданою системою лінійних співвідношень на компонентах апріорного розподілу станів середовища;
- третя інформаційна ситуація, яка характеризується заданою системою лінійних співвідношень на компонентах апріорного розподілу станів середовища; - четверта інформаційна ситуація, яка характеризується невідомим розподілом ймовірностей на елементах множини Q;
- четверта інформаційна ситуація, яка характеризується невідомим розподілом ймовірностей на елементах множини Q; - п’ята інформаційна ситуація, яка характеризується антагоністичними інтересами середовища в процесі прийняття рішення;
- п’ята інформаційна ситуація, яка характеризується антагоністичними інтересами середовища в процесі прийняття рішення; - шоста інформаційна ситуація, яка характеризується як проміжна між
- шоста інформаційна ситуація, яка характеризується як проміжна між  , яке задовольняє умову:
, яке задовольняє умову: (34)
(34) означає, що за даним критерієм оптимізується виграш, ефективність тощо.
означає, що за даним критерієм оптимізується виграш, ефективність тощо. є такий, який задовольняє умову:
є такий, який задовольняє умову: (35)
(35)


