
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерпретація результатів розрахунку Z-показникаСодержание книги
Поиск на нашем сайте
Модель Спрінгейта передбачає розрахунок інтегрального показника, за допомогою якого здійснюється оцінка імовірності визнання підприємства банкрутом, за формулою:
Z = 1,03 * A + 3,07 * B + 0,66 * C + 0,4 * D, (21)
де А – робочий капітал / загальна вартість активів; В – прибуток до сплати податків та відсотків / загальна вартість активів; С – прибуток до сплати податків / короткострокова заборгованість; D – обсяг продажу / загальна вартість активів. Інтервал значень результуючого показника Z поділений на основі єдиної критичної точки, яка відповідає значенню Z-показника 0,862. Таким чином, підприємство з достовірністю 92% може бути віднесене до категорії потенційних банкрутів, якщо розрахункове значення Z-показника для даного підприємства менше за 0,862. Основними обмеженнями всіх зазначених моделей діагностики банкрутства є насамперед неврахування специфіки та реалій економічного життя окремих країн, а також відсутність у моделях факторів, які враховували б вплив галузевої належності підприємства. Таким чином, прогнозування банкрутства на основі згаданих методик можливе лише у формі додаткових індикаторів визначення загального економічного потенціалу підприємства. Література: 8, с. 115-134.
Модуль 2. Моделювання ризику та основні підходи щодо управління ним
Тема 6. Концепція корисності та оптимізація ризику Основні питання: 1. Понятійний апарат теорії корисності. 2. Сутність лотереї за Нейманом - Моргенштерном. 3. Оптимізація рішення в умовах несхильності особи до ризику. 4. Прийняття рішень особою, схильною до ризику. 5. Байдужість до ризику. Криві байдужості. Мета теми: опанування методологією обґрунтування ризикованих рішень на основі порівняння функцій розподілу ефективності. Основні терміни і поняття теми: корисність, пріоритети, лотерея, детермінований еквівалент, криві байдужості, схильність до ризику, несхильність до ризику, нейтральність до ризику, премія за ризик. Зміст теми. Для задач прийняття рішень за умов невизначеностіта ризику принцип оптимальності нерідко будується у вигляді функції корисності. Оскільки при наявності ризику результати рішень залежать від випадкових величин, то для порівняння їх ефективності необхідно вміти порівнювати функції розподілу ефективності. Найбільш загальний підхід щодо оцінки ступеня ризику полягає у введенні функції корисності. Концепція функції корисності є одним із важливих елементів будь-якої сучасної економічної теорії. Вона дозволяє здійснити співвимірність споживчих елементів різних товарів. Застосовуючи різні функції корисності, можна описати будь-які варіанти оцінки випадкової економічної ситуації у вигляді сподіваного значення такої функції.
Корисність визначає ступінь задоволення, яке одержує суб’єкт від споживання товару чи виконання будь-якої дії. Функцією корисності називають неперервну дійсну функцію U(•), визначену на елементах множини х і для якої
Вираз х>y означає, що елемент х «не гірший», ніж елемент у. Функція корисності співвідносить кожному набору споживчих товарів певне число в такий спосіб, що число, яке відповідає набору А, буде більшим, ніж число, що відповідає набору Б, якщо набір А пріоритетніший, ніж набір Б (А>Б) Під лотереєю Неймана-Моргенштерна розуміють ситуацію, в якій особа може отримати х’ з імовірністю р(х’), або х’’ з імовірністю 1-р(х’):
де х’ та х’’ – відповідно мінімальне та максимальне значення аналізуємого споживчого набору, яким приписують доволі числові значення U’=U(x’) та U”=U(x”), але так, щоб U”>U’. Математичне сподівання виграшу
де Xs – величина певних витрат; Ps – ймовірність отримання певних виграшей. Сподівана користь
Тобто, корисність ансамблю результатів збігається з математичним сподіванням корисності результатів. Детермінований еквівалент лотереї L являє собою гарантовану суму
Якщо детермінований еквівалент перевищує середній виграш лотереї, то особа схильна до ризику, у протилежному випадку – не схильна до ризику. Для зростаючих функцій корисності премією за ризик П(х) в лотереї L є різниця між сподіваним виграшем М(х) та детермінованим еквівалентом
П(х)=М(х)- Премія за ризик – це сума, якою суб’єкт керування згоден знехтувати з середнього виграшу за те, щоб уникнути ризику. Несхильною до ризику вважається особа, для якої привабливішою є альтернатива отримання гарантованого середнього виграшу лотереї, ніж участь у лотереї. Схильною до ризику вважається особа, яка бажає взяти участь у лотереї замість того, щоб отримати гарантований середній виграш у лотереї. Якщо особі байдуже, чи брати участь у лотереї, чи отримати гарантований середній виграш, то вона вважається байдужою до ризику. Умова несхильності особи до ризику приймає вид: U(M(x))>M(U(x)), (27) тобто корисність математичного сподівання виграшу повинна бути більшою, ніж математичне сподівання корисності виграшів. Функція корисності особи, несхильної до ризику має вид: U(x)=log(a+b),x>-b, (28)
Рис.1. Функція корисності особи, що несхильна до ризику.
Згідно з рис.1 з кожною додатковою одиницею доходу зменшується його гранична корисність. Умова схильності особи до ризику має вигляд: U(M(x))<M(U(x)) (30) Функція корисності зі схильністю до ризику має вигляд:
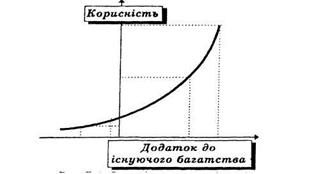
Рис.2. Функція корисності особи, схильної до ризику.
Згідно з рис.2 приріст корисності від виграшу більший, ніж зменшення корисності від програшу. Але статистичні дослідження та емпіричний досвід свідчать, що звичайна людина може мати схильність до ризику, коли йдеться про невеликі суми відносно її статку, та надзвичайно обережна при значних сумах. Умова байдужості особи до ризику має вигляд: U(M(x))=M(U(x)), (32) Функція корисності особи байдужої до ризику має вигляд: U(x)=a+bx; b>0, (33)
Рис.3. Графік кривих байдужості.
Криві байдужості можна трактувати як різні рівні значень функцій корисності. Крива 1 окреслює всі можливі пари значень норм прибутку і ризику, для яких рівень корисності дорівнює 5 одиницям, тобто корисність однакова як для сполучення «велика норма прибутку – більший ступінь ризику», так і для сполучення «менша норма прибутку – менший ступінь ризику». Досить часто зміни значень норми прибутку і ризику призводять до зміни рівня корисності. Так, зростання норми прибутку (m) при незмінному ступені ризику Література: 1, с. 108-122; 3, с. 185-204; 9, с. 26-44; 10, с. 139-149
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.163.233 (0.011 с.) |

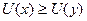 , якщо х>y. (22)
, якщо х>y. (22)
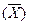 визначається за формулою:
визначається за формулою: , (23)
, (23)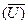 визначається за формулою:
визначається за формулою: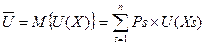 (24)
(24) , отримання якої еквівалентне участі в лотереї, тобто
, отримання якої еквівалентне участі в лотереї, тобто  . Отже,
. Отже, 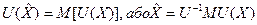 (25)
(25)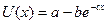 ,b>0,
,b>0,  , (29)
, (29)
 (31)
(31)

 означає перехід на іншу «вищу» криву байдужості, що відповідає більшому значенню функції корисності (на рис. 1.3 перехід з точки А в точку В). Аналогічно, зменшення ступеня ризику при незмінній нормі прибутку також означає перехід на криву байдужості, що відповідає більшому значенню функції корисності (перехід з точки А в точку С на рис.3).
означає перехід на іншу «вищу» криву байдужості, що відповідає більшому значенню функції корисності (на рис. 1.3 перехід з точки А в точку В). Аналогічно, зменшення ступеня ризику при незмінній нормі прибутку також означає перехід на криву байдужості, що відповідає більшому значенню функції корисності (перехід з точки А в точку С на рис.3).


