
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коротко сформулювати предмет вивчення теорії ймовірностейСодержание книги
Поиск на нашем сайте Коротко сформулювати предмет вивчення теорії ймовірностей Предметом теорії ймовірностей є вивчення вірогідних закономірностей масових однорідних випадкових подій.Знання закономірностей, яким підкоряються масові випадкові події, дозволяє передбачати, як ці події будуть протікати. Наприклад, хоча, як було вже сказане, не можна наперед визначити результат одного кидання монети, але можна пророчити, причому з невеликою погрішністю, число появ «герба», якщо монета буде кинуте досить велике число раз. При цьому передбачається, звичайно, що монету кидають у тих самих умовах. Методи теорії ймовірностей широко застосовуються в різних галузях природознавства і техніки: у теорії надійності, теорії масового обслуговування, у теоретичній фізиці, геодезії, астрономії, теорії стрілянини, теорії помилок спостережень, теорії автоматичного керування, загальної теорії зв'язку й у багатьох інших теоретичних і прикладних науках. Теорія ймовірностей служить також для обґрунтування математичної і прикладної статистики, що у свою чергу використовується при плануванні й організації виробництва, при аналізі технологічних процесів, попереджувальному і приймальному контролі якості продукції і для багатьох інших цілей.
Дати означення достовірної, неможливої і випадкової подій Достовірною подією в теорії ймовірностей називається подія, яка в результаті досвіду або спостереження неодмінно має статися. Неможли́вою поді́єю в теорії ймовірності називається подія, яка в результаті досліду статися не може. Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність p (0 ≤ p ≤ 1) того, що вона відбудеться при заданих умовах. Випадкова подія є підмножиною простору елементарних подій. Які події називаються сумісними, несумісними? Дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої. У теорії ймовірностей дві події називаються несумісними, якщо вони не можуть відбутися одночасно.
Що таке повна група подій, протилежні події? Повною групою подій у теорії ймовірності називається система випадкових подій така, що в результаті проведеного випадкового експерименту неодмінно станеться одне з них. Дві події називаються протилежними, якщо одна, і тільки одна, з них обов’язково здійсниться в даному випробуванні.
Дати класичне означення ймовірності, вказати межі його застосування. Ймовірність події А – це відношення наслідків, що сприяють появі події до загального числа можливих наслідків. P(A)= m /n мова рівноможливості, як правило, спостерігається в штучно організованих експериментах, які забезпечують певну симетрію елементарних подій (виходів) так, що немає об’єктивних причин вважати одну з елементарних подій більш ймовірною, в порівнянні з іншими.
6) Дати означення і навести формулу для обчислення кількості розміщень, перестановок, сполучень. Розміщення – це сполуки в яких можна розмістити k елементів з числа n заданих, які відрізняються між собою або самими елементами або їх порядком.
Перестановки – це сполуки, що відрізняються тільки порядком елементів. Рn=n! Сполучення – це сполуки які містять k елементів загального числа n і відрізняються між собою тільки самими елементами.
Дати геометричне означення ймовірності. Ймовірністю називається відношення міри області S2 до міри області S1. P(A)=m(S2)/m(S1)
Що таке відносна частота події? Статистичне означення ймовірності. Відносною частотою події А серії випробувань називається відношення числа випробувань де поява з’явилася до загального числа проведених дослідів. Ймовірністю випадкової події називається стале число біля якого ґрунтуються відносні частоти появи цієї події в міру збільшення числа випробувань.
Які властивості ймовірності ви знаєте? 1. Ймовірність достовірної події =1 2. Ймовірність неможливої події =0 3. Ймовірність випадкової події є невід’ємне число <1
Що таке сума подій? Навести приклади. Сума кількох подій – це подія, яка полягає в появі принаймі однієї події.
Що таке добуток подій? Навести приклад. Добуток подій називається подія, яка полягає принаймі в спільній всіх подій.
Сформолювати і записати теореми обчислення ймовірностей А) суми несумісних подій Ймовірність суми двох несумісних подій дорівнює сумі ймовірності цих подій. С=А+В Р(С)=Р(А)+Р(В) Б) суми сумісних подій (два варіанта) 1. Ймовірність появи принаймі однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи. Р(С)=Р(А)+Р(В)-Р(АВ) 2. Ймовірність появи принаймі однієї з сумісних подій дорівнює різниці між 1 і ймовірністю добутків протилежних подій.
В) Добуток незалежних подій Ймовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій. Р(А*В)=Р(А)*Р(В) Г) добуток залежних подій Ймовірність добутку залежних подій дорівнює добутку ймовірності однієї події з них на умовну ймовірність другої, якщо перша вже відбулася
Що таке умовна ймовірність? Нехай події А і В – залежні та подія А вже відбулася. Число, яке виражає ймовірність події В за умови, що подія А вже відбулася, називається умовною ймовірністю події В відносно події А і позначається:
Що таке надійність? Надійністю називають ймовірність безвідмовної роботи пристрою чи системи протягом певного відрізку часу.
Коротко сформулювати предмет вивчення теорії ймовірностей Предметом теорії ймовірностей є вивчення вірогідних закономірностей масових однорідних випадкових подій.Знання закономірностей, яким підкоряються масові випадкові події, дозволяє передбачати, як ці події будуть протікати. Наприклад, хоча, як було вже сказане, не можна наперед визначити результат одного кидання монети, але можна пророчити, причому з невеликою погрішністю, число появ «герба», якщо монета буде кинуте досить велике число раз. При цьому передбачається, звичайно, що монету кидають у тих самих умовах. Методи теорії ймовірностей широко застосовуються в різних галузях природознавства і техніки: у теорії надійності, теорії масового обслуговування, у теоретичній фізиці, геодезії, астрономії, теорії стрілянини, теорії помилок спостережень, теорії автоматичного керування, загальної теорії зв'язку й у багатьох інших теоретичних і прикладних науках. Теорія ймовірностей служить також для обґрунтування математичної і прикладної статистики, що у свою чергу використовується при плануванні й організації виробництва, при аналізі технологічних процесів, попереджувальному і приймальному контролі якості продукції і для багатьох інших цілей.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |





 або
або 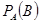 .
.


