
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття. Операції над подіямиСодержание книги
Поиск на нашем сайте
Теорія ймовірностей – це математична наука, що вивчає закономірності випадкових явищ. Випробування — реальний або мислений експеримент (що виконується за певної незмінної сукупності умов), результати якого піддаються спостереженню. Подія — результат випробування.
Випадкові події позначаються літерами A, B, C, D, …. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається літерою U. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається літерою V. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події, які не можна розкласти на простіші, називаються елементарними. Можлива елементарна подія — це кожний із можливих результатів окремого випробування. Сума подій. Подія А називається сумою подій В і С, тобто А = В + С або Добуток подій. Подія А називається добутком подій В і С, тобто
Різниця подій. Подія А називається різницею подій В і С, тобто Сумісними називаються події, коли поява однієї із подій не виключає появу інших. Події В і С у даному випробуванні називаються несумісними, якщо поява однієї з них виключає появу іншої в даному випробуванні:
Події В і С називаються рівноможливими у даному випробуванні, якщо є підстава вважати, що жодна з них не є об’єктивно більш можливою, ніж інша. Події Події
ОЗНАЧЕННЯ ЙМОВІРНОСТІ ПОДІЇ. БЕЗПОСЕРЕДНЄ ОБЧИСЛЕННЯ ІМОВІРНОСТЕЙ Ймовірністю події А називається числова міра об’єктивної можливості настання цієї події в певному випробуванні. Позначається така ймовірність Р (А). Властивості ймовірності 1. Ймовірність достовірної події 2. Ймовірність неможливої події 3. Ймовірність будь-якої випадкової події Класичне означення ймовірності. Ймовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій:
Розв’язання. а) Позначимо А = {вибраний чоловік-адміністратор} У банку працюють 100 чоловік, n = 100. З них 15 — чоловіки-адміністратори, m = 15, отже Р (A)= 15/100 = 0,15. б) B = {вибрана жінка-операціоніст } 35 службовців у банку — жінки-операціоністи, отже P (В) = 35/100 = 0,35. в) С = {вибраний чоловік} 40 службовців банку — чоловіки, отже Р (С)= 40/100 = 0,40. г) D = { вибраний операціоніст} Із загальної кількості службовців банку 60 — операціоністи, отже P (D)= 60/100= 0,60.
Елементи комбінаторики Розміщення. Кінцеві впорядковані підмножини, що містять m елементів, узятих з n елементів основної множини, називаються розміщеннями з n елементів по m елементів. Число всіх можливих розміщень з n елементів по m позначають
Перестановки. Різні кінцеві впорядковані множини, що складаються зі всіх елементів деякої заданої множини називаються перестановками. Якщо основна множина містить n елементів, то число перестановок позначається
Сполучення. Кінцеві невпорядковані підмножини, які містять m різних елементів з n елементів заданої множини називаються сполученнями з n елементів по m. Число сполучень з n елементів по m позначають
Розміщення із повторенням. Беремо з множини навмання m елементів з поверненням. Тоді у фіксованій підмножині кожний елемент може повторитися m разів. Елементарною подією у випробуванні буде розміщення з n елементів по m із повторенням, а кількість таких розміщень
Перестановки із повторенням. Маємо
Сполучення з повтореннями. Якщо в сполученнях з n елементів по m деякі з елементів (і навіть всі) можуть виявитися однаковими, то такі поєднання називаються сполученнями з повтореннями із n елементів по m. Число сполучень з повтореннями із n елементів по m позначається символом
Розв’язання. Позначимо Випробуванням є відбір 6 чоловік з 10 акціонерів. Число всіх результатів випробування дорівнює числу сполучень з 10 по 6, тобто
Результатом, що сприяє події А, є відбір шести чоловік серед семи акціонерів, які не мають привілейованих акцій. Число всіх результатів, що сприяють події А, буде Шукана ймовірність
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.139 (0.011 с.) |

 якщо при випробуванні відбувається принаймні одна із цих подій. Множину елементарних подій, що становлять подію А, дістають об’єднанням множин елементарних подій, що становлять події В і С. Аналогічно визначається сума n (n > 2) подій.
якщо при випробуванні відбувається принаймні одна із цих подій. Множину елементарних подій, що становлять подію А, дістають об’єднанням множин елементарних подій, що становлять події В і С. Аналогічно визначається сума n (n > 2) подій. або
або  якщо в результаті випробування відбуваються як подія В, так і подія С. Множина елементарних подій, що становлять подію А, визначається як переріз множин, що становлять події В і С. Аналогічно визначається добуток n (n > 2) подій.
якщо в результаті випробування відбуваються як подія В, так і подія С. Множина елементарних подій, що становлять подію А, визначається як переріз множин, що становлять події В і С. Аналогічно визначається добуток n (n > 2) подій. = {сплата податків одночасно для першого та другого
підприємства}
= {сплата податків одночасно для першого та другого
підприємства}
 , якщо відбувається подія В і не відбувається подія С. Множина елементарних подій, що становлять подію А, містить елементарні події, що становлять В, виключаючи ті, при яких відбувається подія С.
, якщо відбувається подія В і не відбувається подія С. Множина елементарних подій, що становлять подію А, містить елементарні події, що становлять В, виключаючи ті, при яких відбувається подія С.
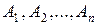 у даному випробуванні утворюють повну групу подій, якщо вони несумісні і в результаті випробування неодмінно відбудеться принаймні одна з них, а отже, їхня сума є достовірною подією.
у даному випробуванні утворюють повну групу подій, якщо вони несумісні і в результаті випробування неодмінно відбудеться принаймні одна з них, а отже, їхня сума є достовірною подією. називаються протилежними, якщо вони несумісні й утворюють повну групу подій, тобто
називаються протилежними, якщо вони несумісні й утворюють повну групу подій, тобто 


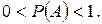
 (1.1)
(1.1) .
. (1.2)
(1.2) .
.
 . Перестановки – не що інше, як спосіб впорядкування якої-небудь кінцевої множини.
. Перестановки – не що інше, як спосіб впорядкування якої-небудь кінцевої множини. (1.3)
(1.3) .
.
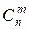 . Воно дорівнює кількості способів, скількома можна витягувати m предметів з n можливих, якщо порядок ролі не грає, і обчислюється за формулою (0 £ m £ n):
. Воно дорівнює кількості способів, скількома можна витягувати m предметів з n можливих, якщо порядок ролі не грає, і обчислюється за формулою (0 £ m £ n): (1.4)
(1.4)
 (1.5)
(1.5) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
 елементів, серед яких один елемент повторюється
елементів, серед яких один елемент повторюється 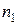 раз, інший елемент повторюється
раз, інший елемент повторюється  раз, і так далі, а останній елемент повторюється
раз, і так далі, а останній елемент повторюється  раз, причому
раз, причому  . Число перестановок з повтореннями позначається
. Число перестановок з повтореннями позначається  та обчислюється за формулою
та обчислюється за формулою (1.6)
(1.6) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
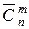 і обчислюється за формулою
і обчислюється за формулою . (1.7)
. (1.7) , що співпадає з результатом приведеного прикладу.
, що співпадає з результатом приведеного прикладу.
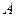 = {серед шести чоловік немає жодного з привілейованими акціями}.
= {серед шести чоловік немає жодного з привілейованими акціями}.

 .
.


