
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості математичного сподіванняСодержание книги
Поиск на нашем сайте 1. 2. 3. 4. Математичне сподівання характеризує середнє значення випадкової величини, навколо якого групуються всі її можливі значення. Дисперсія Дисперсією випадкової величини називається математичне сподівання квадрата різниці випадкової величини та її математичного сподівання:
для дискретної випадкової величини і
для неперервної випадкової величини. Для обчислення
Властивості дисперсії 1. 2. 3. Якщо
Корінь квадратний з дисперсії називається середнім квадратичним відхиленням випадкової величини:
Дисперсія і середнє квадратичне відхилення є мірою розсіювання значень випадкової величини навколо її математичного сподівання
Знайти: Розв’язання. Математичне сподівання
Дисперсію знайдемо за формулою
Середнє квадратичне відхилення
Знайти: а) функцію щільності розподілу; б) математичне сподівання, дисперсію і середнє квадратичне відхилення. Розв’язання. а) за визначенням функції щільності ймовірності
б) Для неперервної випадкової величини
Питання для самоконтролю
1. Дати означення випадкової величини. 2. Які випадкові величини називаються дискретними (неперервними)? Навести приклади. 3. Що називається законом розподілу ймовірностей випадкової величини? 4. Як задаються закони розподілу випадкової величини? 5. Що таке функція розподілу випадкової величини? Навести властивості функції розподілу. 6. Дати означення щільності розподілу ймовірностей неперервної випадкової величини та вказати її властивості. 7. Як обчислюються математичне сподівання, дисперсія і середнє квадратичне відхилення дискретної (неперервної) випадкової величини Х? Навести їх властивості. Завдання 5 5.1. Проводиться перевірка чотирьох банкнот. Скласти закон розподілу числа нефальшивих банкнот. Знайти його математичне сподівання і дисперсію, якщо відомо, що ймовірність того, що банкнота фальшива дорівнює 0,05. 5.2. В об’єднання входять два підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,85, для другого – 0,9. Скласти закон розподілу числа підприємств, що виконали план. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.3. Ймовірність виконання договору для першого підприємства становить 3/5, для другого ця ймовірність становить 4/5. Скласти закон розподілу числа виконаних договорів. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.4. Ймовірність банкрутства для першої фірми дорівнює 0,4 для другої фірми ця ймовірність складає 30%. Скласти закон розподілу числа фірм, що стали банкрутами. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.5. У рекламних цілях торгівельна фірма вкладає в кожну десяту одиницю товару грошовий приз розміром 1 тис. крб. Скласти закон розподілу випадкової величини — розміру виграшу при п'яти зроблених покупках. Знайти математичне сподівання і дисперсію цієї випадкової величини. 5.6. Ймовірність своєчасної сплати податків для першого підприємства дорівнює 0,9, для другого - 0,8. Скласти закон розподілу числа підприємств, що сплатили податки. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.7. Ймовірність повного розрахунку за енергоносії для першого приватного підприємця дорівнює 0,6, для другого - на 50 % більша. Скласти закон розподілу числа підприємців, що сплатили за енергоносії. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.8. Клієнти банку, не зв'язані один з одним, не повертають кредити в строк з ймовірністю 0,1. Скласти закон розподілу числа повернених в строк кредитів з 5 виданих. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.9. Для отримання кредиту підприємець звертається до трьох банків. Ймовірність того, що перший банк не відмовить йому в наданні кредиту, становить 0,6, другий – 0,8. Скласти закон розподілу числа кредитів виданих підприємцю. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини 5.10. Ймовірність своєчасного складання звіту для першого економіста дорівнює 6/7, для другого ця ймовірність дорівнює 7/8. Скласти закон розподілу числа своєчасно складених звітів. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.11. Торгівельна інспекція проводить чотири перевірки торгівельного підприємства на наявність серйозних порушень правил торгівлі. Відомо, що ймовірність виявлення порушення при одній перевірці дорівнює 0,3 і не залежить від результатів попередніх перевірок. Скласти закон розподілу числа виявлених порушень правил торгівлі. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.12. Податкова декларація на прибуток може перевірятися районною або обласною податковою адміністрацією. Ймовірність того, що податкова декларація перевірятиметься обласною адміністрацією – 0,08, районною – 0,06. Рішення щодо перевірки приймаються незалежно. Скласти закон розподілу числа перевірок податкової декларації. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.13. Ймовірність прибуткової діяльності для першої фірми дорівнює 0,8, для другої - 0,7. Скласти закон розподілу числа фірм з прибутковою діяльністю. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини 5.14. В середньому за 10% договорів страхова компанія відшкодовує страхові суми у зв'язку з настанням страхового випадку. Скласти закон розподілу числа таких договорів із навмання вибраних чотирьох. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.15. Знайти закон розподілу числа пакетів акцій, за якими власником буде отриманий прибуток, якщо ймовірність здобуття доходу за кожною з двох придбаних акцій дорівнює відповідно 0,6 та 0,7. Знайти математичне сподівання і дисперсію, середнє квадратичне відхилення цієї випадкової величини. 5.16. Торгівельний агент має 5 телефонних номерів потенційних покупців і дзвонить їм до тих пір, поки не отримує замовлення на покупку товару. Ймовірність того, що потенційний покупець зробить замовлення, дорівнює 0,4. Скласти закон розподілу числа телефонних розмов, які належить провести агентові. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.17. Ймовірність того, що ціна окремої акції зростатиме протягом ділового дня дорівнює 0,4. Природа зміни ціни будь-якого дня є незалежною від того, що сталося попередніми днями. Якщо дослідження проводяться на протязі 3 днів, скласти закон розподілу числа днів, коли акція буде зростати. Знайти математичне сподівання і дисперсію цієї випадкової величини. 5.18. У торгівельного агента є п'ять адрес потенційних покупців, до яких він звертається за списком з пропозицією придбати товар, що реалізовується фірмою. Ймовірність згоди потенційних покупців оцінюється відповідно як 0.5, 0.4, 0.4, 0.3 і 0.25. Покупці приймають рішення про покупку товару незалежно один від одного. Агент звертається до них за вказаним порядком доки хто-небудь з них не погодиться придбати товар. Скласти ряд розподілу випадкової величини X — числа покупців, до яких звернеться агент. Знайти математичне сподівання і дисперсію цієї величини. 5.19. Відділ нагляду відділення центрального банку курирує діяльність ряду комерційних банків. При здачі квартального звіту серйозні фінансові порушення виявляються в середньому в 5% банків. На перевірку обрано три банки. Скласти закон розподілу числа банків з серйозними порушеннями фінансової звітності серед обраних. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини 5.20. Фірма розсилає рекламні проспекти чотирьом потенційним партнерам. В результаті такої розсилки в середньому у кожного п'ятого потенційного партнера виникає інтерес до фірми. Скласти закон розподілу числа партнерів, у яких виникає інтерес до фірми. Обчислити математичне сподівання і дисперсію цієї випадкової величини 5.21. Торгівельна інспекція проводить три перевірки торгівельного підприємства на наявність серйозних порушень правил торгівлі. Відомо, що ймовірність виявлення порушення при одній перевірці дорівнює 0,2 і не залежить від результатів попередніх перевірок. Скласти закон розподілу числа виявлених порушень правил торгівлі. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.22. Ймовірність повного розрахунку за енергоносії для першого заводу дорівнює 0,5, для другого - на 20 % більша. Скласти закон розподілу числа заводів, що не розрахувались за енергоносії. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.23. Із 12 акціонерних товариств 7 успішно функціонують, 3 на межі банкрутства і 2 є банкротами. Громадянин придбав навмання по одній акції 2 акціонерних товариств. Скласти закон розподілу числа куплених акцій товариств, що на межі банкрутства. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.24. Ймовірність повної сплати податків для першого підприємства 4/5, для другого ця ймовірність складає 2/3. Скласти закон розподілу числа підприємств, що повністю сплатили податки. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.25. На курсах підвищення кваліфікації бухгалтерів навчають визначати правильність оформлення накладної. Для перевірки пропонується перевірити 12 накладних, 5 з яких містять помилки. Навмання вибирають дві накладні. Скласти закон розподілу числа накладних, що не містять помилок. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини. 5.26. Ймовірність виконання договору для першого підприємства 2/5, для другого - 0,8, для третього ця ймовірність становить 60 % від суми ймовірностей першого та другого підприємств. Скласти закон розподілу числа підприємств, що виконали договір. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.27. У торгівельного агента є п'ять адрес потенційних покупців, до яких він звертається за списком з пропозицією придбати товар, що реалізовується фірмою. Ймовірність згоди кожного з потенційних покупців оцінюється як 0.4. Покупці приймають рішення про покупку товару незалежно один від одного. Агент звертається до них за вказаним порядком доки хто-небудь з них не погодиться придбати товар. Скласти ряд розподілу випадкової величини X — числа покупців, до яких звернеться агент. Знайти математичне сподівання і дисперсію цієї величини. 5.28. Ймовірність ліквідації заборгованості для першого заводу дорівнює 6/7, для другого - 3/4, для третього - 0,8. Скласти закон розподілу числа заводів, що ліквідували заборгованість. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.29. Ймовірності виконання договору для першого та другого підприємств дорівнюють відповідно 0,8 та 0,7. Скласти закон розподілу числа підприємств, що не виконали договір. Обчислити математичне сподівання і дисперсію цієї випадкової величини. 5.30. В об’єднання входять три підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,8, для другого – 0,9, для третього – 0,85. Скласти закон розподілу числа підприємств, що виконали план. Обчислити математичне сподівання і дисперсію цієї випадкової величини.
Завдання 6
На основі заданої функції розподілу ймовірностей прибутку підприємця потрібно визначити: а) математичне сподівання та середнє квадратичне відхилення прибутку підприємця; б) ймовірність того, що прибуток підприємця набуде значення з інтервалу (а, b):
Значення п, а, b наведені в таблиці. Задачу проілюструвати графічно.
Біноміальний розподіл. Біноміальним називається закон розподілу ймовірностей, що визначаються за формулою Бернуллі
Розв’язання. Випадкова величина Х – число несвоєчасних розрахунків за продукцію – може приймати такі значення
Ряд розподілу
Контроль 0,36 + 0,48 + 0,16 = 1;
Розподіл Пуассона
де
Геометричний розподіл. Дискретна випадкова величина Х має геометричний розподіл з параметром p, якщо вона набуває значень 1, 2,..., m. (нескінченна, але рахункова множина значень) з ймовірністю Ряд геометричного розподілу має вигляд:
Розв’язання. Випадкова величина Х – число перевірених банкнот до виявлення фальшивої має геометричний розподіл з параметром р = 0,05. Розглянемо можливі значення випадкової величини: Тому ряд розподілу має вигляд
Гіпергеометричний закон розподілу. Припустимо є множина N елементів, серед яких М елементів володіють деякою ознакою А. Вибирається випадковим чином без повернення n елементів. Потрібно знайти ймовірність того, що з них m елементів володіють ознакою А. Шукана ймовірність (залежна від N, М, n, m) визначається за формулою Дискретна випадкова величина має гіпергеометричний закон розподілу, якщо вона набуває значень 0, 1, 2, 3, …., m з ймовірностями:
Ряд гіпергеометричного закону розподілу має вигляд:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1047; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 де
де 


 де
де 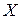 і
і  будь-які випадкові величини.
будь-які випадкові величини.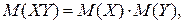 якщо
якщо  та середнє квадратичне відхилення
та середнє квадратичне відхилення 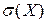
 (2.6)
(2.6) (2.7)
(2.7)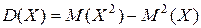 . (2.8)
. (2.8) де
де 


 (2.9)
(2.9)


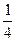


 .
.





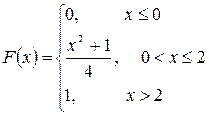





 .
.



 ,
,  ,
,  . (2.10)
. (2.10) Знайдемо ймовірності можливих значень Х:
Знайдемо ймовірності можливих значень Х:





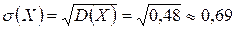
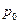

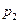


 ,
,  ,
,  ,
,  .
.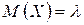 ,
,  ,
,  . (2.11)
. (2.11) , де 0 < p < 1, q = 1 - p.
, де 0 < p < 1, q = 1 - p.



 .
. - перша банкнота фальшива (
- перша банкнота фальшива ( ),
),  - перша дійсна, а друга банкнота фальшива (
- перша дійсна, а друга банкнота фальшива ( ),
),  - перша і друга банкнота дійсна, а третя фальшива (
- перша і друга банкнота дійсна, а третя фальшива ( ), …
), … .
. .
.


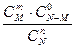
 ,
,  ,
, 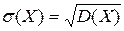 . (2.12)
. (2.12)


