
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теореми додавання та множення ймовірностейСодержание книги
Поиск на нашем сайте
Теорема додавання ймовірностей для несумісних подій. Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій. Р (А+ В)= Р (А)+ Р (В) (1.8) Слідство. Ймовірність суми кінцевого числа попарно несумісних подій дорівнює сумі ймовірностей цих подій.
Розв’язання. Позначимо, що подія А = {витягання червоної кулі з урни}, подія В = {витягання синьої кулі}. Тоді подія А+B – витягання кольорової кулі. Очевидно, що Застосовуючи теорему додавання для несумісних подій, отримаємо: Р (А+ В) = Р(А)+ Р(В)= 0,3+ 0,5= 0,8.
Ймовірність події А, обчислена за умови, що подія В вже відбулася, називається умовною ймовірністю події А і позначається Р (А / В)= PВ(A). Події А і В називаються незалежними, якщо ймовірність однієї з них не зміниться при настанні іншої. Інакше події А і В називаються залежними. Теорема множення ймовірностей. Ймовірність добутку двох подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, тобто Р(АВ) = Р (А) × PА (В) (1.9) Теорема множення для незалежних подій. Ймовірність сумісної появи двох незалежних подій А і В дорівнює добутку ймовірностей цих подій: Р(АВ) = Р(А) × P(В) (1.10) Події називаються незалежними в сукупності, якщо кожна з них і будь-який добуток останніх (що включає або решту всіх подій, або частину з них) є події незалежні. Слідство 1. Ймовірність добутку кінцевого числа незалежних в сукупності подій дорівнює добутку ймовірностей цих подій:
Слідство 2. Ймовірність появи кінцевого числа залежних подій дорівнює
де
Розв’язання. Позначимо події: А = {Здобуття консультаційної роботи в корпорації А }, Р (А)= 0,45; В = {Здобуття консультаційної роботи в корпорації В }, PА (В) = 0,9; Події А і В — залежні, оскільки подія В залежить від того, станеться чи ні подія А. Необхідно знайти ймовірність того, що обидві події (і подія А, і подія В) стануться, тобто Р (АВ). Для цього використовуємо теорему множення ймовірностей (1.9): Р (АВ)= Р (А) PА (В) = 0,45 · 0,9 = 0,405.
Розв’язання. Подія А = {перше узяте випадкове замовлення призначене для внутрішнього вжитку }. Подія В = {друге теж призначене для внутрішнього вжитку}. Нам необхідно знайти ймовірність
Розв’язання. Позначимо події А = {при першому випробуванні з'явиться біла куля}, В = {при другому випробуванні з'явиться чорна куля}, C = {при третьому випробуванні з'явиться синя куля}. Оскільки повинні відбутися всі події, то мова йде про добуток подій АВС. Крім того, події А, В, С залежні, бо друга куля витягується з тих, що залишилися після відбору першої. Ймовірність подій А, В, С визначимо за формулою (1.1). Всього в урні n= 12 куль. Виходячи з умови,
Теорема додавання ймовірностей сумісних подій. Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи. Р (А+ В) = Р(А)+ Р(В) – Р(АВ) (1.13)
Розв’язання. Позначимо А = {прибуток від першої операції}, В = {прибуток від другої операції}. Прибуток буде отриманий від першої, або другої, або від обох операцій, тобто відбудеться подія А+В. Ймовірність отримання прибутку від кожної операції не залежить від результату іншої. Тому події А і В незалежні і сумісні. За теоремою додавання ймовірностей сумісних подій, маємо: Р (А+ В) = Р(А)+ Р(В) – Р(АВ)= 0,8 + 0,7 –
Теорема (ймовірністьпояви принаймні однієї події). Ймовірність появи хоч би однієї з подій
Якщо події
Система подій 1) подія 2) події Сума ймовірностей подій повної групи дорівнює одиниці.
Розв’язання. Позначимо подію А = {повернення хоч би однієї позики}. Знаходимо ймовірність неповернення позики для кожного клієнта:
Яка ймовірність того, що: - усі три знайдуть роботу; - тільки один знайде роботу; - тільки два знайдуть роботу; - не менш як два безробітних знайдуть роботу; - принаймні один. Розв’язання. 1) Подія А = {усі три знайдуть роботу}. Цю подію можна подати як добуток трьох подій
2)Нехай згідно з умовою можуть відбутися події Подія В = {тільки один із трьох безробітних знайде роботу}. Цю подію можна подати так:
3) Подія С = {тільки два із трьох безробітних знайдуть роботу}. Подамо цю подію через події
Подію С подано як суму несумісних груп подій. У кожній групі події незалежні. Знайдемо ймовірність події С:
4) Нехай подія D = {серед трьох безробітних не менш як два знайдуть роботу}. Тоді її можна подати як суму двох подій:
5) Подія К = {із трьох безробітних принаймні один знайде роботу}. Протилежна подія - «усі три безробітних не знайдуть роботу». Ймовірність цієї події або
Питання для самоконтролю 1. Сформулювати теореми додавання ймовірностей для несумісних і сумісних подій. 2. Які випадкові події називаються: а) незалежними в сукупності; б) попарно незалежними? 3. Дати означення умовної ймовірності випадкової події. 4. Сформулювати теореми множення ймовірностей для залежних і незалежних подій. 5. Записати формулу обчислення ймовірності появи принаймні однієї з п несумісних подій. Завдання 2 2.1. Для отримання кредиту підприємець звертається до двох банків. Ймовірність того, що перший банк не відмовить йому в наданні кредиту, становить 0,7, другий – 0,85. Знайти ймовірність того, що: а) перший або другий банк дасть згоду на кредитування; б) обидва банки відмовляться надати кредит. 2.2. Ймовірність того, що ціна окремої акції зростатиме протягом ділового дня дорівнює 0,4. Якщо природа зміни ціни будь-якого дня є незалежною від того, що сталося попереднього дня (днів), то яка ймовірність того, що ціна: а) зростатиме чотири дні підряд? б) зростатиме два з трьох днів? 2.3. З партії виробів товарознавець навмання відбирає вироби вищого сорту. Ймовірність того, що вибрана річ виявиться вищого сорту дорівнює 0,8; першого сорту – 0,7; другого сорту – 0,5. Знайти ймовірність того, що з трьох наугад відібраних виробів будуть: а) лише два вищого сорту; б) всі різні. 2.4. У двох із 14 складених касиром рахунків є помилки. Ревізор вирішив перевірити навмання 5 рахунків. Яка ймовірність, що помилки будуть виявлені менш ніж в двох? 2.5. Два бухгалтери обробляють рівну кількість рахунків. Ймовірність того, що перший бухгалтер допустить помилку, дорівнює 0,005, для другого ця ймовірність дорівнює 0,01. Знайти ймовірність того, що при перевірці рахунків: а) лише перший бухгалтер допустив помилку; б) помилки допущені не були. 2.6. Податкова декларація на прибуток може перевірятися районною або обласною податковою адміністрацією. Ймовірність того, що податкова декларація перевірятиметься обласною адміністрацією – 0,05, районною – 0,04. Рішення щодо перевірки на обласному і районному рівнях приймаються незалежно: а) яка ймовірність бути перевіреним обома адміністраціями? б) яка ймовірність пройти тільки районну перевірку? в) яка ймовірність не бути перевіреним? 2.7. Ймовірність отримати прибуток з акцій компаній А, В і С для акціонера відповідно дорівнюють 0,6; 0,7; 0,5. Знайти ймовірність того, що: а) лише один вид акцій складе прибуток акціонера, б) хоча б один вид акцій принесе прибуток їх володареві. 2.8. Ймовірність банкрутства для першої фірми - це додатний розв’язок рівняння 2.9. Ймовірність своєчасної сплати податків для першого підприємства дорівнює 0,8, для другого - 0,6, для третього - 2/3. Визначити ймовірність своєчасної сплати податків а) не більше ніж одним підприємством; б) тільки одним підприємством. 2.10. В об’єднання входять три підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,8, для другого – 0,9, для третього – 0,85. Знайти ймовірність таких подій: а) договір виконає лише одне підприємство; б) договір виконають всі підприємства. 2.11. Ймовірність прибуткової діяльності для першої фірми дорівнює 0,7, для другої - 0,5, для третьої ця ймовірність у три рази менша від суми ймовірностей для першої та другої фірм. Знайти ймовірність того, що прибутковими будуть а) дві фірми; б) хоча б одна фірма. 2.12. На курсах підвищення кваліфікації бухгалтерів навчають визначати правильність оформлення накладної. Для перевірки викладач пропонує перевірити 12 накладних, 5 з яких містять помилки. Навмання вибирають три накладних. Яка ймовірність того, що з трьох накладних не менше двох з помилками? 2.13. Надійність першого банку – 0,95; для другого – 0,8; для третього – 0,85. Підприємець зробив вклад в усі три банки. Знайти ймовірність того, що підприємцеві повернуть вклад: а) два банки; б) хоча б один банк. 2.14. Ймовірність виконання договору для першого підприємства становить 3/5, для другого ця ймовірність є розв’язком рівняння 2.15. Ймовірність повного розрахунку за енергоносії для першого заводу дорівнює 0,5, для другого - на 20 % більша. Знайти ймовірність своєчасної сплати за енергоносії: а) одним заводом; б) двома заводами. 2.16. Ймовірність виконання договору для першої фірми є розв’язком рівняння 2.17. Ймовірність повної сплати податків для першого підприємства 4/5, для другого ця ймовірність задовольняє рівнянню 2.18. Ймовірність банкрутства для першої фабрики дорівнює 0,2, для другої - на 50 % більша ніж для першої, для третьої дана ймовірність є розв’язком рівняння 2.19. Ймовірність виконання договору для першого підприємства 2/5, для другого - 0,8, для третього ця ймовірність становить 60 % від суми ймовірностей першого та другого підприємств. Знайти ймовірність виконання договору тільки двома підприємствами. 2.20. Ймовірність того, що в певний день торгівельній базі буде потрібна двухтонна машина, дорівнює 0,9, п'ятитонна – 0,7. Визначити ймовірність того, що торгівельній базі буде потрібна: а) двухтонна і п'ятитонна машина; б) жодна з них; в) хоча б одна автомашина. 2.21. Перша фірма може одержати заданий прибуток з ймовірністю 0,7, для другої ця ймовірність є розв’язком рівняння 2.22. Ймовірність ліквідації заборгованості для першого заводу дорівнює 6/7, для другого - 3/4, для третього - 0,8. Знайти ймовірність ліквідації заборгованості хоча б двома заводами. 2.23. Ймовірність того, що податкова інспекція пред'явить штраф першому підприємству – 0,2, другому – 0,3, третьому – 0,15. Знайти ймовірність того, що будуть оштрафовані: а) три підприємства; б) два підприємства. 2.24. Технологічний процес складається з декількох операцій. Ймовірність того, що під час першої операції виріб отримає пошкодження, дорівнює 0,1, а під час другої операції – 0,05. Яка ймовірність того, що після двох операцій виріб виявиться а) пошкодженим; б) непошкодженим? 2.25. Банк може видати кредит одному з трьох клієнтів з ймовірністю 2.26. Ймовірність своєчасного складання звіту для першого економіста дорівнює 0,9, для другого ця ймовірність є додатним коренем рівняння 2.27. Заводом відправлена автомашина за різними матеріалами на чотири бази. Ймовірність наявності потрібного матеріалу на першій базі дорівнює 0,9, на другій – 0,95, на третій – 0,8, на четвертій – 0,6. Знайти ймовірність того, що лише на одній базі не виявиться потрібного матеріалу. 2.28. Ймовірності своєчасного повернення кредитів кожним з трьох позичальників банку відповідно дорівнюють: 0,6; 0,9; 0,7. Знайти ймовірність наступних подій: а) лише два позичальники повернуть кредит своєчасно; б) хоча б один з позичальників поверне кредит своєчасно. 2.29. Ймовірності виконання договору для першого та другого підприємств задовольняють системі рівнянь Знайти ймовірність виконання договору тільки одним підприємством. 2.30. В об’єднання входять три підприємства. Ймовірність виконати план для першого підприємства дорівнює 0,8, для другого – 0,9, для третього – 0,85. Знайти ймовірність таких подій: а) договір виконують 2 підприємства; б) договір не виконає жодне підприємство.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1738; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.007 с.) |

 ,
,  .
. (1.11)
(1.11) , (1.12)
, (1.12) – ймовірність події
– ймовірність події  за умови, що
за умови, що  .,
.,  вже настали. Відмітимо, що порядок розташування подій може бути будь-яким.
вже настали. Відмітимо, що порядок розташування подій може бути будь-яким. Тоді за теоремою множення ймовірностей залежних подій маємо
Тоді за теоремою множення ймовірностей залежних подій маємо .
. . Оскільки одну кулю вийняли, то в урні залишилося 11 куль і
. Оскільки одну кулю вийняли, то в урні залишилося 11 куль і  . Аналогічно
. Аналогічно  . За теоремою множення ймовірностей отримаємо:
. За теоремою множення ймовірностей отримаємо: .
. = 0,94.
= 0,94. ,…,
,…,  ,
,  ,…,
,…, 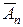
 (1.14)
(1.14)
 ,
,  ,…,
,…,  називається повною групою подій для даного випробування, якщо будь-яким його результатом є одна і лише одна подія цієї групи. Іншими словами, для повної групи виконуються умови:
називається повною групою подій для даного випробування, якщо будь-яким його результатом є одна і лише одна подія цієї групи. Іншими словами, для повної групи виконуються умови: достовірна;
достовірна; і
і  (i ¹ j) попарно несумісні.
(i ¹ j) попарно несумісні. ;
;  ;
;  . Знайти ймовірність повернення хоча б однієї позики.
. Знайти ймовірність повернення хоча б однієї позики.
 ;
;  ;
;  . Застосовуючи формулу (1.14), отримаємо:
. Застосовуючи формулу (1.14), отримаємо:  .
. де і -тий безробітний знайде роботу. Ймовірність події А обчислюємо так:
де і -тий безробітний знайде роботу. Ймовірність події А обчислюємо так:
 , які полягають відповідно в тому, що перший, другий і третій безробітні знайдуть роботу.
, які полягають відповідно в тому, що перший, другий і третій безробітні знайдуть роботу.
 Групи подій, сумою яких є подія В, несумісні між собою, а події в кожній групі незалежні. Тому ймовірність події В обчислимо так:
Групи подій, сумою яких є подія В, несумісні між собою, а події в кожній групі незалежні. Тому ймовірність події В обчислимо так:
 та протилежні до них:
та протилежні до них:

 = {серед трьох безробітних два знайдуть роботу і один не знайде} і А = {усі три знайдуть роботу}.Тому маємо:
= {серед трьох безробітних два знайдуть роботу і один не знайде} і А = {усі три знайдуть роботу}.Тому маємо:

 .
. для другої фірми ця ймовірність на 25 % більша. Знайти ймовірність того, що із двох фірм збанкрутує: а) лише одна, б) хоча б одна.
для другої фірми ця ймовірність на 25 % більша. Знайти ймовірність того, що із двох фірм збанкрутує: а) лише одна, б) хоча б одна. Визначити ймовірність виконання договору: а) одним підприємством; б) хоча б одним підприємством.
Визначити ймовірність виконання договору: а) одним підприємством; б) хоча б одним підприємством. , для другої ця ймовірність дорівнює 0,8. Яка ймовірність виконання договору не більше ніж однією фірмою? Обома фірмами?
, для другої ця ймовірність дорівнює 0,8. Яка ймовірність виконання договору не більше ніж однією фірмою? Обома фірмами? . Знайти ймовірність повної сплати податків одним підприємством.
. Знайти ймовірність повної сплати податків одним підприємством. . Визначити ймовірність банкрутства тільки однієї фабрики.
. Визначити ймовірність банкрутства тільки однієї фабрики. Визначити ймовірність одержання заданого прибутку: а) принаймні однією фірмою, б) тільки однією фірмою.
Визначити ймовірність одержання заданого прибутку: а) принаймні однією фірмою, б) тільки однією фірмою. відповідно. Знайти ймовірність того, що кредит отримає: а) лише один клієнт; б) усі клієнти.
відповідно. Знайти ймовірність того, що кредит отримає: а) лише один клієнт; б) усі клієнти. Яка ймовірність несвоєчасного складання звіту двома економістами.
Яка ймовірність несвоєчасного складання звіту двома економістами.



