
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Складання структурно-логічної формулиСодержание книги
Поиск на нашем сайте
Структурно-логічна формула визначає взаємозв'язок імовірностей забезпечення pecypciв складальних одиниць з імовірністю забезпечення ресурсу автомобіля в цілому. Основою для складання розрахункового рівняння є структурна схема надійності виробу. На структурой cxeмi вci комплекти з'єднані між собою послідовно. 3 теорії ймовірностей відомо, що при послідовному з'еднанні елементів (у даному paзi ремонтних комплектів) імовірність безвідмовної роботи об'єкта дорівнює добутку ймовірностей безвідмовної роботи цих елементів (комплектів), тобто на підставі теореми множення ймовірностей можна записати:
Для вcix складальних одиниць, крім істотно малих величин, які входять до структурної схеми, добирають значення ймовірностей роботи їх без капітального ремонту за умови забезпечення заданого гамма-відсоткового ресурсу автомобіля Р(Трγ) та забезпечення гамма-відсоткового ресурсу кожної складальної одиниці. 3 теорії надійності відомо, що ймовірність роботи складальних одиниць без капітального ремонту за період напрацювання Тру є регламентованою величиною Ймовірності забезпечення заданого ресурсу:
Для автомобіля в цілому формулу (8) на підставі формули (7) можна записати:
де к — кількість комплектів; γ — iмовірність забезпечення заданого напрацювання Тр до першого капітального ремонту, %. Для автомобілів γ Для базових складальних одиниць, які на cxeмi з’єднані n ос л i д о в н о, беруть добуток цих імовірностей: Р = Р1 Р2…Рк Імовірність складальних одиниць, що мають істотно малі ранги Ri<<а, які стоять під стрілкою, в розрахунковій формулі не враховують, а ранги 1 > Для ремонтних комплектів з паралельними з’єднаннями елементів у структурній cxeмi імовірність працездатного стану комплекту залежить від iмовірності працездатного стану кожної iз складальних одиниць цього комплекту. 3 тeopiї ймовірностей відомо, що надійність роботи паралельно з'єднаних елементів (тобто ймовірність того, що хоч би один з них працюватиме) дорівнюватиме cyмi ймовірностей ycix можливих сприятливих наслідків. Для двох елементів, з'єднаних паралельно, вci можливі стани працездатності можна записати так: • нi елемент А, ні елемент Б не вийдуть з ладу; • елемент А вийде з ладу, а елемент Б виявиться працездатним; • елемент Б вийде з ладу, а елемент А виявиться працездатним. Математично це можна записати так:
У разі трьох паралельно з'єднаних елементів А, Б працездатних станів різко збільшується:
Як видно з останньої piвноcтi, такий запис при збільшенні кількості паралельно з'єднаних елементів стає громіздким. Тому ймовірність безвідмовної роботи P(t) в цьому paзi спробуємо записати через імовірність відмови Q (t). Для того щоб такий комплект перебував у стані відмови, треба, аби одночасно відмовили вci його елементи, оскільки якщо хоч одна складальна одиниця працюватиме, то працюватиме i весь комплект. Позначимо ймовірність відмови складальної одиниці (деталі) — qi, імовірність відмови всього комплекту – Q. Тоді, згідно з теоремою множення ймовірностей:
(10) При q1 = q2 = q3= q4 формулу (10) можна записати так:
Відомо, що сума ймовірностей відмови та ймовірностей безвідмовної роботи, тобто сума протилежних noдій, дорівнює одиниці:
звідки
(13) Тоді на підставі формул (11) та (13) можна записати:
звідки
(15)
(16)
де n – кількість складальних одиниць у комплекті. На підставі формули (16) імовірність комплекту з трьох паралельно з’єднаних одиниць (рис. 1.1, в):
Для складальних одиниць комплекту третього типу, тобто паралельно-послідовних складальних одиниць, визначають імовірність безвідмовної роботи кожного з комплектів з паралельним з’єднанням, а розрахунок ведуть так само, як і для послідовно з’єднаних уже розглянених комплектів. Для структурно-логічної схеми (див. рис. 1, г) можна записати
Імовірність складальних одиниць, що розміщені під стрілкою, в цих комплектах у розрахунковій формулі не враховують. Для структурної схеми (рис. 1) розрахункова формула має вигляд:
Відомо, що для автомобіля в цілому γ =80%. Для того щоб виконати ці вимоги, треба задатися значеннями ймовірностей роботи без капітального ремонту з кожної складальної одиниці так, аби Р(Тру)
(20) Тобто:
Отже, висунута вимога за величиною γі, для складальних одиниць задовольняє поставлену умову. Якщо в результаті розрахунку за складеною на підставі структурної схеми i прийнятим значенням імовірностей нерівність Р(Тру) > γ/100 не задовольняється, слід відповідно збільшити або зменшити прийняті значення ймовірностей Рі для одного або кількох послідовних елементів схеми, після чого повторити обчислення. Якщо капітальний ремонт виробу не передбачено i ресурс задається до списання, то перед складанням структурної схеми слід описати граничні стани автомобіля, що обумовлюють необхідність списання. Отже, якщо ставиться завдання: за весь ресурс автомобіля, що складається, наприклад, з десяти складальних одиниць, з імовірністю 0,8 не проводити жодного капітального ремонту будь-якої складальної одиниці, то вci складальні одиниці (вузли) стають базовими i в цьому paзi для забезпечення висунутих вимог треба, щоб кожна з них мала ресурс з імовірністю забезпечення не менш як 0,98. Тоді Р(Тру) = 0,9810 = 0,817 > 0,8. Якщо виріб складається з п'яти складальних одиниць, то необхідно, щоб кожна з них мала ресурс з імовірністю забезпечення не менш як 0,95, оскільки:
Отже, чим складніший автомобіль, тим вищими стають вимоги до імовірності забезпечення заданого ресурсу. Розглянуті приклади розкривають універсальність запропонованих структурних схем, які відбивають різноманітність вимог до надійності автомобілів piзнoгo класу та призначення i перетворюють вихідну інформацію на нову зi своєю внутрішньою структурою (організацією). Як інформаційно-логічна система структурна схема надійності здатна відображати i перетворювати як вимоги до ремонтопридатності та довговічності (якщо висувається критерій граничного стану автомобіля в будь-якому його виявленні), так i вимоги до безпеки (якщо критерію граничного стану немає, а важливим є лише факт наявності відмови проектованого автомобіля).
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.247 (0.006 с.) |



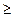 80 %. Така сама умова має виконуватися для кожної складальної одиниці. Вищі значення беруть для базових одиниць i металоконструкцій. Для відповідальних складальних одиниць, надійність роботи яких пов’язана з безпекою людини (наприклад, гальм), треба брати максимальне значення γ (99%) незалежно від рангу ремонтних затрат і розміщення складальної одиниці в структурній схемі. Значення ймовірностей складальних одиниць (деталей), що входять до і -го комплекту, обчислюють залежність від виду з’єднання їх у комплекті.
80 %. Така сама умова має виконуватися для кожної складальної одиниці. Вищі значення беруть для базових одиниць i металоконструкцій. Для відповідальних складальних одиниць, надійність роботи яких пов’язана з безпекою людини (наприклад, гальм), треба брати максимальне значення γ (99%) незалежно від рангу ремонтних затрат і розміщення складальної одиниці в структурній схемі. Значення ймовірностей складальних одиниць (деталей), що входять до і -го комплекту, обчислюють залежність від виду з’єднання їх у комплекті. , які знаходяться в комплекті з істотно малими рангами, записують у формулі послідовно з рангами
, які знаходяться в комплекті з істотно малими рангами, записують у формулі послідовно з рангами 

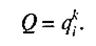 (11)
(11) ((12)
((12)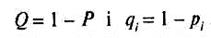
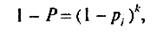 (14)
(14)
 Застосовуючи теорему множення та знак добутку, можна записати:
Застосовуючи теорему множення та знак добутку, можна записати: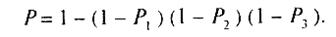 (17)
(17) (18)
(18) (19)
(19) 0,8.
0,8.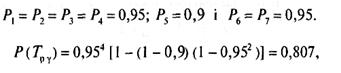 Нехай:
Нехай: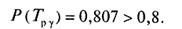 (21)
(21)



