
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок імовірності неруйнування валів та осейСодержание книги
Поиск на нашем сайте
За критерієм міцності від втомленості За умов стаціонарного режиму навантаження при згинанні
Вали та осі розраховують для кожного місця концентрації напружень. Розрахунок зводиться до визначеня ймовірностей неруйнування місця концетрації та ймовірності неруйнування валу для m концентрацій напружень, нормального розподілу ресурсу та середньої границі витривалості валу, сумарного коеційнту варіації витривалості валу. Розрахуноква ймовірність неруйнування валу для m концентраторів напружень визначається наступним чином:
де Р(Трγ) – імовірність неруйнування j-ї деталі (валу) протягом заданого гамма-відсоткового ресурсу; Qк(Nц) – ймовірність руйнування місця концентрацї напруження при заданому циклі навантаження вала, що відповідають заданому ресурсу.
Кількість циклів навантаження валу до руйнування (в навчальних цілях видається згідно індивідуального завдання викладачем): Nц = 60nTрγ (29) де n – частота обертання, хв-1 Трγ – заданий гамма-відсотковий ресурс вала, год
Значення ймовірності неруйнквання вала має задовольняти умову: 100Р(Тру) Р(Трγ) – задана ймовірність неруйнування вала (γj=90%). Величину Qк(Nц) визначають згідно знайденого значення квантиля нормального розподілу:
де nз – безрозмірна величина (умовний коефіцієнт запасу витривалості валу), Vσ-1q, та Vσв – коефіцієнти варіації. Значення Vσв, коли нема експериментальних даних, приймають 0,3÷0,5. Сумарний коефіцієнт
де К – коефіцієнт допустимого перевищення границі витривалості, що залежить від кількості циклів Nц до руйнування валу (вибирається з таблиці 5.1). σ-1q – середня границя витривалості вала при згинанні, кПа; σа – середнє значення амплітуди циклу навантаження, кПа; Таблиця 5.1 Значення коефіцієнта К залежно від кількості циклів навантаження Nц
Сумарний коефіцієнт варіації витривалості вала розраховують за наступною формулою:
де Δ – однобічний допуск на виготовлення місця концентрації (видається згідно індивідуального завдання), мм ρ – радіус гальтелі, виточки або іншого якого-небудь концентратора напруження, мм
Середня границя витривалості вала при згинанні визначається наступним чином:
при крученні:
де ασ, ατ – теоретичні коефіцієнти концентрації напружень відповідно при згинанні та при крученні (рис. 5.1 – 5.4); Uσ, Uτ – нижні межі границі витривалості матеріалу вала відповідно при згинанні та при крученні, Мпа; АLσ, АLσ – сталі величини відповідно при згинанні та крученні; L – периметр малого уступу (L=πd), мм; σ, στ - відносний градієнт першого головного напруження в місці концентрації напружень відповідно при згинанні та крученні.
Рис. 5.1 – Теоретичні коефіцієнти концентрації напружень ασ та ατ для валів із кільцевою виточкою при крученні (а) і згинанні (б)
Рис. 5.2 - Теоретичні коефіцієнти концентрації напружень ασ та ατ для ступінчастих валів з галтеллю при крученні (а) й згинанні (б)
Рис. 5.3 - Теоретичні коефіцієнти концентрації напружень ασ та ατ для валів з поперечним отвором при крученні й згинанні. Значення Uσ, Uτ, що входять до виразів 34, 35, обчислюють відповідно за наступними формулами:
Сталі величини В, АLσ та АLτ розраховуються відповідно наступним чином:
Значення відносних градієнтів σ та στ залежать від типу ослабленості перерізу валу (наявності галтелі, кільцевої канавки, шліців чи шпонкового пазу).
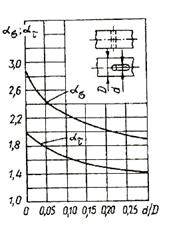
Рис. 5.4 - Теоретичні коефіцієнти концентрації напружень ασ та ατ для валів з шпонковим пазом при крученні й згинанні.
Для валу із галтеллю: при згинанні при крученні де r – радіус галтелі, виточки чи іншого концентратора напруження, мм; d – діаметр меншого уступу валу або внутрішній діаметр шліців, мм; Для валу з кільцевою канавкою: при згинанні при крученні Для вала із шліцевою канавкою чи шпонковим пазом: при згинанні при крученні Периметр малого уступу валу визначається за на ступною формулою:
Приклад розрахунку Завдання. Розрахувати ймовірність неруйнування валу за критерієм міцності від втомленості. Вал має: шпонковий паз. Згинальний момент Мзг=10 Нм. Кількість циклів навантаження вала до руйнування Матеріал: Сталь 45. Гамма відсотковий-ресурс вала Ескіз вала:
Конструктивні розміри вала:
Послідовність розрахунку
1. Визначаємо нижню межу границю витривалості матеріалу вала при згинанні
де, σв – межа міцності відповідного матеріалу (вибирається залежно від матеріалу вала) σв=61 кг=610 Н. 2. Розраховуємо сталу В:
3. Обчислюємо сталу А при згинанні: АLσ=10*В=1.35 4. Знаходимо Теоретичний коефіцієнт концентрації напружень α G залежно від співвідношення r/d. ασ=r/d=0.0125 5. Визначаємо периметр малого уступу вала L: L=π*d=3.14*100=314 6. Розраховуємо відносний градієнт напруження σ: σ=(2/d)+3=3.02H 7. Визначаємо середню границю витривалості G-1q при згинанні: σ-1q = 8. Визначаємо коефіцієнт допустимого переміщення границі витривалості К=1.13, залежно від кількості циклів до руйнування Nц за таблицею 14.10 [1 ст. 238]. 9.Розраховуємо умовний коефіцієнт запасу вала nз. nз = де, σamax = 100000— значення амплітуди навантаження σamax=Mзг/Wзг=100000 МПа Мзг = 10 Н*м – згинальний момент; Wзг =
10. Обчислюємо сумарний коефіцієнт варіації
де, 11. Визначаїмо кванти нормального розподілу Uq:
де, Vσa =0,3 – коефіцієнт варіації. 12. Знаходимо значення імовірності не руйнування місця концентрації
13. Перевіряємо виконання умови:
Висновок: Умова про не руйнування вала при згинанні на заданих умовах навантаження виконується. В разі, коли умова не виконується, необхідно виконати наступне: 1- Перевірити кількість циклів 2- Збільшити коефіцієнт α σ (для цього потрібно збільшити конструктивні розміри d, r, b) або зменшити. 3. Взяти більш міцний матеріал з більшим значенням σв.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.41.108 (0.006 с.) |

 (28)
(28) , γj(30)
, γj(30)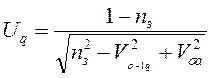 (31)
(31) (32)
(32) (33)
(33) (34)
(34) (35)
(35)

 ,
, 
 ;
; ;
; ;
;
 ;
;
 ;
;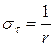
 ;
;


 год, при γ=90%.
год, при γ=90%.
 мм, d=100 мм, b=10 мм.
мм, d=100 мм, b=10 мм. Н
Н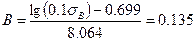

 =0,13
=0,13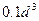 =0,0001 — момент опору перерізу вала при згинанні.
=0,0001 — момент опору перерізу вала при згинанні.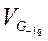 :
:
 мм
мм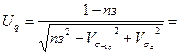 2.9
2.9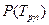 [1, ст.374].
[1, ст.374]. . Може їх потрібно зменшити
. Може їх потрібно зменшити  коректуємо
коректуємо 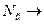 0.
0.


