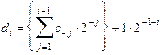Алгоритм извлечения квадратного корня операнда с плавающей запятой

 

Есть два способа аппаратной реализации процедуры извлечения квадратного корня. Первый способ связан с разработкой микропрограммы извлечения квадратного корня, основанной на использовании основных арифметических операций и являющейся реализацией того или иного итерационного метода извлечения квадратного корня. Другой путь состоит в создании алгоритма извлечения квадратного корня сходного по структуре с алгоритмами основных арифметических действий. Предполагается, что второй вариант алгоритма выполняется быстрее, но он обычно требует достаточно существенного усложнения блока управления арифметического устройства цифрового автомата.

Рассмотрим второй способ организации алгоритма извлечения квадратного корня только положительного операнда в форме с плавающей запятой, который загружается в регистр AC.

Перед началом процедуры проводится проверка знака операнда и его величины на ноль.

Очевидно, что процедура извлечения квадратного корня в этом случае распадается на две операции: извлечение квадратного корня из характеристики числа и из мантиссы. Первая операция достаточно тривиальна. Если характеристика числа четная, то ее делят на два, т.е. выполняется процедура [AC(CH)]. Если же характеристика нечетная, то выполняется один шаг денорализации: [AC(FR)] и [AC(CH)] _ 1\ Потом характеристика делится на два. В обоих случаях окончательный результат засылается в MQ(CH), т.к. в регистре MQ формируется результат извлечения квадратного корня.

Весь процесс извлечения кадратного корня из мантиссы операнда разбивается на ряд однотипных шагов, выполняемых последовательно, и на каждом шаге находится очередная цифра результата, начиная со старшей. Этот алгоритм очень похож на обычный алгоритм деления, за тем исключением, что на каждом очередном шаге реализации алгоритма все время меняется "делитель", который формируется в регистре SR из текущего значения результата извлечения квадратного корня. Окончательный результат получается за m -1 элементарных шагов алгоритма или же после того шага, на котором очередной остаток получился равнм нулю.

Значение очередной цифры результата определяется вычитанием из остатка (на первом шаге остаток - это подкоренное число!) специально сформированного "делителя". Как уже отмечалось, результат извлечения корня из мантиссы операнда формируется в субрегистре MQ(FR), а очередное значение "делителя" форимируется в субрегистре SR(FR).

На первом шаге алгоритма (i = 1)"делитель" (d) равен 12-1-i, т.е. 0.01.

На втором шаге d = ci-12-(i-1)+ 12-(1 + i) = {c12-1} + 12-3.

На третьем шаге d = c12-1+ ci-12-(i-1)+ 12-(1 + i) = {c12-1+ c22-2} + 12-4

и т.д.

Фигурными скобками выделен очередной результат извлечения квадратного корня, полученный на текущем шаге алгоритма.

Здесь ci-1-значение цифры очередного разряда результата, полученного на i-том шаге алгоритма. Само же значение цифры определяется на (i-1)-том шаге. Если результат вычитания из остатка положителен, то для следующего шага алгоритма ci-1 = 1, если же результат отрицателен, то ci-1 = 0.

В общем виде значение "делителя" на i -том шаге деления можно представить следующим образом:

 

Как уже отмечалось, фигурными скобками выделено формируемое значение результата извлечения квадратного корня.

Рассмотрим детально алгоритм извлечения квадратного корня из некоторого числа A = rAmA представленного в форме с плавающей запятой. Здесь rA - характеристика числа, mA - мантисса.

В этом алгоритме последовательно выполняются следующие процедуры.

1. 0 TQ, F FC| mA AC(FR), rA AC(CH). Если А < 0 или А = 0, то конец процедуры извлечения корня квадратного: переход к п.14. В первом случае фиксируется ошибка: 1 TQ\

2. 0 MQ, 0 SR, m SC, 0 AC(QFR).

3. Если [AC(CH)] нечетно, то [AC(FR)], AC(CH):= [AC(CH)] _ 1\

4. [AC(CH)], [AC(CH)] MQ(CH).

5. 1 SR([SC] _ 1)\

6. AC(QFR,FR):= [AC(QFR,FR)] _ [SR(S,FR)], если [AC(QFR,FR)] = 0, то переход к п.13, иначе переход к п.7.

7. Если QFR = 0= то 1 MQ([SC]) и переход на п.8, иначе переход на п.9.

8. Если AC(FR) = 0, то переход к п. 13, иначе переход к п. 10.

9. 0 MQ([SC]), AC(FR):= [AC(QFR,FR)] + [SR(FR)].

10. SC:= [SC] _ 1, [AC(FR)].

11. Если [SC] = 0, то переход к п. 13, иначе переход к п.12.

12. [MQ(FR)] SR(FR) и переход к п. 5.

13. Если [AC(m)] = 0= то выполняется обычная процедура нормализации. В любом случае после п.13 происходит переход к п. 14.

14. Конец процедуры извлечения квадратного корня.

Совокупность процедур от пункта 5 до пункта 12 включительно составляет элементарный шаг алгоритма.

Граф-схема алгоритма извлечения квадратного корня приведена на

рис. 11.17.

Блок управления АУ, предназначенного не только для выполнения основных арифметических действий с операндами в форме с плавающей запятой, но и выполняющего процедуру извлечения квадратного корня, должен обеспечить передачу содержимого из MQ(FR) и SR(FR), ввод 1 в разряд регистра SR с номером равным значению [SC] - 1 и ввод 1 или 0 в разряд регистра MQ с номером равным [SC]. В АУ предусматривается дополнительный триггер TQ для фиксации ошибки при выполнении алгоритма извлечения квадратного корня.

В данном алгоритме выполняется процедура восстановления остатка. В принципе можно разработать алгоритм извлечения квадратного корня и без процедуры восстановления остатка.

 

 

Рис. 11.17.

 

Приложение

 

Определения основных понятий и терминов

 

Информация - это сведения обопределенных свойствах или параметрах тех или иных явлений или объектов и о зависимостях между этими свойствами.

 

Сообщение - это информация, воплощенная и зафиксированная в некоторой материальной форме.

 

Сигнал - это физическое средство передачи сообщения. Или иначе: сигнал - это процесс изменения во времени некоторого физического параметра s(t) какого-либо объекта, служащий для отображения, регистрации и передачи сообщения.

 

Типы сигналов: аналоговый, дискретный, квантованный, оцифрованный (кодированный), модулированный, импульсный и т.д.

 

Интерфейс - это совокупность аппаратных и программных средств для организации информационной связи между информационными устройствами, т.е. устройствами, осуществляющими прием, передачу, хранение информации и ее обработку.

 

Система счисления - это совокупность приемов и правил для записи чисел цифровыми знаками.

 

Непозиционная система счисления - это система, для которой значение символа, т.е. цифры, не зависит от его положения в числе.

 

Позиционная система счисления - это система, в которой значение каждой цифры зависит не только от ее числового эквивалента, но и от ее места (позиции) в числе, т.е. один и тот же символ (цифра) может принимать различные значения.

 

Основание или базис q позиционной системы счисления - это количество знаков или символов, используемых для изображения числа в данной системе. В частности, различают десятичную (q = 10), двоичную (q = 2), восьмеричную (q = 8) и шестнадцатеричную (q = 16) позиционные системы счисления.

 

Код числа - это запись числа в некоторой системе счисления. Например, двоичный код, десятичный, восьмеричный и т.д.

 

Длина разрядной сетки - число разрядов (позиций), выделяемых в компьютере для представления числа в позиционной системе счисления (в основном в двоичной системе).

 

Вес разряда числа в позиционной системе счисления - это величина P i = q i, где i - номер разряда разрядной сетки, отсчитываемый справа налево.

 

Длина числа (слова) - это количество позиций (или разрядов) в записи числа.

 

Бит - один разряд (одна позиция) в двоичной системе счисления.

 

Байт - восемь битов.

 

Диапазон представления чисел в заданной системе счисления - это интервал числовой оси, заключенный между максимальным и минимальным числами, значение которых зависит от длины разрядной сетки, выделенной в машине для представления чисел.

 

Машинное (автоматное) изображение числа - это представление числа в разрядной сетке компьютера.

 

Форма представления двоичных чисел в компьютере. Различают две основные формы представления: с фиксированной запятой (точкой) и с плавающей запятой.

 

Фиксированная запятая (точка) - машинная форма представления целых чисел или правильной дроби. Разрядная сетка, выделенная для представления числа в этой форме, разбивается на две части: старший разряд выделяется под знак числа, а в остальной части (в поле числа) представляется значение числа. Для целых чисел запятая фиксируется правее младшего разряда, а для правильной дроби - левее старшего разряда поля числа.

 

Формы представления отрицательных чисел с фиксированной запятой:

прямой код - значение модуля числа представляется в обычном двоичном коде;

обратный код - все разряды значения числа, представленного в прямом коде, инвертируются;

дополнительный код - к значени. числа, представленного в обратном коде, прибавляется единица.

Во всех случаях в знаковый разряд отрицательного числа записывается единица.

 

Плавающая запятая (точка) - машинная форма представления вещественных чисел. Разрядная сетка, выделенная для представления числа в этой форме, разбивается на три части: старший разряд обычно выделяется под знак числа, следующие n p разрядов под порядок (или храктеристику) числа (p), остальная часть разрядной сетки n m предназначена для представления модуля мантиссы числа (m).

Нормализованное число - число в форме с плаваюей запятой, модуль мантисы m которого удовлетворяет следующему неравенству:

0.12 m <1.

 

Абсолютная погрешность представления - это разность между истинным значением входной величины А и ее значением, полученным из машинного изображения АМ, т.е. [A] = A - АМ

 

Относительная погрешность представления равна: [A] = [A]/АМ.

 

Систематический код - код, содержащий в себе, кроме информационных, также контрольные разряды, в которые записывается некоторая информация об исходном числе, необходимая для обнаружения возможных искажений в записи числа, возникших по тем или иным причинам. Например, код Хеминга является таким систематическим кодом.

 

Алгебра логики - это алгебра высказываний и она является логической основой компьютеров.

 

Высказывание - это всякое утверждение, которое может быть истинным или ложным. Истинному высказывани. приписывается символ 1, а ложному - 0. В алгебре логики цифры 0 и 1 явля.тся символами состояния или высказываниями, а не числами.