Синтез логических схем с одним выходом

 

Перед тем как перейти к примерам синтеза композиционных логических схем рассмотрим способы использования универсальности вентилей И-НЕ и ИЛИ-НЕ.

Свойство универсальности вентиля ИЛИ-НЕ:

 

Свойство универсальности вентиля И-НЕ:

 

Схемы с одним выходом и несколькими входами относятся к наиболее простым схемам. Основная сложность при синтезе этих схем состоит в том, чтобы найти выражение для выходной функции в заданном базисе.

Рассмотрим некоторые простые примеры перехода от логических уравнений к логическим цепям, т.е. примеры синтеза простых логических цепей. В частности, рассмотрим переход от представления функции в НДФ (ДНФ) к ее реализации на элементах И-НЕ и ИЛИ-НЕ.

Пусть задана функция 4-х переменных в НДФ:

F =CD +ABD + ABD +ABC + ACD.

Проведем ее минимизацию с помощью карты Карно:

 

AB = 00 AB = 01 AB = 11 AB = 10

CD = 00 1 1 1 1

CD = 01 1 1 1 1

CD = 11 0 0 0 0

CD = 10 1 0 1 0

 

Минимальная НДФ имеет вид: F = ABD + ABD + C.

Рассмотрим реализацию этого уравнения с помощью элементов И-НЕ. В общем случае на элементах И-НЕ НДФ функция реализуется посредством двух ступеней логики. На первой ступени получаются инверсные значения логических произведений и однобуквенных членов. На второй ступени выполняются операции И-НЕ, т.е. НЕ-ИЛИ, над полученными инверсиями.

Действительно, посредством применения двойного отрицания можно привести заданную функцию к виду:

 

F = ABD + ABD + C = ABD ABD C

 

Схема, соответствующая данному уравнению, приведена ниже.

 

В приведенной схеме для элементов первой и второй ступени применены различные, но эквивалентные условные обозначения. При реализации НДФ функции посредством элементов И-НЕ такой прием позволяет вести проектирование схем, пользуясь операциями И, ИЛИ и НЕ.

По рассмотреным ранее правилам из вышеприведенной карты Карно, может быть найдена минимальная НКФ заданной функции:

 

F = (C +D)(A +B +C)(A + B +C)\

 

Отсюда, взяв двойное отрицание и применив теорему Де Моргана, получим

 

 

F = [(CD)(ABC)(ABC)]

 

На элементах И-НЕ КНФ функции реализуется с помощью трех ступеней (соответствующая схема приведена ниже). На первой ступени посредством операции И-НЕ над инверсными значениями переменных, входящих в КНФ, образуются логические суммы. На второй ступени выполняется операция И-НЕ над логическими суммами и однобуквенными членами (если они имеются), тем самым образуется инверсное значение функции. На третьей ступени выполняется инверсия и получается искомая функция.

 

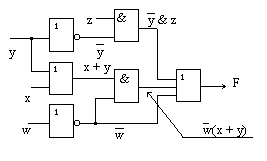
При минимизации логических функций для логических схем, которые предполагается строить на базе элементов И-НЕ или ИЛИ-НЕ, необходимо кроме собственно минимизации стремиться также к тому, чтобы структурная формула была представлена в виде комбинации из элементов И-НЕ или ИЛИ-НЕ. Тогда переход от структурной формулы к функциональной схеме не будет сложным. В любом случае при построении логической схемы в базисе И-НЕ на основе логической функции, представленной в МНДФ, необходимо везде вместо элементов И и ИЛИ ставить элемент И-НЕ. При построении логической схемы в базисе ИЛИ-НЕ на основе логической функции, представленной в МНКФ, необходимо везде вместо элементов И и ИЛИ ставить элемент ИЛИ-НЕ. Однако надо учесть, что есть точка зрения, по которой считается, что наиболее удобным для решения синтеза схем цифровых автоматов является базис И, ИЛИ, НЕ.

Рассмотрим, например, выражение F = w +y & z +w(x + y). Применив закон де Моргана, запишем его в следующем виде:

 

F = {w(yz) [w(x + y)]}

 

На основании последнего выражения реализуем эту функцию при помощи вентилей типа И-НЕ.

эта же функция, реализованная в базисе 1 будет иметь вид:

 

 

Как видим в этом случае схема реализовання в базисе 1 более компактна.

Теперь рассмотрим способы формирования схемы, реализующей функцию суммирования по модулю 2 (функция f6), в различных базисах. Логическая функция f6, как известно, в аналитическом виде представляется в виде:

F = AB +AB, и имеет следующую таблицу истинности:

A B F

0 0 0

0 1 1

1 0 1

1 1 0

 

В базисе И, ИЛИ, НЕ схема, реализующая функцию f6, имеет вид:

 

В базисе ИЛИ-НЕ:

 

 

F = AB + AB = A +B +A + B = A +B +A + B

 

В базисе И-НЕ:

 

F = AB + AB = AB AB

Более сложные схемы, имеющие несколько выходов, могут быть сведены в частном случае к набору схем с одним выходом. Тогда синтез осу-ществляется путем декомпозиции для каждой выделяемой схемы. Рас-смотрим для примера синтез одноразрядного двоичного сумматора методом декомпозиции, заданного таблично.

 

A B Ci S C0 AB = 00 AB = 01 AB = 11 AB = 10

0 0 0 0 0 Ci = 0 0 1 0 1

0 0 1 1 0 Ci = 1 1 0 1 0

0 1 0 1 0 S

0 1 1 0 1

1 0 0 1 0

1 0 1 0 1 AB = 00 AB = 01 AB = 11 AB = 10

1 1 0 0 1 Ci = 0 0 0 1 0

1 1 1 1 1 Ci = 1 0 1 1 1

C0

 

На выходе S имеется результат сложения двух одноразрядных чисел - A и B - и переноса Ci предыдущего сумматора; перенос, который при этом возникает, подается на выход C0. Ситезируемую схему можно рассматривать как схему, состоящую из двух частей: схемы для получения поразрядной суммы S (полусумматор) и схемы для получения переноса C0.

Из карт Карно видно, что возможно минимизировать только функцию C0. Для составления схемы сумматора могут быть использованы частично минимизированные функции и после различных алгебраических преоб-разований можно получить следующие дизъюнктивные нормальные формы для функций S и C0:

 

S =ABCi + ABCi +ABCi + ABCi = (A + B + Ci)C0 + ABCi

C0 = AB + CiA + CiB = AB + Ci(A + B)

 

На основании этих уравнений можно построить схему полного сумматора на элементах И, ИЛИ и НЕ.

Введем следующие обозначения: E = A B; D = AB; T = A + B.

Тогда:

S = E Ci; C0 = D + ECi; C0 =T + ECi.

 

Схему разряда полного двоичного сумматора построенного на элементах

И-НЕ в соответствии с последними уравнениями можно реализовать следующим образом:

Схему сумматора можно также сформировать при помощи двух полу-сумматоров:

 

Ci S

 

A

B C0

 

Для полусумматора справедливы следующие уравнения:

 

S =AB + AB; b C0 = AB или Pi = AB.

 

Полусумматоры могут быть реализованы в базисе И-НЕ следующим образом:

Полусумматор в базисе И, ИЛИ, НЕ несколько компактнее:

Но на практике обычно используют готовые полусумматоры, причем также как и готовые полные сумматоры, реализованные в виде интегральных схем.