
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение чисел, представленных в форме с плавающей запятойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При операции умножения чисел, представленных в форме с плавающей запятой их мантиссы умножаются, как числа с фиксированной запятой, а порядки складываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально складываются характеристики чисел, то умножение выполняется по следующей формуле:
A1 x A2 = m12
где r 1 + r 2 - l - характеристика результата. Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняются процедуры нормализации и округления ответа. Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие
0 r r max, где r max = l + p max. Рассмотрим пример: умножим числа с мантиссами m1 = 0,101 (5), m2 = 0,1 (2) и характеристиками r 1 = 1011, r 2 = 1010, l = 1000, p 1 = 3, p 2 = 2, p = p 1 + p 2 = 5, r = r 1 + r 2 - l = 001011 + 001010 - 001000 = 001101 = 1310 m = m1 x m2 = 0,01010, необходимо нормализовать ответ. Для этого в данном случае сдвигаем мантиссу влево на 1 разряд и вычитаем 1 из p, получаем p = 4. В итоге имеем m = 0,10102, p = 410 = 01002, r = 1210 = 11002.
Ускорение операции умножения
По времени выполнения операция умножения относится к длинным операциям. Затраты времени на умножение двух чисел в прямом коде можно оценить следующей формулой (для случая последовательного анализа разрядов множителя):
где t сдв - время выполнения сдвига числа на один разряд; t сл - время суммирования на сумматоре; p i - вероятность появления единицы в разрядах множителя; n - количество разрядов множителя. Существуют несколько методов ускорения процедуры умножения: анализ двух разрядов множителя одновременно, анализ произвольного количества разрядов множителя, умножение в системе счисления с основанием q =2kи матричные методы умножения. Рассмотрим первый спосо, ускорения умножения как наиболее наглядный и распространенный для целых чисел, представленных в прямом коде. В связи с тем, что в этом случае в процессе выполнения операции умножения на каждом цикле операции анализируется сразу два разряда множителя, то таких циклов понадобится n /2, где n - длина разрядной сетки множителя без учета знакового разряда. Это число циклов записывается в некоторый счетчик SС. При обнулении содержимого счетчика SС процедура умножения останавливается. Обычно анализируются два младших разряда множителя, поЭтому в конце каждого цикла производится одновременный сдвиг на два разряда вправо изображения суммы частных произведений (Р) и множителя. Причем, таким образом, чтобы при каждом таком сдвиге очередной младший разряд числа Р попадал в старший разряд мантиссы множителя. Обозначим эту процедуру условно как ПС. Очевидно, что в таком случае произведение будет сформировано в разрядной сетке первоначально отведенной для множителя. Если множимое X и множитель Y, а его два очередных младших разряда (y1y0), то в зависимости от результата анализа этих разрядов предусматриваются следующие действия. Если y1y0 = 00, то выполняются только процедуры: ПС и SС = SС-1. Если y1y0 = 01, то выполняются процедуры: Р = P + X, ПС и SС = SС-1. Если y1y0 = 10, то выполняются процедуры: сдвиг множимого влево на 1 разряд, т.е. умножение его на два, P = P + X, ПС и SС = SС-1. Если y1y0 = 11, то выполняются три раза P = P + X и ПС, SС = SС-1. Когда SС = 0 - операция умножения заканчивается. Как обычно перед началом самой процедуры умножения определяется знак произведения, проверяются на 0 X и Y, если кто-нибудь из них равен 0, то произведению сразу присваивается нулевое значение. Рассмотрим пример ускоренного умножения 310 на 7810, т.е. когда X = 3, а Y = 78. Если n = 10, то X = 0000000112, Y = 00010011102, а SС = 5.
512 256 128 64 32 16 8 4 2 1 X 00 00 00 00 11 множимое Y 00 01 00 11 10 множитель R 00 11 10 10 10 ответ = 234
В некотором регистре P будем формировать частные произведения. 1) Анализ 2-х младших разрядов Y. y1y0 = 10. Сдвинуть X на 1 разряд влево и прибавить к P.
P 00 00 00 00 00 +X 00 00 00 01 10 P 00 00 00 01 10 сдвиг на 2 разряда P и Y P 00 00 00 00 01 ---- 10 00 01 00 11 Y
2) y1y0 = 11, _ 3 раза прибавляем X к P P 00 00 00 00 01 +X 00 00 00 00 11 P 00 00 00 01 00 +X 00 00 00 00 11 P 00 00 00 01 11 +X 00 00 00 00 11 P 00 00 00 10 10 сдвиг на 2 разряда P и Y P 00 00 00 00 10 ---- 10 10 00 01 00 Y
3) y1y0 = 00, сдвиг на 2 разряда P и Y P 00 00 00 00 00 --- 10 10 10 00 01 Y
4) y1y0 = 01 P 00 00 00 00 00 +X 00 00 00 00 11 P 00 00 00 00 11 сдвиг на 2 разряда P и Y P 00 00 00 00 00 --- 11 10 10 10 00 Y
5) y1y0 = 00, сдвиг на 2 разряда P и Y P 00 00 00 00 00 --- 00 11 10 10 10 Y = 23410
Деление двоичных чисел
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 x m22
x m22  = (m1 x m2)2
= (m1 x m2)2 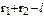 ,
, ,
,


