
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение на двузначное числоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При умножении на двузначное число до сознания школьников необходимо довести тот факт, что первый множитель умножается дважды: сначала на единицы множителя, а затем на десятки множителя. Это не сразу понимают все ученики, а поэтому и заканчивают умножение раньше, считая, что они все сделали, найдя первое промежуточное произведение. Многие учащиеся вспомогательной школы не осознают необходимости сложения двух промежуточных произведений.
Все это требует от учителя школы VIII вида тщательной неторопливого объяснения, а от учащихся — подробных расе у») дений, комментирования выполняемых действий. Рассуждения можно провести так: 246*32. Множитель — л! значное число. Оно состоит из 2 ед. и 3 дес. Сначала первь множитель 246 умножим на 2 ед. Затем 246 умножим на 3 дес или 30.
, 492 "*" 7380 К первому произведению прибавим второе. Мы произвели три действия: 1) умножили 246 на единицы множителя; 2) умножили 246 на десятки множителя; 3) сложили полученные произведения., ное число запись и вычисления производят так: множители заш сывают друг под другом, проводят черту и ставят знак умножени| слева. Умножают первый множитель на единицы второго и зат сывают полученное произведение под чертой. Это первое непо ное произведение. Умножение еще не закончено, первы] 246 множитель умножают на десятки второго и первс 32 число, полученное от умножения на десятки, записыв _1_ 492 ют П0д десятками (6 умножили на 3 десятка,
/ ОО ' Необходимо рассмотреть случаи умножения на двузначное •(ело, когда первый множитель оканчивается нулем (540x37). |т«6ы умножить 540 на 37, надо 54 десятка умножить на 37, Олучим 1998 десятков. К полученному произведению припишем уль, т. е. умножим его на 10. • Учитель может и не выделять как особые случаи умножение на |руглые десятки или умножение чисел, оканчивающихся нулями, |е изменяя при этом привычную для учащихся форму записи и |лгоритм вычисления, например: 540 х 37 3780 1620
От такой развернутой формы записи можно отказаться постепенно, подождав момента, когда учащиеся сами поймут, что при умножении на нуль неполное произведение всегда равно нулю и, его можно не записывать, Деление на двузначное число Деление на двузначное число впервые вводится в 7-м классе школы VIII вида. Первое знакомство с этим видом деления происходит на примерах внетабличного деления, а именно при делении двузначного числа на двузначное, когда в частном получается однозначное число. В этом случае частное отыскивается приемом округления делимого и делителя до круглых чисел. Например: «При отыскании частного 93:31 округляем делимое 93 до 90, делитель 31 до 30. Тогда 90:30=3. Значит, в частном надо взять по 3. Проверяем: 31x3=93. Ответ верен. Рассмотрим другой пример: 81:27. Округлим 81 до 80, а 27 до 30, получим 80:30. Можно взять по 2. Проверим: 27x2=54, 84—54=27. Значит, в частном должно быть большее число. Берем по 3. Проверяем: 27x3=81. Частное равно 3». Однако, как показывает опыт, такие рассуждения и множество промежуточных вычислений доступны не всем учащимся. Поэтому целесообразно учащихся познакомить с приемом деления, который доступен большинству умственно отсталых школьников, если они овладели приемом умножения двузначного числа на однозначное. Учитель показывает, что при делении на двузначное число труднее всего правильно подобрать цифру частного. Чтобы преодолеть эту трудность можно воспользоваться последовательным умноже- нием частного на числа 1, 2, 3 и т. д., пока не получится числ<> близкое к делимому. Например, 81:27. 27x1=27 — это число меньше 81. 27x2=54 — это число меньше 81. 27x3=81 — получилось число, равное делимому, значит, нал в частном взять по 3. Все промежуточные действия умножени для отыскания нужной цифры частного необходимо производить > тетради. Запись решения примера выглядит так:
27x1=27 ,27
х27 Х 3 ~8Т Далее последовательно рассматривается деление трех-, четы рех-, пяти- и шестизначных чисел на двузначное число. При решении всех этих примеров необходимо учитывать, что отделяемые две цифры делимого составляют число, которое либо равно, либо больше делителя, и только после этого рассматрива ются случаи, когда это число меньше делителя, и в этих случаях требуется отделить три цифры делимого.
23x1=23 23x2=46 35x1=35 35x2=70
,35
Х
5 Т75"
V73 Х 3 "2Т9" Наиболее успевающие по математике учащиеся постепенно сокращают число проб на умножение; умножение делителя на 1 они не записывают, некоторые устно умножают делитель на 2, а то я на 3, и начинают умножать на 4 и 5 и т. д. 240 Естественно, что сильным учащимся следует показать прием мкругления делимого и делителя. Например, рассматривается деление трехзначных чисел на дву-япачное число при однозначном частном и, например: 465:93. Рассуждения проводим так: «Делитель заменяем круглым числом.;->то число 90, или 9 десятков. В делимом тоже отделяем десятки, их 46. Делим 46 на 9. В частном берем 5. Проверяем, умножая <)3х5. В данном случае 5 подходит». Рассматриваются и случаи деления с остатком:
35 ТГост. 28)
Вслед за делением с остатком рассматривается деление трехзначного числа на двузначное, когда в частном получается двузначное число. Вначале в делимом подбираются такие числа, в которых первое неполное делимое состояло бы из двух цифр, а делитель состоял из цифр, не превышающих 5. «При выполнении деления делитель заменяем наименьшим круглым числом 20. В делимом отделяем две цифры. Первое неполное делимое — 80 десятков. В частном будет двузначное число. 80 делим на 20, будет по 4, но по четыре брать нельзя, так как 23x4=92. Берем по 3. Проверяем: 23x3=69, 80—69=11. Остаток меньше делителя. Значит, первую цифру подобрали правильно. 115 делим на 20. Берем первые две цифры делимого (11) и первую цифру делителя (2), 11 делим на 2. Берем по 5. Проверяем: 23x5=115. Вычитаем. Остатка нет. Значит, 5 подобрали правильно. Частное 35. Проверим умножением: 35x23=805». После этого рассматриваются случаи деления четырехзначного числа на двузначное. И наконец, рассматриваются такие случаи деления: число, состоящее из двух цифр делимого, не делится на делитель.
Рассуждения проводятся так: «17 тысяч не делятся на 43, тогда на 43 разделим 178 сотен. В частном получится трехзначное число — ставим 3 точки. Делитель 43 заменим меньшим круглым числом 40. Делим 178 на 40. Берем в делимом первые две цифры, а в делителе первую цифру. Получаем делимое 17, а делитель 4. 17 делим на 4. Берем по 4, проверяем умножением и т. д.». В методической литературе, связанной с вопросами начально обучения математике, после окончания деления ставится ну,) показывающий, что деление закончено и произведено без остап В школе VIII вида нуль записывать не рекомендуется. От показывает, что учащиеся (по аналогии с решением примеров, которых нули переносятся в частное из делимого) этот нуль си сят в частное, рассуждая при этом так: «О делим на 82, получа< ся нуль. В частное записываем нуль». Например:
Особое внимание необходимо уделять рассмс рению случаев, когда делимое оканчивается ну}. ми и когда нули получаются в середине частноГ] Подготовительными упражнениями являют! деление нуля (0:5, 0:12), а также решение пр! меров с небольшими числами вида 320:8=4| 312:3 и т. д. Рассмотрим решение пример 24 000:75. Рассуждения проводятся так:
«Первое неполное делимое — 240 сотен. Зн чит, в частном будет трехзначное число. Ставим точки. Округляем делитель до 70. Делим 240 I 70. Сначала 24 делим на 7. Берем по 3. Провер ем умножением. Остаток 15. Делим 150 дес. н«. 75. 15:7 берем по 2. Проверяем умножением. Десятки разделились все. Делим 0 единиц: 0:75=0. Пишем в частном 0. Частное 320». После изучения всех четырех арифметических действий для закрепления вычислительных навыков решаются примеры вида 626 640:84+212 760x36, (7368+28 300)х 12-17 899. Вопросы и задания 1.Составьте схему последовательности изучения нумерации многознач 2. Изготовьте эскизы таблиц для изучения нумерации многозначных 3. Сравните алгоритмы умножения (деления) многозначного числа на 4. Проанализируйте ошибки учащихся при выполнении четырех арифме Глава 14 МЕТОДИКА ИЗУЧЕНИЯ МЕТРИЧЕСКОЙ СИСТЕМЫ МЕР ОБУЧЕНИЕ ИЗМЕРЕНИЯМ В школе VIII вида учащиеся знакомятся с единицами измерения длины, стоимости, массы (веса), емкости, площади, объема и иремени, учатся производить измерения величин с помощью про-стейших инструментов. Занятия по данной теме способствуют формированию обобщений, совершенствованию целенаправленности и точности выполнения действий, воспитанию умения планировать деятельность, доводить любую работу до конца, формированию навыков самоконтроля. В ходе формирования практических умений и навыков развиваются внимание, память, наблюдательность, совершенствуются моторика, тактильные и зрительные ощущения. Все это служит решению задач коррекции как познавательной деятельности, так и личностных качеств школьников с нарушением интеллекта. В процессе знакомства с единицами измерения величин у учащихся расширяются представления о числе. Они убеждаются, что числа получаются не только от пересчета предметных совокупностей, но и в результате измерения величин. Изучение этого материала способствует лучшему пониманию закономерностей десятичной системы счисления (соотношение единиц измерения величин, кроме единиц измерения времени, основано на десятичной системе счисления), расширению понятий арифметических действий (арифметические действия можно производить и над числами, записанными с употреблением единиц измерения величин, законы арифметических действий над числами, полученными от пересчета предметных совокупностей, остаются справедливыми и для чисел, полученных от измерения). Производя действия над числами, учащиеся закрепляют навыки предварительного анализа задания, вычленяют черты сходства и различия в действиях с различными (по виду) числами. Изучение данной темы позволяет тесно связать преподавание математики с жизнью: учащиеся получают практические умения и навыки измерения, необходимые как в повседневной жизни, так и при овладении будущими профессиями, учатся правильно пользоваться измерительными инструментами — линейкой и рулеткой (устанавливать линейку, вести отсчет единиц измерения от нуле- вого деления линейки, а также от любого другого деления), веса ми (уравновешивать весы, производить взвешивание на чашечны/ весах, циферблатных весах со стрелкой), часами (определят! время по часам с точностью до минуты) и т. д. Данная тема, несмотря на большую по сравнению с другими разделами математики конкретность, трудна для учащихся вспомога тельной школы. У учащихся как младших, так и старших классов нет реальных представлений о единицах измерения величины, на блюдается смешение единиц измерения одной и той же величины (сантиметра с дециметром и метром) и разных систем мер (метра с квадратным метром, а иногда и с килограммом). Учащиеся путают единицы измерения и измерительные инструменты. Плохое знание единиц измерения величин и неумение различать их создают большие трудности при установлении соотношения мер. При изучении данной темы учащиеся допускают самые разнообразные ошибки. Например, при выполнении действий с числами, полученными от измерения, наименования не принимаются во внимание (5 м+6 см=65), в записи этих чисел переставляются местами единицы мер (4 м 40 км), часто при выполнении действий записываются случайные наименования (125x80=10 бОО кв. м=1000 р.). Главной причиной этих ошибок является отсутствие конкретных представлений о размерах каждой единицы измерения. Для школьников с нарушением интеллекта также характерна неточность измерений. Это вызвано непониманием значения точности измерения в практике, неумением правильно установить инструмент, выбрать соответствующую единицу измерения, произвести отсчет по шкале измерительного инструмента (линейки, весов, циферблатов часов), правильно записать результат измерения. Для преодоления указанных трудностей необходимо руководствоваться следующими требованиями: 1.В младших классах надо стараться сформировать представле 2. Знакомство с новой единицей измерения целесообразно на 3. Нужно стремиться (учитывая слабость воображения, малый практический опыт, конкретность мышления умственно отсталых), чтобы учащиеся ощутили, четко представили каждую единицу измерения, используя все органы чувств. Надо шире использовать Наблюдения, опыт, знание уж известных единиц измерения. Например, при знакомстве с мерой длины 1 км использовать знание 1 м, пройти с учащимися расстояние 1 км и отметить; затраченное время. , Меры, которые трудно или невозможно ощутить (например, массу грузов в 1 ц или в 1 т), надо показать опосредованно, Приводя примеры использования этих мер. , 4. Изучение мер должно сопровождаться активной практической деятельностью самих учащихся: а) по изготовлению единиц измерения (метра, дециметра, сантиметра, миллиметра, квадратных и кубических мер); б) по измерению величин с помощью инструментов; в) по выяснению соотношения мер (в дециметре укладывать сантиметры, метр делить на дециметры и сантиметры, приходя к выводу: 1 дм = 10 см, 1 м=10 дм=100 см). При изучении данной темы учащиеся должны получить представление о размерах некоторых наиболее часто встречающихся в их опыте и опыте других людей предметов, знание которых поможет им лучше ориентироваться в окружающей жизни, подготовит к участию в доступной им трудовой деятельности. Например, учащиеся должны знать средний рост ребенка их возраста, средний рост взрослого человека, длину и ширину тетради, классной доски, высоту, длину и ширину класса, длину карандаша, среднюю длину шага, высоту стола, стула, массу одного яблока, картофелины, буханки хлеба, батона, мешка картофеля (зерна, муки), среднюю массу человека, грузоподъемность машины, вместимость ведра, молочных бидонов, среднюю скорость пешехода, лошади, автомашины, поезда, самолета, уметь показать примерные размеры 1 см и 1 м. 5. Изучение мер должно сопровождаться развитием глазомера и мускульных ощущений. Кроме того, учащиеся должны приобрести умение оценивать приближенные результаты измерений (если остаток меньше половины единицы измерения, то он отбрасывается; если остаток равен или больше половины единицы измерения, то к полученным целым единицам мер добавляется еще одна единица, например: 1 м 30 см«1 м, 1 м 50 см«2 м, 1 м 80 см=2 м). 6. Закрепление знаний мер и умения измерять проводится 7. Измерению с помощью инструментов для определения точн| 8. Формирование навыков у детей с нарушением интеллект Весьма полезной для закрепления знаний о единицах измерения, для выработки практических навыков по измерению и использованию измерительных инструментов, для установления связи знаний с жизнью является дидактическая игра «Магазин». Эту игру нужно проводить систематически с 1-го по 4-й класс. Наряду с игрой «Магазин» необходимо организовывать игры «Почта», «Поездка на транспорте» и др.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.01 с.) |

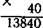

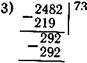 73x1=73
73x1=73


