
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обусловленность задачи вычисления корня
Будем предполагать, что в достаточно малой окрестности корня
где Для Этот интервал называется интервалом неопределенности корня Найдем оценку величины ε. Пусть
Тогда неравенство (4.24) примет вид:
Отсюда
Следовательно:
где
4.3. Порядок выполнения работы 1. Изучить раздел 4.2 настоящих методических указаний. 2. Проверить условие сходимости и записать расчетные формулы для нахождения корня уравнения заданными методами. Варианты индивидуальных заданий представлены в таблице вариантов (Приложение В4, таблица B4.1). 3. Выбрать и обосновать выбор начального приближения из указанного отрезка поиска корня. 4. Написать и отладить программы решения нелинейного уравнения с точностью 5. Сравнить полученное значение корня с истинным значением корня, приведенным в таблице вариантов. 6. Сделать анализ полученных результатов и составить отчет о проделанной работе. Содержание отчета о выполнении работы 1. Цель работы. 2. Постановка задачи. 3. Краткое описание рассматриваемых методов решения нелинейных уравнений. 4. Анализ сходимости предлагаемых методов для решения поставленной задачи. 5. Обоснование выбора начального приближения из указанного отрезка поиска корня. 6. Результаты вычислительного эксперимента. 7. Анализ полученных результатов и выводы об их соответствии теоретически ожидаемым. 8. Приложения. 4.5. Контрольные вопросы 1. Сформулируйте постановку задачи поиска корня нелинейного алгебраического уравнения.
2. Каковы основные этапы поиска корня нелинейного алгебраического уравнения? 3. Дайте определение понятию «простой корень». 4. Что собой представляет корень кратности k? 5. Какие основные методы решения задачи поиска корня нелинейного алгебраического уравнения Вы знаете? 6. В чём состоит суть модификации классического метода Ньютона-Рафсона для решения нелинейных алгебраических уравнений? 7. Дайте определение понятию «сходимость» при решении задачи поиска простых корней. 8. Какие методы поиска корней нелинейных уравнений называются многошаговыми? Приведите примеры одношаговых и многошаговых методов. 9. Что такое «интервал неопределенности» при поиске корня? 10. Как определить радиус интервала неопределённости при решении задачи поиска простого корня нелинейного уравнения с заданной точностью?
5. Лабораторная работа №5 «Численное решение дифференциальных уравнений»
5.1. Цель работы Получить навыки применения методов численного решения дифференциальных уравнений. 5.2. Краткие теоретические сведения Обыкновенным дифференциальным уравнением (ОДУ) называется выражение:
где х - независимая переменная; y(х) - искомая функция (решение дифференциального уравнения);
Порядок старшей производной, входящей в уравнение (5.1) называется порядком дифференциального уравнения. Функция Каждое дифференциальное уравнение имеет в общем случае бесконечное множество решений. Для нахождения частного решения необходимо указать начальные условия, а именно: задать значения
Уравнение (5.1) называется разрешенным относительно старшей производной, если оно имеет вид:
Задача отыскания решения уравнения (5.3) при начальных условиях (5.2) называется задачей Коши для обыкновенного дифференциального уравнения. Уравнение (5.3) сводится к системе n обыкновенных дифференциальных уравнений первого порядка заменой на независимую функцию: y¢ на P1(x); y¢¢ - на P2(x); …, y(n-1) - на P(n-1)(x).
Таким образом, имеем:
причем Часто решение уравнения не удается найти в общем виде. Поэтому возникает необходимость применять те или иные методы, дающие приближенное решение задачи: Метод степенных рядов.
Решение находится в виде сумм ряда:
Приближенное решение задачи дает частичная сумма этого ряда;
2) метод Эйлера для уравнения
В процессе решения составляется таблица значений где Значения yk+1 определяются по формуле:
Погрешность вычислений на каждом шаге составляет
где
|
||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.165.246 (0.011 с.) |
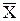 выполняется неравенство:
выполняется неравенство: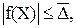 (4.24)
(4.24) – предельное значение абсолютной погрешности вычисления функции. Если функция f непрерывна, то найдется такая малая окрестность
– предельное значение абсолютной погрешности вычисления функции. Если функция f непрерывна, то найдется такая малая окрестность  корня
корня  знак вычисленного значения f*(Х) в общем случае не обязан совпадать со знаком функции f(Х) и, следовательно, становится невозможно определить, какое именно значение Х из интервала
знак вычисленного значения f*(Х) в общем случае не обязан совпадать со знаком функции f(Х) и, следовательно, становится невозможно определить, какое именно значение Х из интервала  (4.25)
(4.25) (4.26)
(4.26) . (4.27)
. (4.27) (4.28)
(4.28)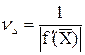 - абсолютное число обусловленности задачи вычисления коней нелинейного алгебраического уравнения..
- абсолютное число обусловленности задачи вычисления коней нелинейного алгебраического уравнения.. . В программе предусмотреть подсчет и вывод числа итераций, за которое удается найти значение корня с заданной точностью.
. В программе предусмотреть подсчет и вывод числа итераций, за которое удается найти значение корня с заданной точностью.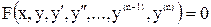 (5.1)
(5.1) - производные порядка 1, 2,..., n функции y(х).
- производные порядка 1, 2,..., n функции y(х). называется решением уравнения (5.1), если при подстановке ее в выражение (5.1) последнее обращается в тождество.
называется решением уравнения (5.1), если при подстановке ее в выражение (5.1) последнее обращается в тождество. при
при  , т.е.
, т.е.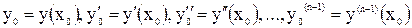 . (5.2)
. (5.2) (5.3)
(5.3) (5.4)
(5.4) .
. (5.5)
(5.5)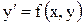 с начальным условием
с начальным условием  .
. ,
, - отрезок, на котором ищется решение.
- отрезок, на котором ищется решение. . (5.6)
. (5.6) , (5.7)
, (5.7) ;
;


