
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №4 «Численное решение нелинейных уравнений»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К лабораторным занятиям по дисциплине «Информатика и системология» для студентов направления подготовки «Экология» дневной формы обучения
Севастополь УДК 519.61
Методические указания к лабораторным занятиям по дисциплине «Информатика и системология» для студентов направления подготовки «Экология» дневной формы обучения / Сост. Е.В. Козлова. – Севастополь: Изд-во СевНТУ, 2011.– 48с. Цель методических указаний – методическая помощь в самостоятельном изучении дисциплины и выполнении лабораторных работ.
Методические указания рассмотрены и утверждены на заседании кафедры кибернетики и вычислительной техники (протокол № от 2011г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензент: Обжерин Ю.Е., доктор технических наук, зав. кафедрой высшей математики.
Ответственный за выпуск: Скатков А.В., доктор технических наук, профессор, зав. кафедрой кибернетики и вычислительной техники.
СОДЕРЖАНИЕ
Введение
Целью лабораторного практикума по дисциплине «Информатика и системология» является освоение студентами основ вычислительных методов, применяемых для решения инженерных задач, овладение навыками реализации вычислительных алгоритмов на ЭВМ и оценки достоверности полученных результатов. В настоящих методических указаниях представлены основные теоретические положения по следующим разделам: - «Исследование погрешностей результатов вычислений при решении задач вычислительной математики», - «Приближение функций», - «Численное дифференцирование и интегрирование функций», - «Численное решение дифференциальных уравнений», а также варианты заданий к выполнению соответствующих лабораторных работ. Каждый раздел построен по стандартной схеме, включающей формулировку цели выполнения лабораторной работы, описание базовых теоретических сведений, примеры решения типовых задач, ссылки на варианты индивидуальных заданий и список контрольных вопросов. Номер варианта индивидуального задания для выполнения лабораторной работы выбирается как остаток от деления по модулю номера в списке группы на максимальный номер варианта в таблице вариантов заданий для соответствующей лабораторной работы. По результатам выполненной работы оформляется отчет, включающий в себя следующие разделы: - цель работы; - постановка задачи; - обоснование выбора метода решения поставленной задачи; - вычислительные алгоритмы; - тексты программ (программы могут быть написаны на любом языке программирования в любой операционной среде, не возбраняется использование любых пакетов прикладных программ и специализированных сред);
- основные результаты решения поставленной задачи; - выводы о проделанной работе. При выполнении домашних заданий и подготовке к выполнению лабораторных работ рекомендуется использовать учебную и справочную литературу [1-9]. В приложении А приведен пример оформления титульного листа отчёта о выполнении лабораторной работы. В приложение В содержит варианты индивидуальных заданий для выполнения лабораторных работ. Отчёт о выполнении работы должен быть выполнен аккуратно, содержать все необходимые пояснения и промежуточные результаты. В разделе «Выводы» должен быть проведён анализ полученных результатов и сформулированы соответствующие рекомендации, если это следует из постановки задачи. 1. Лабораторная работа №1 «Исследование погрешностей результата вычислений при решении задач вычислительной математики» 1.1. Цель работы Овладение студентами навыками вычисления предельных абсолютной и относительной погрешностей результата вычислений и применения правил округления приближенных чисел в узком и широком смысле. 1.2. Основные понятия элементарной теории погрешностей Теория погрешностей вычислений - раздел вычислительной математики, изучающий причины возникновения и способы оценки всевозможных погрешностей решения задач на ЭВМ. Мерой точности вычислений могут служить либо предельные абсолютные погрешности
либо предельная относительная погрешность:
Формулы точного подсчета погрешностей имеют вид:
где m - рациональное число. Здесь Δ - абсолютная погрешность приближенного числа; Абсолютные и относительные погрешности для приближенных вещественных чисел тесно связаны с важным понятием верных значащих цифр. Если абсолютная погрешность числа x (Δх) не превышает половины единицы разряда последней цифры в записи числа x, то говорят, что у числа x все знаки верны. Приближенные числа следует записывать, сохраняя их и отмечая только верные знаки. При подсчете значащих цифр не считаются нули слева. Например, 0,00139 имеет три верных значащих цифры. Если число х в десятичном представлении имеет, по крайней мере, t верных значащих цифр, то его относительная погрешность Δх £10-t. Если десятичное число х имеет не более р верных значащих цифр, то его относительная погрешность Δх >10-p. Наоборот, у числа х с относительной погрешностью Δх³ Δ+х верны не более р значащих цифр, где р - наибольшее целое, удовлетворяющее неравенству Δ+х £10-p+1. Если х имеет относительную погрешность Δ(х)£Δ-(х), то х имеет не менее q десятичных значащих цифр, где q - наибольшее целое число, удовлетворяющее неравенству Δ-(х)<10-q. Таким образом, если имеется множество чисел xk,
1.3. Образцы выполнения заданий Задание 1. 1.1. Определить, какое равенство точнее: 1.2. Округлить сомнительные числа, оставив верные знаки: а) б) 1.3. Найти предельные абсолютные и относительные погрешности, если они имеют только верные цифры:
а) 0,4357 в узком смысле; б) 12,348 в широком смысле.
Решение задачи 1.1. Находим значения данных выражений с большим числом десятичных знаков:
Затем вычисляем предельные абсолютные погрешности, округляя их с избытком: Δх1=|0,81818-0,818|£0,00019, Δх2=|4,2426-4,24|£0,0027. Предельные относительные погрешности составляют: Δ1 Δ2 Так как Δ1 <Δ2, то равенство
Решение задачи 1.2 (а). Пусть По правилам округления найдем приближенное значение числа х, сохранив десятые доли и обозначим его:
Полученная погрешность больше 0,073>0,05, значит нужно уменьшить число цифр в записи приближенного числа до двух:
Так как
Решение задачи 1.2(б). Пусть В данном числе верными в широком смысле являются три цифры (2,3 и 5), поскольку Поэтому округляем его, сохраняя эти три цифры:
Это означает, что в округленном виде число 2,35 имеет все верные в широком смысле цифры. Решение задачи 1.3. (а) Так как известно, что все четыре цифры числа х=0,4357 верны в узком смысле, то абсолютная погрешность этого числа не превышает половины значащего разряда, стоящего на пятом месте после запятой, т.е. (б) Так как все пять цифр числа х=12,348 верны в широком смысле, то его погрешность не превышает единицы последнего (в нашем случае третьего) значащего разряда после запятой, т.е. Задание 2. 2.1. Вычислить значение выражения и определить погрешности результата.
2.2. Вычислить значение выражения, пользуясь правилами подсчета цифр.
Решение задачи 2.1. Вычислим значение исследуемого выражения:
Далее получим относительные погрешности операндов, входящих в выражение:
и запишем погрешность, получаемую при вычислении величины х:
Результат наших вычислений выглядит так:
Решение задачи 2.2. Имеем:
Решение задачи 2.3. Если операнды в вычисляемом выражении заданы без указания погрешностей, то предполагается, что все цифры в записи каждого операнда – верные. В этом случае при вычислении значения заданного выражения используется правило подсчёта цифр, которое гласит: «Если в операцию вступают операнды с одинаковым числом значащих цифр, то результат выполнения этой операции имеет такое же число значащих цифр. Если же в операцию вступают операнды с различным числом значащих цифр, то результат выполнения этой операции по точности совпадает с менее точным операндом».
Порядок вычисления выражения определяется приоритетами соответствующих операций. Округления производятся последовательно на каждом этапе вычислений. Сначала находим результат вычисления выражения в скобках:
Затем продолжим вычисления с учётом поэтапно получаемых результатов: h2= (11,8)2=139,2; M=(3,142×139,2) 19,8=437,4×19,8=8660,5.
1.4. Порядок выполнения работы 1. Изучить разделы 1.2, 1.3 настоящих указаний. 2. Для варианта, выбранного из таблиц B1.1 и B.2 (Приложение В), выполнить задания 1 и 2. 3. Составить отчет о выполнении работы. 1.5. Контрольные вопросы 1. Что такое погрешность? 2. Каковы основные источники возникновения погрешностей? 3. Дайте определения абсолютной и относительной погрешности. 4. Что такое верная и значащая цифра в записи приближенного числа? Всегда ли верная цифра в числе совпадает со значащей цифрой? 5. Дайте определение верной цифры в широком (узком) смысле слова. 6. Как учитываются погрешности исходных данных при вычислении арифметических выражений? 7. Каковы основные правила округления результата вычислений, если погрешности операндов явно не заданы? 2. Лабораторная работа №2 «Приближение функций» 2.1. Цель работы
Целью данной лабораторной работы является изучение и практическое применение методов приближения функций.
2.2. Основные теоретические положения и расчетные формулы
Задача интерполирования функций состоит в приближенной замене функции f(x) более простой интерполирующей функцией F(x), значения которой в узлах интерполирования xj (j=1, 2, …n) совпадают с соответствующими значениями f(x), т.е. справедливо равенство f(xj)=F(xj). (2.1) На практике чаще всего интерполируют функции f(x), заданные таблично, в точках xj (j=1, 2, …n), если необходимо узнать f(x) при x≠xj. Обычно F(x) отыскивают в виде обобщенного многочлена
где а ci - действительные коэффициенты, определяемые из линейной алгебраической системы:
Пусть Тогда ci определяется единственным образом и F(x) совпадает с интерполяционным многочленом Лагранжа:
При вычислении коэффициентов Лагранжа разности удобно расположить следующим образом:
Если обозначить произведение элементов соответствующих строк через
В случае равноотстоящих узлов интерполяционная формула Лагранжа имеет вид:
Для оценки погрешности интерполяционной формулы Лагранжа можно использовать следующее соотношение:
где [a,b] - интервал интерполирования. Существенным недостатком интерполяции по Лагранжу является тот факт, что при известном значении многочлена Pn(x), построенного по значениям yi (i=1, 2, …, n) в точках xi - введение нового (n+1)-го узла требует проведения всех вычислений заново.
Этим недостатком не обладает многочлен интерполирования Ньютона. Интерполяционная формула Ньютона (2.8)для неравноотстоящих значений аргумента:
где Отношение Отношение Разделенные разности m-го порядка имеют вид:
Для равноотстоящих узлов разделенные разности m-того порядка вычисляются по формуле:
где В точке x≠xi погрешность интерполяции: f(x) -Pn(x)≈ A(x0, x1, …, xn)×(x-x0)×(x-x1)×…(x-xn). Pn+1(x) – Pn(x)= A(x0, x1,…,xn+1)×ωn+1(x), где ωn+1(x)=(x-x0)×(x-x1)×…(x-xn). Если функция f(x) достаточно гладкая и величина |xn+1–xn| мала, то справедливо: A(x0, x1, …, xn) ≈A(x0, x1, …, xn+1) и тогда: f(x) -Pn(x) ≈ Pn+1(x) -Pn(x) и Δинт многочлена Ньютона=| Pn+1(x) – Pn(x) |. (2.11)
2.3. Порядок выполнения работы 1. Изучить раздел 2.2 настоящих методических указаний. 2. Для варианта, выбранного из таблиц B2.1 и B.2 (Приложение В), выполнить задания 1 и 2. 3.Рассчитать погрешности интерполяции для всех рассматриваемых случаев. 4. Сделать анализ полученных результатов и обосновать полученные решения, дать рекомендации по использованию рассмотренных методов. 3. Составить отчет о выполнении работы.
Содержание отчета о выполнении работы 1. Цель работы. 2. Постановка задачи. 3. Краткое описание рассматриваемых методов приближения функций. 4. Результаты вычислительного эксперимента. 5. Анализ полученных результатов и выводы об их соответствии теоретически ожидаемым. 6. Приложения. 2.5. Контрольные вопросы 1. Сформулируйте постановку задачи приближения функций. Приведите примеры практического применения решения подобных задач. 2. Что собой представляет задача интерполяции и чем она отличается от задачи аппроксимации? 3. Приведите геометрическую интерпретацию этих задач 4. Какие методы интерполяции Вы знаете? 5. Перечислите достоинства и недостатки известных Вам методов. 6. Как оценить точность решения задачи интерполяции различными методами? 7. Зависит ли точность полученных результатов интерполяции от равномерности размещения узлов интерполяции по числовой оси? Если да, то почему? 8. Что собой представляет задача экстраполяции функции? Чем она отличается от задачи интерполяции? 3. Лабораторная работа №3 «Численное дифференцирование и интегрирование» 3.1. Цель работы Целью данной лабораторной работы является овладение студентами практическими навыками применения методов численного дифференцирования и интегрирования функций, заданных табличным способом, а также навыков проведения оценок полученных результатов относительно погрешностей и коэффициентов обусловленности. 3.2. Основные теоретические положения и расчетные формулы Численное дифференцирование применяется тогда, когда функцию трудно или невозможно продифференцировать аналитически. Например, необходимость в численном решении задачи дифференцирования возникает в том случае, когда функция задана таблицей. Кроме того, формулы численного дифференцирования широко используются при разработке вычислительных методов решения многих задач: решения дифференциальных уравнений, поиска решений нелинейных уравнений, поиска экстремума функций и др. Основные формулы численного дифференцирования:
1. Основанные на первой интерполяционной формуле Ньютона (3.1):
2. Основанные на первой формуле Гаусса:
2. Основанные на второй формуле Гаусса:
3. Основанные на формуле Стирлинга:
4. Основанные на формуле Бесселя:
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым изменениям погрешностей исходных данных. Задачу называют хорошо обусловленной, если малым погрешностям исходных данных отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения. Мера степени обусловленности вычислительной задачи – число обусловленности. Эту величину можно интерпретировать как коэффициент возможного возрастания погрешностей в решении по отношению к вызвавшим их погрешностям входных данных. Пусть между абсолютными погрешностями исходных данных X и решения Y установлено неравенство: D(Y*)£JD ×D(X*). (3.6) Тогда величина JD называется абсолютным числом обусловленности. Если же установлено неравенство: d(Y*)£Jd ×d(X*), (3.7) то величину Jd называют относительным числом обусловленности. Для плохо обусловленной задачи J>>1. Несмотря на внешнюю простоту формул численного дифференцирования, их применение требует особой осторожности. Используемые при численном дифференцировании приближенные значения f*(X) функции f(X) непременно содержат ошибки измерения или вычисления. Поэтому к погрешности аппроксимации формул численного дифференцирования добавляется неустранимая погрешность, вызванная погрешностями вычисления функции f. Для того чтобы погрешность аппроксимации была достаточно малой, требуется использование таблиц с малым шагом h. Однако при малых значениях шага h формулы численного дифференцирования становятся плохо обусловленными. Поясним это на примере. Полная погрешность для простейшей формулы численного дифференцирования равна:
и представляет собой сумму погрешности аппроксимации
и неустранимой погрешности
Если`D - верхняя граница абсолютной погрешности D(f*(X))=|f(X) – f*(X)|, при вычислении функции f(X). Тогда неустранимая погрешность оценивается как
Эта оценка означает, что абсолютное число обусловленности JD=2/h, и так как JD®¥ при h ®0, исследуемая формула численного дифференцирования при малых значениях h становится плохо обусловленной. Формулы для вычисления производных порядка k>1 обладают еще большей чувствительностью к ошибкам задания функций. Основные формулы численного интегрирования: а) Пусть отрезок интегрирования [a,b] разбит на n частей с шагом Тогда простейшие формулы численного интегрирования имеют вид: -формула левых прямоугольников
-формула правых прямоугольников
-формула средних прямоугольников
где
Остаточные члены этих формул соответственно равны
где
б) формула трапеций:
где причем
в) формула Симпсона (число узлов n обязательно четное):
причем
г) формула Ньютона-Котеса для многочлена степени k:
где Коэффициенты Bk, ai(k) и остаточные члены rk(h) определяют заранее и для них составлена таблица 3.1:
Таблица 3.1 Параметры некоторых частных формул Ньютона-Котеса
д) формула Гаусса:
где Значения
Таблица 3.2 Узлов и весов квадратурной формулы Гаусса
3.3. Примеры решения типовых задач Задача 3.1. Определить абсолютное число обусловленности для следующей формулы численного дифференцирования:
Значения дифференцируемой функции y(x) заданы с предельной абсолютной погрешностью ε=10-3 и h=0,05.
Решение задачи 3.1. В соответствии с правилом учета абсолютных погрешностей при выполнении алгебраического суммирования можно утверждать, что абсолютная погрешность при вычислении конечной разности первого порядка Δy0 не превышает 2ε. Так как конечная разность второго порядка в узле х0 вычисляется как Δ2y0=Δy1-Δy0, то её абсолютная погрешность не превышает величины 2(2ε)=4ε. Аналогично, абсолютная погрешность при вычислении конечной разности третьего порядка не превышает величины 2(2 (2×ε))=8ε. Таким образом, погрешность вычисления первой производной по предложенной формуле удовлетворяет неравенству:
то есть Коэффициент, связывающий погрешность результата вычисления первой производной Задача 3.2. В условиях задачи 3.1. определить, каким должен быть оптимальный шаг дифференцирования, и является ли заданный шаг изменения аргумента (h=0,05) таблицы значений дифференцируемой функции близким к оптимальному. Решение задачи 3.2. Оценка максимальной погрешности интерполяции исходной функции на всем отрезке дифференцирования [a, b] для четырёх узлов интерполяции (n=3) удовлетворяет условию:
где Полная погрешность для формулы (3.14) представляет собой сумму вычислительной и погрешности интерполяции на интервале дифференцирования и не превосходит величины:
Минимизация по h функции ε1(h) приводит к следующей формуле для вычисления оптимального значения шага дифференцирования:
Вычислив максимальное значение производной четвёртого порядка (используя простейшие формулы численного дифференцирования) для заданного представления исходной функции, можно легко получить значение оптимального шага численного дифференцирования для заданной постановки задачи. 3.4. Порядок выполнения лабораторной работы
1. Изучить раздел 3.2 настоящих методических указаний. 2. Получить решение задачи численного дифференцирования. 2.1. В соответствии с вариантом индивидуального задания (Приложение В3, таблица B3.1) написать и отладить программы численного дифференцирования таблично заданной функции. 2.2. Для заданных формул численного дифференцирования вычислить коэффициенты обусловленности, сравнить полученные значения и сделать соответствующие рекомендации по применению соответствующих методов. 2.3. Определить оптимальное значение шага численного дифференцирования для достижения заданного значения точности решения. Сравнить полученное значение оптимального шага с заданным шагом аргумента в табличном представлении функции и сделать соответствующие рекомендации по изменению процедуры проведении последующих измерений значений функции. 3. Получить решение задачи численного интегрирования. 3.1. В соответствии с вариантом индивидуального задания (Приложение В3, таблица B3.2) написать и отладить программы численного интегрирования таблично заданной функции. 3.2. Оценить точность полученного решения. 4. Составить отчет о выполнении лабораторной работы.
Содержание отчета о выполнении работы 1. Цель работы. 2. Постановка задачи. 3. Краткое описание рассматриваемых методов численного дифференцирования и интегрирования функций. 4. Анализ обусловленности задач численного дифференцирования и интегрирования. 5. Определение оптимального шага для решения задач численного дифференцирования предложенными методами 6. Результаты вычислительного эксперимента. 7. Анализ полученных экспериментальных результатов и выводы об их соответствии теоретически ожидаемым. 8. Приложения. 3.6. Контрольные вопросы 1. Сформулируйте постановку задачи численного дифференцирования. 2. Какие простейшие формулы численного дифференцирования Вы знаете? 3. Дайте определение понятию «хорошо обусловленная задача». Является ли задача численного дифференцирования хорошо обусловленной? 4. Как вычислить абсолютное число обусловленности для заданного метода численного дифференцирования? 5. Как выбрать оптимальный шаг численного дифференцирования? 6. Сформулируйте постановку задачи численного интегрирования. 7. Является ли задача численного интегрирования хорошо обусловленной? 8. Какие простейшие формулы численного интегрирования Вы знаете? 9. Какая основная идея положена в основу метода Гаусса для численного интегрирования? 10. Как оценить точность простейших методов численного интегрирования? Метод Ньютона – Рафсона
Модификации метода Ньютона
Основным недостатком метода Ньютона является необходимость вычисления значения производной f¢(X) на каждой итерации. Рассмотрим некоторые модификации, лишенные этого недостатка. Заметим, что рассматриваемые ниже итерационные методы решения нелинейного уравнения на каждой итерации используют процедуру его линеаризации, то есть исходное нелинейной уравнение заменяется приближенно более простым линейным уравнением. -Упрощенный метод Ньютона Если производная функции f¢(X) непрерывна, то ее значение вблизи простого корня |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.130.38 (0.019 с.) |

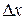 , представляющие собой разность между истинным значением величины х и ее приближенным значением
, представляющие собой разность между истинным значением величины х и ее приближенным значением 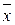 :
: (1.1)
(1.1)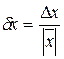 (1.2)
(1.2)
 - относительная погрешность приближенного числа.
- относительная погрешность приближенного числа. с относительной погрешностью Δ(х)max к максимальному значению
с относительной погрешностью Δ(х)max к максимальному значению 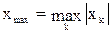 , то все числа группы могут быть записаны с помощью не более чем r+1 десятичных разрядов, где r - наибольшее целое число, для которого 10-r ³ Δ(х)max.
, то все числа группы могут быть записаны с помощью не более чем r+1 десятичных разрядов, где r - наибольшее целое число, для которого 10-r ³ Δ(х)max. .
. в узком смысле;
в узком смысле; в широком смысле.
в широком смысле.


 является более точным.
является более точным. . Согласно условию, погрешность
. Согласно условию, погрешность  ; это означает, что в числе 72,353 верными в узком смысле являются цифры, стоящие на следующих местах относительно десятичной запятой: **.*, то есть цифры 7,2, и 3.
; это означает, что в числе 72,353 верными в узком смысле являются цифры, стоящие на следующих местах относительно десятичной запятой: **.*, то есть цифры 7,2, и 3.

 , то обе оставшиеся цифры верны в узком смысле.
, то обе оставшиеся цифры верны в узком смысле. тогда
тогда 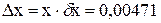 .
. .
. .
. а относительная погрешность
а относительная погрешность  .
.


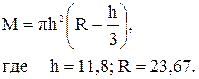

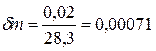 ,
,

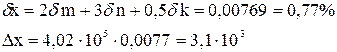

 Результат:
Результат:  .
.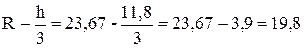 .
. , (2.2)
, (2.2) - линейно-независимая система функций,
- линейно-независимая система функций, (2.3)
(2.3) .
.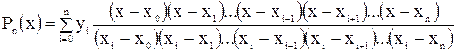 (2.4)
(2.4) , а произведение элементов главной диагонали - через
, а произведение элементов главной диагонали - через  , то формула (2.4) будет иметь вид:
, то формула (2.4) будет иметь вид: (2.5)
(2.5) (2.6)
(2.6)
 .
. , (2.7)
, (2.7)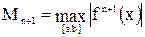 ,
,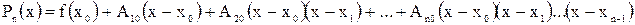 ,
,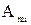 - разделенные разности m-того порядка.
- разделенные разности m-того порядка. называются разделенными разностями 1-го порядка.
называются разделенными разностями 1-го порядка. - разделенными разностями 2-го порядка.
- разделенными разностями 2-го порядка. (2.9)
(2.9) (2.10)
(2.10) - шаг интерполирования,
- шаг интерполирования,  .
.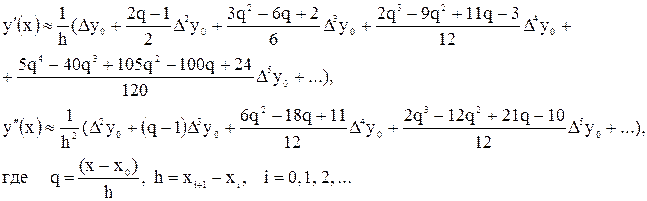
 - конечная разность i-го порядка, причем
- конечная разность i-го порядка, причем
 (3.2)
(3.2)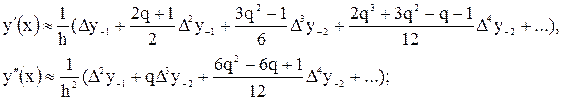 (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.8)
(3.8)
 . (3.9)
. (3.9) (3.10)
(3.10) .
. (3.6)
(3.6)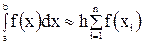 (3.7)
(3.7) (3.8)
(3.8) .
. (3.9)
(3.9) .
.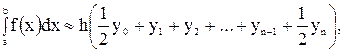 (3.10)
(3.10)
 ;
; (3.11)
(3.11)
 (3.12)
(3.12)

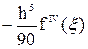


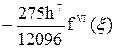


 (3.13)
(3.13)
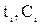 берутся из таблицы 3.2:
берутся из таблицы 3.2: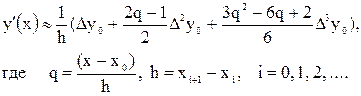 (3.14)
(3.14)

 и погрешность представления исходных данных ε является абсолютным числом обусловленности (nΔ) решения данной задачи численного дифференцирования. Его значение равно 280>>1, что свидетельствует о плохой обусловленности этой задачи.
и погрешность представления исходных данных ε является абсолютным числом обусловленности (nΔ) решения данной задачи численного дифференцирования. Его значение равно 280>>1, что свидетельствует о плохой обусловленности этой задачи. ,
,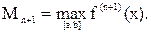
 .
.
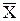 почти постоянно. Поэтому можно попытаться вычислить f¢(X) лишь однажды в точке
почти постоянно. Поэтому можно попытаться вычислить f¢(X) лишь однажды в точке  , а затем заменить f¢(
, а затем заменить f¢(


