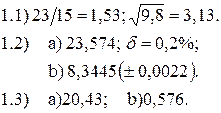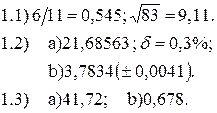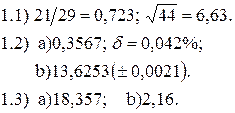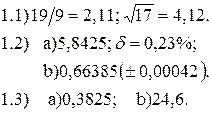Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
усовершенствованный метод ломаныхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для некоторого повышения точности решения задачи предыдущим методом сначала вычисляют промежуточные значения:
а затем находят
Усовершенствованный метод Эйлера-Коши
Сначала вычисляют «грубое» значение
которое затем уточняют по формуле
Погрешность метода на каждом шаге пропорциональна h3; Усовершенствованный метод Эйлера с уточнением
Сначала вычисляют
Итерации продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут. Погрешность метода на каждом этапе имеет порядок h3; Метод Рунге-Кутта
На каждом шаге вычисления выполняются по формуле где
Погрешность метода на каждом шаге имеет порядок Метод Адамса 7.1) формула с первыми конечными разностями:
Значение y1 находят любым другим способом, например, применяя метод Эйлера. Погрешность вычислений на каждом шаге имеет порядок h2. 7.2) формула со вторыми конечными разностями:
где
Значения y1 и y2 находят любыми другими способами. Погрешность на каждом шаге имеет порядок Метод Милна
Пусть для уравнений Последующие значения функции yi при i=4, 5, … определяются на каждом шаге следующим образом: для предсказания используется 1-я формула Милна:
Используя
Абсолютная погрешность 5.3. Пример решения типовой задачи Пусть необходимо решить, применяя метод Эйлера, следующее дифференциальное уравнение второго порядка: y¢¢-2y¢+sin(xy)+x=0, для которого заданы начальные условия: x0=0, y0=y(x0)=1, y¢0=y¢(x0)=1. Сначала необходимо понизить порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x,y)= y¢(x,y). Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1-го порядка:
P¢(x,y)=2P(x,y)-sin(xy)-x. Начальные условия для уравнений этой системы: x0=0, y0=1, Р0=1. Расчётные формулы для получения решения методом Эйлера имеют вид:
Pi+1=Pi+h×(2×Pi-sin(xi×yi) -xi). Последовательно подставляя в расчётные формулы начальные условия x0, y0 и Р0, а затем и вычисленные на очередном шаге значения xi, yi и Pi, можно получить численное решение исходного дифференциального уравнения второго порядка в виде табличного представления функции y(x) c заданным шагом h изменения аргумента х. Аналогичный приём понижения порядка дифференциальных уравнений может быть применён для произвольного ОДУ n-го порядка (число уравнений в соответствующей системе ОДУ 1-го порядка будет равно n). 5.4. Порядок выполнения работы 1. Изучить разделы 5.2 и 5.3 настоящих методических указаний. 2. Изучить обусловленные вариантом индивидуального задания методы решения предложенного дифференциального уравнения. 3. Записать расчетные формулы для решения поставленной задачи. 4. Разработать алгоритм и программу для построения таблицы значений искомой функции y(x) для уравнения, указанного в списке вариантов индивидуальных заданий (Приложение В, таблица B5.1), на заданном отрезке 5. Оценить точность полученного решения. 6. Составить отчет о проделанной работе.
5.5. Контрольные вопросы 1. Сформулируйте задачу Коши для обыкновенного дифференциального уравнения 1-го порядка. 2. Сформулируйте задачу Коши для обыкновенного дифференциального уравнения n-го порядка. 3. В чем состоит основная идея численного решения дифференциального уравнения, положенная в основу метода Эйлера? 4. Каковы достоинства и недостатки этого метода? Какова его погрешность? 5. В чем состоит основная идея численного решения дифференциального уравнения, положенная в основу метода Рунге-Кутта? 6. Какова погрешность решения для метода Рунге-Кутта? 7. Как может быть применена идея переменного шага для уменьшения погрешности решения и увеличения быстродействия при использовании этого метода? 8. Какие численные методы решения дифференциальных уравнений называются одношаговыми? Приведите примеры. 9. Какие численные методы решения дифференциальных уравнений называются многошаговыми? Приведите примеры. 10. В чем преимущество многошаговых методов по сравнению с одношаговыми? Недостатки? Библиографический список 1. Амосов А.А., Вычислительные методы для инженеров: Учебное пособие./А.А. Амосов, Ю.А.Дубинский, Н.В. Копченова. - М.: Изд-во МЭИ, 2003.-596с. 2. Бахвалов А.С. Численные методы в задачах и упражнениях. / А.С. Бахвалов. - М.: Высш. шк., 2000.-190с. 3. Бахвалов А.С. Численные методы. Учебное пособие./А.П. Жидков, Г.М. Кобельков. 4-е изд. М.-СПб.: Физматлит, Невский диалект, Лаборатория базовых знаний, 2003. - 624с. 4. Боглаев Ю.П. Вычислительная математика и программирование. / Ю.П. Боглаев. - М.: Высш. шк., 1990.-284с. 5. Волков Е.А. Численные методы./ Е.А. Волков. - М.: Наука, 1987. -248с. 6. Воробьева Г.А. Практикум по вычислительной математике. / Г.А.Воробьева, А.Н.Данилова. - М.: Высш. шк., 1990.-208с. 7. Демидович Б.П. Численные методы анализа. / Б.П.Демидович, И.А.Марон, Э.З.Шувалова. - М.: Наука, 1967.-534с. 8. Иванов В.В. Методы вычислений на ЭВМ. Справочное пособие./ В.В. Иванов. - К.: Наукова думка, 1986.-584с. 9. Самарский А.А. Задачи и упражнения по численным методам. / А.А. Самарский, П.Н. Вабищевич, Е.А. Самарская. - М.: Едиториал, 2003.-208с. ПРИЛОЖЕНИЯ ПРИЛОЖЕНИЕ А Образец оформления титульного листа отчета о выполнении лабораторной работы МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Севастопольский национальный технический университет
Кафедра кибернетики и вычислительной техники
ОТЧЁТ о выполнении лабораторной работы № х на тему: «ХХХХХХХХХХХХХХХХХХХХ» по дисциплине «Информатика и системология» № варианта хх
Выполнил: студент(ка) гр. ЭК- ХХ д Хххххххххх х.х. Проверила:
Севастополь ПРИЛОЖЕНИЕ В Варианты индивидуальных заданий для выполнения лабораторных работ
В1. Варианты индивидуальных заданий для выполнения лабораторной работы №1 «Исследование погрешностей результата вычислений при решении задач вычислительной математики» Задание 1. Для данных, представленных в таблице B1.1, выполнить следующее: 1.1. Определить какое равенство точнее. 1.2. Округлить сомнительные числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. 1.3. Найти предельные абсолютные и относительные погрешности, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле. Таблица B1.1.
Задание 2 2.1. Вычислить и определить погрешности результата вычислений выражения. Таблица B1.2
2.2. Вычислить выражение, пользуясь правилами подсчета цифр.
Таблица B1.3
В2. Варианты индивидуальных заданий для выполнения лабораторной работы №2 «Приближение функций» 2.1. Составить программу для нахождения приближенного значения функции при заданном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана: а) в неравноотстоящих узлах таблицы; б) в равноотстоящих узлах таблицы. Таблица B2.1.
2.2. Составить программу для вычисления приближенного значения функции при заданном значении аргумента с помощью интерполяционного многочлена Ньютона. Таблица B2.2
В3. Варианты индивидуальных заданий для выполнения лабораторной работы №3 «Численное дифференцирование и интегрирование» Таблица 3.1.
В таблице B3.1.использованы следующие коды методов: 1) для численного дифференцирования: 1-основанный на первой интерполяционной формуле Ньютона; 2- основанный на первой формуле Гаусса; 3-основанный на второй формуле Гаусса; 4-основанный на формуле Стирлинга; 5-основанный на формуле Бесселя; 2) численного интегрирования: 1-левых прямоугольников; 2-правых прямоугольников; 3-центральных (средних) прямоугольников; 4–Ньютона-Котеса; 5-трапеций; 6-Симпсона; 7-Гаусса. Таблица B3.2
В4. Варианты индивидуальных заданий для выполнения лабораторной работы №4 «Численное решение нелинейных уравнений»
Таблица B4.1.
В таблице B4.1 метод, соответствующий Вашему варианту, численного решения уравнения определяется следующим образом: 1. Метод простой итерации. 2. Метод Ньютона-Рафсона. Классический. 3. Метод Ньютона-Рафсона. Упрощенный. 4. Метод Ньютона-Рафсона. Метод ложных положений. 5. Метод секущих. 6. Метод половинного деления.
В5. Варианты индивидуальных заданий для выполнения лабораторной работы №4 «Численное решение дифференциальных уравнений»
Таблица B5.1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.012 с.) |

 ,
, . (5.8)
. (5.8) , (5.9)
, (5.9) . (5.10)
. (5.10) . (5.11)
. (5.11) , (5.12)
, (5.12) ,
,

 .
. ;
; (5.13)
(5.13) - конечная разность 1-го порядка.
- конечная разность 1-го порядка. , (5.14)
, (5.14) - конечная разность 1-го порядка,
- конечная разность 1-го порядка, - конечная разность 2-го порядка.
- конечная разность 2-го порядка.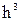 ;
;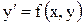 кроме начального условия
кроме начального условия  найден и некоторый «начальный отрезок», т.е. значения искомой функции
найден и некоторый «начальный отрезок», т.е. значения искомой функции  в точках
в точках  .
.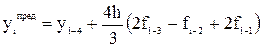 .
. , вычисляются
, вычисляются  и корректируются значения
и корректируются значения  по второй формуле Милна:
по второй формуле Милна: . (5.15)
. (5.15) значения
значения  приближенно определяется как
приближенно определяется как 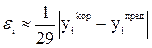 .
. y¢(x,y)=P(x,y)
y¢(x,y)=P(x,y) yi+1=yi+h×Pi
yi+1=yi+h×Pi с шагом h. Предусмотреть в программе вывод значений точного решения дифференциального уравнения с целью сравнения с полученными результатами.
с шагом h. Предусмотреть в программе вывод значений точного решения дифференциального уравнения с целью сравнения с полученными результатами. 1.2)
1.2) 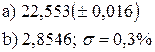 1.3)
1.3) 
 1.2)
1.2)  1.3)
1.3) 
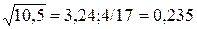 1.2)
1.2)  1.3)
1.3)