
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание классического метода Ньютона - РафсонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предположим, что уравнение f(X)=0 имеет один корень Возьмем некоторую точку начального приближения X0Î[a, b] и проведем в точке P0 {X0, f(X0)} касательную к кривой Y=f(X) до пересечения с осью OX. Абсциссу этой точки пересечения (X1) можно взять в качестве очередного приближенного значения корня. Проведя касательную через новую точку P1{X1, f(X1)} и находя точку ее пересечения с OX, получим второе приближение X2 к истинному положению корня и т. д. Уравнение касательной, проходящей через точку P0, имеет вид: Y=f(X0)+f¢(X0)(X–X0). Полагая Y=0, найдем абсциссу X1 точки пересечения касательной и OX
Следующие приближения найдем по формулам:
¼
Процесс вычисления приближений необходимо прекратить при выполнении условия:
где m1 – наименьшие значение |f¢(X)| на отрезке [a, b], M2 – наибольшее значение |f¢¢(X)| на том же отрезке. При этом будет выполняться равенство:
где e – предельная абсолютная погрешность корня Начальное приближение X0 выбирают так, чтобы было выполнено условие сходимости: f(X0)´f¢¢(X0)>0. (4.14) В противном случае не гарантируется сходимость метода. Чаще всего выбирают X0=a или X0=b в зависимости от того, в какой из точек выполняется условие сходимости.
Модификации метода Ньютона
Основным недостатком метода Ньютона является необходимость вычисления значения производной f¢(X) на каждой итерации. Рассмотрим некоторые модификации, лишенные этого недостатка. Заметим, что рассматриваемые ниже итерационные методы решения нелинейного уравнения на каждой итерации используют процедуру его линеаризации, то есть исходное нелинейной уравнение заменяется приближенно более простым линейным уравнением. -Упрощенный метод Ньютона Если производная функции f¢(X) непрерывна, то ее значение вблизи простого корня
Упрощения вычислений по сравнению с методом Ньютона достигается ценой резкого падения скорости сходимости. Сходимость этого метода является уже не квадратичной, а линейной. Этот метод можно рассматривать как метод простой итерации с итерационной функцией:
Так как
то для знаменателя q соответствующей геометрической прогрессии имеем:
Следовательно, скорость сходимости тем выше, чем ближе начальное приближение
-Метод ложного положения В основе этой и следующей модификаций метода Ньютона лежит приближенное равенство:
Оно верно при условии известности Zn и Xn и следует из определения производной:
Пусть C - фиксированная точка, расположенная в окрестности простого корня`X. Заменим в расчетной формуле классического метода Ньютона
производную правой частью формулы (4.19), полагая, что Zn=C. В результате приходим к формуле ложного положения:
Метод обладает линейной сходимостью. Его можно рассматривать как метод простой итерации с итерационной функцией:
Так как скорость сходимости определяется вблизи корня величиной
то она тем выше, чем ближе окажется выбранная точка C к корню уравнения.
- Метод секущих
Замена в формуле (4.12) для метода Ньютона производной f¢(X) приближением:
приводит к расчетной формуле для метода секущих:
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

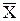 на интервале [a, b], производные f¢(X) и f¢¢(X) определены, непрерывны и сохраняют постоянные знаки на отрезке [a, b].
на интервале [a, b], производные f¢(X) и f¢¢(X) определены, непрерывны и сохраняют постоянные знаки на отрезке [a, b].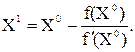

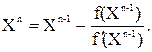 (4.12)
(4.12) (4.13)
(4.13)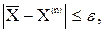
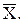
 , а затем заменить f¢(
, а затем заменить f¢(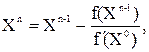 n³0. (4.15)
n³0. (4.15) (4.16)
(4.16)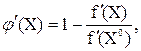 (4.17)
(4.17) (4.18)
(4.18) (4.19)
(4.19) (4.20)
(4.20)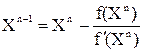
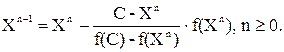 (4.21)
(4.21) (4.22)
(4.22)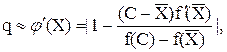 (4.22)
(4.22)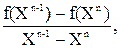
 (4.23)
(4.23)


