
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщение полюсного метода Ньютона на многомерный случайСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Переложим вывод одномерного полюсного метода Ньютона (5.36) на векторную основу. Будем при этом руководствоваться геометрическими соображениями, опирающимися на рис. 5.12, и пользоваться теми же обозначениями. Касательную к кривой
Первое из этих условий означает равенство нулю скалярного произведения (n,u), второе — пропорциональность соответствующих координат векторов v и l или, иначе, равенство нулю составленного из них определителя. Следовательно, искомое приближение
(вторая компонента — ордината точки пересечения указанных прямых — после вычисления значения Рассмотренный векторный подход к построению одномерного полюсного метода Ньютона служит ключом для его распространения на двумерный случай на основе таких же геометрических, но уже пространственных соображений. Пусть требуется найти приближенное решение двумерной нелинейной системы (4.3.1) в предположении непрерывной дифференцируемости входящих в нее функций f(x, у) и g(x, у) в некоторой области G, содержащей искомое решение х* =(х*; у*) и приближения к нему Будем считать, что уже найдено k-е приближение к решению х* и нужно получить правило перехода к (k+1)-му приближению. В сделанном предположении о гладкости функций f(x, у) и g(x, у) можно провести касательные плоскости в точке ( z = f(x,y) и z = g(x,y). (3.5.3) Эти плоскости задаются текущими векторами
и нормалями
соответственно, т.е. аналогично первому из условий (3.5.1) должно быть
Пересечение двух касательных плоскостей, т.е. образ, определяемый уравнениями (3.5.4), есть прямая в трехмерном пространстве, общая точка которой с координатной плоскостью Оху является ньютоновским приближением Чтобы осуществить поставленную цель, зафиксируем в R3 две несовпадающие между собой и с Запишем совокупность всех трех описанных средствами векторной алгебры плоскостей в координатной форме. Имеем:
Первые две координаты вектора (x;y;z), служащего решением полученной системы уравнений, считаем искомым приближением (
эту систему превращаем в систему уравнений относительно неизвестных
Для исключения вспомогательной переменной z из линейной системы (3.5.6) выразим ее из третьего уравнения. Обозначив
раскрываем фигурирующий в (3.5.6) определитель по элементам первой строки:
Отсюда находим выражение
подставляя которое в первые два уравнения системы (3.5.6), приходим к двумерной линейной системе
Фактически эта система вместе с обозначениями (3.5.7) и определяет двумерный полюсный метод Ньютона для нелинейной системы (4.3.1). Надя их нее поправки
Дельнейшее преобразование полюсного метода Ньютона, т. е. переход от размерности 2 к произвольной размерности, совершаем формально на основе предыдущего построения. Пусть задана нелинейная система, функции
где Зададим n полюсов
Векторно-матричное уравнение (3.5.10) и скалярное уравнение (3.5.11), в принципе, уже определяют векторный n-полюсный метод Ньютона для построения приближенной к решению системы. Чтобы записать соответствующую линейную систему относительно поправок
(аналогичную схеме (3.5.9) двумерного случая), введем следующие обозначения. Положим
и образуем квадратную (n+1)-мерную матрицу следующей структуры:
Тогда на основе (3.5.10), (3.5.11) имеем (n +1)-мерную систему уравнений относительно неизвестных
Как и в двумерном случае, из второго уравнения этой системы выражаем вспомогательную неизвестную
где Заменив в (3.5.13) все компоненты вектора z найденным их значением (3.5.14), приходим к следующему линейному векторно матричному уравнению относительно вектора-поправки
где
Уравнение (3.5.15) вместе со связью (3.5.12), согласно которой
является неявной формой п -полюсного метода Ньютона для уравнения (2.1а). Совокупности формул (3.5.15)-(3.5.17) можно придать другой вид:
который удобно трактовать как явный метод Ньютона со своеобразной коррекцией матриц Якоби путем прибавления к ним формирующихся по заданному правилу матриц
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.132.71 (0.009 с.) |

 в точке (
в точке ( ) зададим условием ортогональности текущего вектора
) зададим условием ортогональности текущего вектора  этой прямой и ее нормального вектора, в качестве которого можно взять вектор
этой прямой и ее нормального вектора, в качестве которого можно взять вектор  . Уравнение прямой, проходящей через полюс
. Уравнение прямой, проходящей через полюс  и связанную с уже известным приближением
и связанную с уже известным приближением  точку (
точку ( ), получим из условия коллинеарности текущего вектора этой прямой
), получим из условия коллинеарности текущего вектора этой прямой  и ее направляющего вектора
и ее направляющего вектора  . Таким образом, точку пересечения двух прямых, проекцию которой на ось абсцисс считаем новым приближением
. Таким образом, точку пересечения двух прямых, проекцию которой на ось абсцисс считаем новым приближением  , находим из совокупности условий
, находим из совокупности условий
 (3.5.1)
(3.5.1) (3.5.2)
(3.5.2)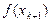 может дать информацию об отклонении от функции
может дать информацию об отклонении от функции  в точке
в точке  тождественно его выражению по формуле (5.36).
тождественно его выражению по формуле (5.36). k = 0,1,2,....
k = 0,1,2,.... ) определяемым ими поверхностям
) определяемым ими поверхностям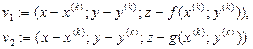


 иначе,
иначе, .
.  (3.5.4)
(3.5.4) к решению х* сиcтемы (4.3.1). Наша цель — построить третью плоскость, пересечение которой с упомянутой прямой (линией пересечения касательных плоскостей) давало бы точку в пространстве R3 такую, проекция которой на плоскость Оху могла бы оказаться ближе к х*, чем
к решению х* сиcтемы (4.3.1). Наша цель — построить третью плоскость, пересечение которой с упомянутой прямой (линией пересечения касательных плоскостей) давало бы точку в пространстве R3 такую, проекция которой на плоскость Оху могла бы оказаться ближе к х*, чем  точки — полюсы
точки — полюсы 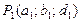 и
и  . Через указанные три точки
. Через указанные три точки  можно провести единственную плоскость (которая здесь играет роль прямой, проходящей через полюс и точку (хк; 0) в одномерной ситуации). Взяв текущую точку М(х; у; z) и образовав текущий вектор
можно провести единственную плоскость (которая здесь играет роль прямой, проходящей через полюс и точку (хк; 0) в одномерной ситуации). Взяв текущую точку М(х; у; z) и образовав текущий вектор  этой третьей плоскости, можно задать ее условием компланарности трех векторов-
этой третьей плоскости, можно задать ее условием компланарности трех векторов-  и
и  (что служит аналогом второго из условий (3.5.1)).
(что служит аналогом второго из условий (3.5.1)).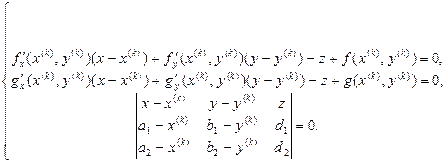
 ).Введя поправки
).Введя поправки ,
,  (3.5.5)
(3.5.5) и z:
и z: (3.5.6)
(3.5.6) ,
,  ,
,  (3.5.7)
(3.5.7)
 (3.5.8)
(3.5.8) (3.5.9)
(3.5.9) :
: ,
,  .
. (образующими вектор
(образующими вектор  ) в точке
) в точке  , можно описать матрично-векторным уравнением
, можно описать матрично-векторным уравнением , (3.5.10)
, (3.5.10) - n-мерный вектор, каждой компонентой которого служит вспомогательная переменная
- n-мерный вектор, каждой компонентой которого служит вспомогательная переменная  , входящая в уравнения гиперповерхностей
, входящая в уравнения гиперповерхностей  .
.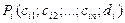 (i=1,2,…,n) так, чтобы они не принадлежали одной гиперплоскости пространства
(i=1,2,…,n) так, чтобы они не принадлежали одной гиперплоскости пространства  . Через все эти полюсы
. Через все эти полюсы  и точку (
и точку (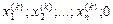 ), определяемую известным приближением
), определяемую известным приближением  к решению системы, проводим гиперплоскость, уравнение которой аналогично двумерному случаю задаем условием равенство нулю определителя (n+1) порядка:
к решению системы, проводим гиперплоскость, уравнение которой аналогично двумерному случаю задаем условием равенство нулю определителя (n+1) порядка: . (3.5.11)
. (3.5.11) (3.5.12)
(3.5.12) ,
,  ,
, 
 .
. :
: (3.5.13)
(3.5.13) (3.5.14)
(3.5.14) , а
, а  есть алгебраические дополнения к элементам
есть алгебраические дополнения к элементам  первой строки матрицы
первой строки матрицы  (что через соответствующие миноры
(что через соответствующие миноры  этой матрицы можно представить так:
этой матрицы можно представить так:  ,
,  ).
). :
: , (3.5.15)
, (3.5.15) . (3.5.16)
. (3.5.16) , (3.5.18)
, (3.5.18)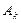 . Как и в одномерном случае, для ускорения сходимости последовательности приближений
. Как и в одномерном случае, для ускорения сходимости последовательности приближений  целесообразно изменять в такт с изменением значений функций, и в самом простом случае есть смысл фиксировать матрицу С, а вектор
целесообразно изменять в такт с изменением значений функций, и в самом простом случае есть смысл фиксировать матрицу С, а вектор  брать равным
брать равным  или -
или - 


