
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна та програмна реалізація метода ЗейделяСодержание книги
Поиск на нашем сайте
(для системи 3-х нелінійних рівнянь з трьома невідомими)
… Var E,x1,x2,x3,F1,F2,F3, x11,x21,x31:real; k: integer; Label M,M1; … Begin <введення вихідних даних > K:=0; M1: x11:=-x1*x1+2*x2*x3+0.1; X21:=x2*x2-3*x11*x3-0.2; X31:=-x3*x3-2*x11*x21+0.3; F1:=x11+x11*x11-2*x21*x31-0.1; F2:=x21-x21*x21+3*x11*x31+0.2; F3:=x31+x31*x31+2*x11*x21-0.3; if (abs(F1)<=E) and (abs(F2)<=E) and (abs(F3)<=E) then goto M; x1:=x11; x2:=x21; x3:=x31; k:=k+1; goto M1; M: <виведення результатів> …
Примітки: 1. Фрагмент програми реалізує розв’язання системи рівнянь, яка розглянута у прикладі; 2. Вихідними даними є початкові наближення коренів 3. Результат обчислень - наближення коренів із заданою точністю х11,х21,х31, точність 4. Ітераційний процес закінчується, коли нев’язки всіх рівнянь стануть меншими за задану точність
Порядок виконання роботи
1. Вибрати індивідуальне завдання. Номер варіанту в Таблиці 4.1. відповідає номеру студента у списку групи; 2. Ознайомитись з теоретичним матеріалом по чисельним методам розв’язання СНАР; 3. Виконати «ручне» розв’язання заданої системи рівнянь методом Зейделя з точністю ε = 0.01 (до 4-х ітерації); 4. Скласти докладний алгоритм розв’язання заданої СНАР методом Зейделя; 5. Скласти і відлагодити програму на мові Pascal, яка реалізує введення вихідних даних, розв’язання заданої системи рівнянь методом Зейделя, виведення результатів на екран і у файл в зручній формі. Основні фрагменти програми оформити як процедури і функції; 6. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 7. Розв’язати задану СНАР за допомогою розробленої програми, порівняти отримані результати із результатами ручних розрахунків. Побудувати графіки збіжності ітераційного процесу: 8. Обчислити корені системи рівнянь при 5 різних значеннях точності 9. Внести зміни у програму відповідно до алгоритму метода ітерації і розв’язати задану СНАР. Побудувати графіки збіжності ітераційного процесу. Порівняти отримані результати із результатами п.7; 10. Підготувати висновки по роботі.
Результати виконання кожного пункту викласти у звіті по роботі. Для отримання підвищеної оцінки необхідно розробити власну програму на основі наведеного фрагменту.
Таблиця 4.1. Варіанти завдань до Занять №4 і №5
Заняття № 5 Розробка програми Розв’язання системи нелінійних алгебраїчних рівнянь Методом Ньютона-Рафсона Мета роботи: Закріплення знань із застосування ітераційного метода Ньютона-Рафсона для чисельного розв’язання СНАР, вивчення алгоритму метода, розробка відповідної комп’ютерної програми на мові Pascal і застосування її для розв’язання заданої системи рівнянь.
Теоретичні відомості Метод Ньютона-Рафсона для розв’язання СНАР Метод має відносно нескладний алгоритм обчислень і забезпечує швидку збіжність ітераційного процесу, яка мало залежить від розмірності задачі. Суть методу полягає у послідовній заміні на кожній ітерації розрахунку вихідної нелінійної системи рівнянь допоміжною лінійною, розв’язання якої дозволяє визначити чергові наближення невідомих (лініаризація). Відмінність методу Ньютона-Рафсона для розв’язання систем нелінійних рівнянь від методу Ньютона для розв’язання окремих нелінійних рівнянь полягає в переході від одномірної задачі до багатовимірної. Замість однієї невідомої величини
Рекурентна формула, що дозволяє визначити наступне наближення невідомих за методом Ньютона-Рафсона, по структурі подібна до (1.4), але включає, як складові, об’єкти (5.1):
Тут
Елементами матриці Якобі є частинні похідні від всіх рівнянь системи, записаної у формі (4.1), по всім невідомим. Кожний і -й рядок матриці складається із похідних від одного і - го рівняння вихідної системи. Розмірність матриці Якобі
Визначення наближень невідомих за формулою (5.2) ускладнюється необхідністю обернення матриці Якобі на кожній ітерації розрахунку, особливо якщо вона має велику розмірність. Тому, часто для обчислення наступного наближення невідомих в методі Ньютона-Рафсона формують і розв’язують допоміжну систему лінійних рівнянь відносно поправок до невідомих величин. Ця система утворюється із (5.2) і має вигляд:
Система (5.3) лінійна відносно невідомих поправок
Нові наближення невідомих використовуються для обчислень на наступній ітерації і послідовного уточнення коренів вихідної системи нелінійних рівнянь. Послідовність дій при розв’язанні СНАР методом Ньютона-Рафсона а) Підготовчий етап: 1. Перетворення вихідної системи нелінійних рівнянь у форму (4.1); 2. Визначення аналітичних виразів частинних похідних від усіх рівнянь системи по всім невідомим диференціюванням відповідних рівнянь 3. Визначення структури вектора поправок невідомих 4. Формування допоміжної лінійної (лініаризованої) системи рівнянь подібно (5.3). У загальному вигляді її можна записати:
б) Розв’язання системи рівнянь: 5. Вибір початкового наближення невідомих 6. Підстановка чергових наближень коренів (на 1-й ітерації – це початкові наближення) у вихідну систему рівнянь (4.1) і визначення нев’язок рівнянь 7. Підстановка вибраних наближень коренів у виразі частинних похідних від рівнянь системи 8. Формування лініаризованої системи рівнянь (5.5); 9. Розв’язання цієї системи будь-яким методом і визначення поправок до невідомих 10. Обчислення наступних наближень коренів за формулою (5.4); 11. Контроль завершення ітераційного процесу за умовами досягнення заданої точності
Приклад розв’язання СНАР методом Ньютона-Рафсона Визначити корні системи 3-х нелінійних рівнянь з трьома невідомими. Точність
Система у формі (4.1):
Визначаємо частинні похідні від рівнянь системи
Формуємо матрицю Якобі:
Формуємо лініаризовану систему рівнянь:
Вибираємо початкові наближення невідомих:
Ітерація 1. Підставляємо початкові наближення у матрицю Якобі і вектор нев’язок, обчислюємо значення їх елементів. Тоді лініаризована система рівнянь набуває вигляду:
Розв’язавши її, визначаємо вектор поправок до невідомих:
Знаходимо наступні наближення коренів:
Нев’язки рівнянь при цих наближеннях:
Нев’язки рівнянь
Ітерація 2. Підставляємо знайдені наближення коренів у матрицю Якобі і вектор нев’язок і обчислюємо значення їх елементів:
Лініаризована система рівнянь набуває вигляду:
Розв’язуємо отриману систему лінійних рівнянь і визначаємо чергове наближення вектора поправок до невідомих:
Наступні наближення коренів нелінійної системи рівнянь:
Нев’язки рівнянь системи при цих наближеннях:
Нев’язки
5.2. Алгоритмічна та програмна реалізація метода Ньютона-Рафсона (для системи 3-х нелінійних рівнянь з трьома невідомими)
Var E: real; k,i:integer; x0,x,F,Dx: array [1..3] of real; DF: array [1..3,1..3] of real; Label M,M1; Procedure FUNKC; Begin F[1]:=x[1]+x[1]*x[1]-2*x[2]*x[3]-0.1; F[2]:=x[2]+x[2]*x[2]+3*x[1]*x[3]+0.2; F[3]:=x[3]+x[3]*x[3]+2*x[1]*x[2]-0.3; End; Begin <введення вихідних даних> k:=0; for i:=1 to 3 do x[i]:=x0[i]; FUNKC; M1: DF[1,1]:=1+2*x[1]; DF[1,2]:=-2*x[3]; DF[1,3]:=-2*x[2]; DF[2,1]:=3*x[3]; DF[2,2]:=1-2*x[2]; DF[2,3]:=3*x[1]; DF[3,1]:=2*x[2]; DF[3,2]:=2*x[1]; DF[3,3]:=1+2*x[3]; GAUSS(DF,F,Dx); for i:=1 to 3 do x[i]:=x[i]+Dx[i]; FUNKC; if (F[1]<=E) and (F[2]<=E) and (F[3]<=E) then goto M; k:=k+1; goto M1; M: <виведення результатів> …
Примітки: 1. Програма реалізує розв’язання нелінійної системи рівнянь, яка розглянута у прикладі; 2. Для розв’язання лініаризованої системи рівнянь можна використати процедуру GAUSS, яка реалізує метод Гауса і розроблена на занятті № 2; 3. Процедура FUNKC обчислює нев’язки рівнянь системи при чергових значеннях наближень невідомих; 4. Використовуються масиви: x0 i x - вектори початкових і чергових наближень невідомих, F - вектор нев’язок рівнянь, Dx - вектор поправок до невідомих, DF - матриця Якобі.
Порядок виконання роботи
Виконати пункти 1…8 і п.10 завдання Заняття № 4 (розділ 4.3), застосувавши для розв’язання заданої СНАР метод Ньютона-Рафсона. Порівняти методи розв’язання СНАР.
Результати виконання кожного пункту завдання викласти у звіті по роботі. Для отримання підвищеної оцінки необхідно розробити власну програму на основі наведеного фрагменту. Заняття № 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.2 (0.009 с.) |


 і точність обчислень
і точність обчислень 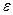 ;
; ;
; . Результати оформити у вигляді таблиці;
. Результати оформити у вигляді таблиці;

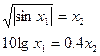


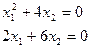









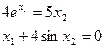











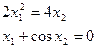




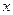 , нев’язки одного рівняння
, нев’язки одного рівняння 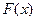 і похідної від цього рівняння
і похідної від цього рівняння  розглядаємо відповідно вектор невідомих
розглядаємо відповідно вектор невідомих  , вектор нев’язок рівнянь системи
, вектор нев’язок рівнянь системи  і матрицю частинних похідних від рівнянь системи по всім невідомим (матриця Якобі)
і матрицю частинних похідних від рівнянь системи по всім невідомим (матриця Якобі)  :
: (5.1)
(5.1)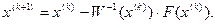 (5.2)
(5.2) - вектори чергового к -го і наступного ( к+1 )- го наближень невідомих;
- вектори чергового к -го і наступного ( к+1 )- го наближень невідомих; -вектор нев’язок рівнянь вихідної системи при черговому наближенні
-вектор нев’язок рівнянь вихідної системи при черговому наближенні  ;
; - матриця Якобі при черговому наближенні невідомих
- матриця Якобі при черговому наближенні невідомих 
 , (5.3) де
, (5.3) де  = x(k+1) – x(k).
= x(k+1) – x(k). . В ній елементи матриці Якобі
. В ній елементи матриці Якобі 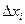 . Розв’язавши цю систему будь-яким методом, визначаємо елементи вектора поправок
. Розв’язавши цю систему будь-яким методом, визначаємо елементи вектора поправок  (5.4)
(5.4) .
. , вектора нев’язок
, вектора нев’язок  , і матриці Якобі
, і матриці Якобі  для заданої системи рівнянь;
для заданої системи рівнянь;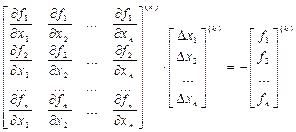 (5.5)
(5.5)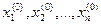 (наприклад так, як зроблено у Занятті № 4);
(наприклад так, як зроблено у Занятті № 4); при цих наближеннях;
при цих наближеннях; і обчислення їх значень при чергових наближеннях. Формування матриці Якобі;
і обчислення їх значень при чергових наближеннях. Формування матриці Якобі;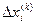 ;
; є розв’язком нелінійної системи рівнянь із заданою точністю
є розв’язком нелінійної системи рівнянь із заданою точністю 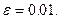
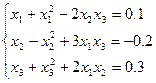

 по всім невідомим
по всім невідомим  :
: .
.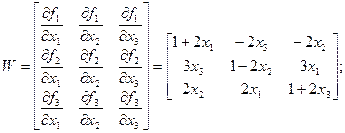

 .
.



 тому виконуємо наступну ітерацію.
тому виконуємо наступну ітерацію.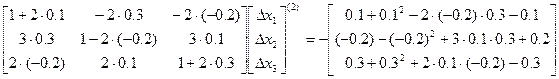


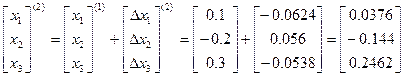

 - умови завершення ітераційного процесу виконуються не для всіх рівнянь, тому необхідні наступні ітерації.
- умови завершення ітераційного процесу виконуються не для всіх рівнянь, тому необхідні наступні ітерації. …
…


