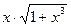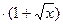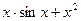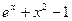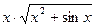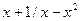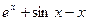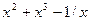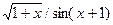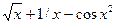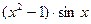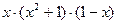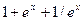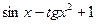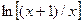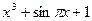Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розробка програми чисельного інтегрування функцій методом трапеційСодержание книги
Поиск на нашем сайте
Мета роботи: Закріплення знань із застосування методів чисельного інтегрування функцій, розробка відповідного алгоритму і програми на мові Pascal і застосування її для розв’язання індивідуального завдання. Теоретичні відомості У загальному випадку звичайний визначений інтеграл безперервної функції
де Він дорівнює площі фігури, обмеженої прямими x = a та x = b, віссю абсцис Х і кривою підінтегральної функції f
I
0 x0=a xn=b x
Чисельне інтегрування застосовується, коли визначення функції F(x) неможливе, або воно дуже складне, коли функція Тоді приблизно приймається, що Суть методів чисельного інтегрування полягає в тому, що інтервал інтегрування [ a, b ] розбивається на n менших відрізків, на кожному з яких підінтегральна крива
Формула трапецій Виконується лінійна апроксимація функції
Кожний відрізок обмежується рівновіддаленими точками хi Крива у = c y=f(x) При малому h площа під кривою B E
A D xi xi+1 h
Наближене значення інтегралу І дорівнює сумі площ n таких елементарних трапецій:
Наближене значення інтегралу І дорівнює сумі площ n таких елементарних трапецій: 0 Тут h – крок інтегрування, визначається за формулою (7.2);
Геометрично формула трапецій (7.3) відповідає заміні графіка підінтегральної функції y= Точність результату збільшується при збільшенні кількості відрізків розбиття n.
Приклад обчислення інтегралу за формулою трапецій
Підінтегральна функція Розбиваємо інтервал інтегрування на n =10 відрізків:
Обчислюємо значення підінтегральної функції в точках розбиття хі, і =0,…,10:
Обчислюємо наближене значення інтегралу за формулою трапецій:
Точне значення інтегралу дорівнює 1.3987. Похибка інтегрування складає 0.021%. Алгоритмічна та програмна реалізація методу трапецій
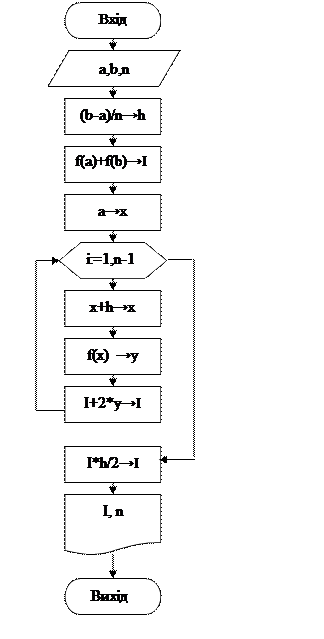
i,n: integer; Begin <Введення вихідних данних> H:=(B-A)/n; I:=sqrt(1+2*A)+sqrt(1+2*B); X:=A; For i:=1 to n-1 do Begin X:=X+H; Y:=sqrt(1+2*X); I:=I+2*Y; End; I:=I*H/2; <Виведення результатів> … Примітки: 1. В програмі реалізоване обчислення інтегралу, що розглянутий у прикладі; 2. Якщо функція
Порядок виконання роботи 1. Вибрати індивідуальне завдання. Номер варіанту у таблиці 7.1. відповідає номеру студента в списку групи; 2. Ознайомитись із теоретичним матеріалом з питань чисельного інтегрування функцій; 3. Обчислити наближене значення заданого інтегралу методом трапецій при n =10; 4. Скласти докладний алгоритм чисельного інтегрування функцій методом трапецій; 5. Скласти і відлагодити програму на мові Pascal, яка реалізує: - введення вихідних даних; - обчислення значень підінтегральної функції у визначених точках; - обчислення заданого інтегралу методом трапецій; - виведення результатів у зручній формі. Основні фрагменти програми оформити як процедури і функції; 6. Описати розроблений алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 7. З використанням розробленої програми обчислити заданий інтеграл при n =10. Порівняти отримані результати з результатами ручних розрахунків (п.3); 8. Обчислити значення заданого інтегралу при n =20, 30, 40, …, 100. Результати показати у вигляді таблиці на екрані і в файлі; 9. Сформулювати висновки по роботі.
Результати виконання кожного пункту завдання докладно описати у звіті по роботі.
Таблиця 7.1. Варіанти завдань до занять №7 і №8
Заняття № 8 Розробка програми
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.128.55 (0.008 с.) |

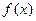 на відрізку [ a, b ] можна обчислити за формулою Ньютона-Лейбніца:
на відрізку [ a, b ] можна обчислити за формулою Ньютона-Лейбніца: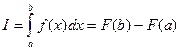 , (7.1)
, (7.1)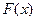 - першообразна функції
- першообразна функції 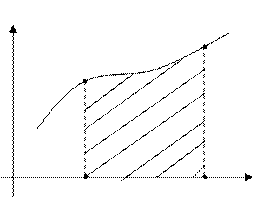
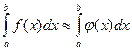 .
. 
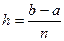 (7.2)
(7.2)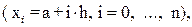 значення підінтегральної функції
значення підінтегральної функції 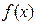 в яких
в яких 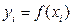 задані, або їх можна обчислити.
задані, або їх можна обчислити.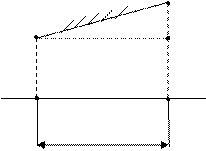 (хі – хі+1) замінюється прямою ВС.
(хі – хі+1) замінюється прямою ВС.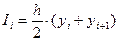 трапеції ABCD: yi yi+1
трапеції ABCD: yi yi+1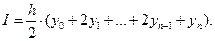 (7.3)
(7.3)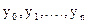 - значення підінтегральної функції
- значення підінтегральної функції 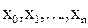 .
.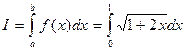
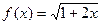 ; a=0; b=1.
; a=0; b=1.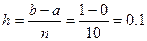
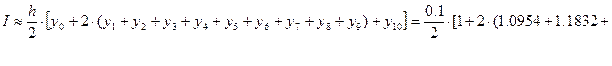
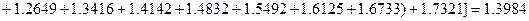
 Var A,B,X,Y,I,H: real;
Var A,B,X,Y,I,H: real;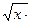 (2+sin2 x)
(2+sin2 x)