
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна та програмна реалізація градієнтного методуСодержание книги
Поиск на нашем сайте
Var x,x0,F,F1,E,h: real; k:=integer; begin <введення вихідних даних> k:=0; x:=0; Repeat F:=0.1*x*sqr(x)-2*x*x+10*x; F1:=0.3*x*x-4*x+10; x:=x+h*F1; <виведення k, x, F, F1> k:=k+1; Until abs(F1)<=E; End.
Примітки: 1. У програмі реалізовано визначення максимуму функції, яка розглянута у прикладі; 2. Розглядається функція однієї змінної. Тому
Порядок виконання роботи 1. Вибрати індивідуальне завдання. Номер варіанту в таблиці 12.1. відповідає номеру студента у списку групи; 2. Ознайомитись з теоретичним матеріалом з питань визначення екстремумів функцій і оптимізації; 3. Градієнтним методом виконати 5 кроків у напрямку шуканого екстремуму заданої функції. Коефіцієнт кроку 4. Скласти докладний алгоритм пошуку екстремумів функцій градієнтним методом; 5. Скласти і відлагодити програму на мові програмування Pascal, яка реалізує: · введення вихідних даних; · пошук екстремуму заданої функції градієнтним методом; · виведення результатів на екран і в файл; · виведення ходу оптимізації на екран в графічній формі. Основні фрагменти програми реалізувати як процедури і функції; 6. Описати алгоритм і програму (змінні, масиви, процедури і функції тощо); 7. З використанням розробленої програми визначити екстремум заданої функції 8. З використанням розробленої програми побудувати графік заданої функції 9. Побудувати на екрані ПК графіки, що ілюструють хід оптимізації по кроках · траєкторія спуску до екстремуму заданої функції · зміна значень функції по кроках · зміна довжини вектора-градієнта по кроках 10. Дослідити вплив значення коефіцієнту кроку 11. З використанням програми обчислити інші екстремуми функції 12. Сформулювати висновки по роботі. Результат виконання кожного пункту завдання докладно описати у звіті по роботі. Використання без змін в розробленій програмі фрагменту, наведеного у п. 12.2., заслуговує на мінімальну оцінку. Для отримання підвищеної оцінки необхідно розробити власний варіант програми.
Таблиця 12.1. Варіанти завдань до заняття № 12
Список літератури 1. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966. 2. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977. 3. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. – М.: Наука, 1989. – 240 с. 4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. – М.: Наука, 1972. – 576 с. 5. Бородич Ю.С., Вальвачев А.Н., Кузмич А.И. Паскаль для персональных компьютеров.- М.: Наука, 1994.- 200 с. 6. Довгаль С.И., Сбитнев А.И. Паскаль, ТурбоПаскаль, многооконная среда на персональных ЭВМ. – К.: Информсистема- сервис, 1992. – 181 с. Зміст Вступ 3 Заняття № 1. Розробка програми розв’язання нелінійних рівнянь методом Ньютона 4
Заняття № 2. Розробка програми розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) методом Гауса 11 Заняття № 3. Розробка програми розв’язання СЛАР методом подвійної факторизації 22 Заняття № 4. Розробка програми розв’язання системи нелінійних алгебраїчних рівнянь (СНАР) методом Зейделя 32 Заняття № 5. Розробка програми розв’язання системи нелінійних алгебраїчних рівнянь методом Ньютона-Рафсона 39 Заняття № 6. Розробка програми інтерполяції функцій 46 Заняття № 7. Розробка програми чисельного інтегрування функцій методом трапецій 53 Заняття № 8. Розробка програми чисельного інтегрування функцій методом Симпсона 57 Заняття № 9. Розробка програми чисельного диференціювання Функцій 60 Заняття № 10. Розробка програми чисельного розв’язання звичайних диференційних рівнянь (ЗДР) методом Ейлера 64
Заняття № 11. Розробка програми чисельного розв’язання ЗДР методом Рунге-Кутта четвертого порядку 72 Заняття № 12. Розробка програми визначення екстремумів функцій градієнтним методом 75 Список літератури 81
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.154.86 (0.009 с.) |

 Program Grad;
Program Grad;

 вибрати самостійно;
вибрати самостійно; і відповідне значення параметру
і відповідне значення параметру  з точністю
з точністю  . Порівняти з результатами п.3;
. Порівняти з результатами п.3;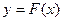 на вибраному самостійно інтервалі [a;b]. Показати на ньому знайдений екстремум функції
на вибраному самостійно інтервалі [a;b]. Показати на ньому знайдений екстремум функції  і відповідне значення
і відповідне значення 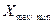 ;
; :
: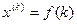 ;
; ;
;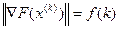 ;
; ;
;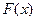

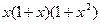
















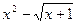

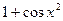




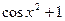



 +х
+х



