
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельного розв’язання звичайних диференційних рівнянь (ЗДР)Содержание книги
Поиск на нашем сайте
методом Ейлера Мета роботи: Закріплення знань із застосування чисельних методів розв’язання ЗДР і використання для цього методів Ейлера, розробка відповідного алгоритму і програми на мові Pascal, застосування її для розв’язання заданого диференційного рівняння. Теоретичні відомості Диференційним називається рівняння, яке зв’язує незалежну змінну
Порядок рівняння визначається найвищою похідною у його складі. Якщо функція У роботі розглядаємо звичайні диференційні рівняння першого порядку:
або Розв’язком, або інтегралом диференційного рівняння називається будь-яка функція Загальним розв’язком диференційного рівняння першого порядку називається функція:
яка залежить від однієї довільної постійної величини 1. Вона є розв’язком диференційного рівняння при будь-якому конкретному значенні 2. При будь-якій початковій умові Графічно, загальному розв’язку ЗДР відповідає сімейство кривих, що описується рівнянням (10.3) при різних значеннях Частковим розв’язком називається функція Розв’язати (проінтегрувати) диференційне рівняння означає визначити його частковий розв’язок, що відповідає заданим початковим умовам. Розв’язок отримаємо у вигляді функції Чисельні методи розв’язання ЗДР застосовуються тоді, коли коефіцієнти і функції в рівнянні занадто складні або задані у табличній формі, що унеможливлює розв’язання таких рівнянь класичними аналітичними методами. Одним із широких класів чисельних методів розв’язання диференційних рівнянь є методи Рунге-Кутта. Це одноступеневі методи, в яких для обчислення значення функції
В даній роботі використовуємо деякі із методів цього класу - метод Ейлера, виправлений метод Ейлера і модифікований метод Ейлера.
Методи Ейлера для чисельного розв’язання ЗДР Треба визначити наближений розв’язок рівняння
на відрізку Ділимо відрізок
Тоді
Відповідно до методу Ейлера наближені значення функції
Тут Метод має велику похибку і часто виявляється нестійким.
У виправленому методі Ейлера (метод трапецій) для обчислення значень функції
де
Модифікований метод Ейлера дозволяє обчислити значення
де
Метод Ейлера відноситься до методів Рунге-Кутта першого порядку, виправлений і модифікований методи Ейлера - до методів Рунге-Кутта другого порядку. Порядок методу визначається порядком
Існує загальна форма запису методів Ейлера:
При w =0 отримуємо метод Ейлера (формула (10.6)), w =0.5 - метод трапецій (формула (10.7)), при w =1 - модифікований метод Ейлера (формула 10.8). Приклад розв’язання диференційного рівняння методами Ейлера Визначити наближене розв’язання диференційного рівняння 1-го порядку Відповідно до (10.4) в цьому рівнянні права частина:
Ділимо відрізок [ 0;1 ] на Для розв’язання рівняння треба обчислити значення Метод Ейлера. Застосовуємо формулу (10.6). Для заданого рівняння вона набуває вигляду:
Результати обчислень запишемо у таблицю:
Отримали наближені значення функції
Похибка складає Виправлений метод Ейдера. Застосовуємо формулу (10.7). Вона набуває вигляду:
Результат обчислень запишемо у таблицю:
Похибка Модифікований метод Ейлера. Застосовуємо формулу (10.8).
Результат обчислень запишемо у таблицю:
Отримані результати співпадають з результатами по виправленому методу Ейлера.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.172 (0.012 с.) |

 , функцію
, функцію  і її похідні
і її похідні  :
: (10.1)
(10.1) є функцією однієї змінної, то диференційне рівняння називається звичайним.
є функцією однієї змінної, то диференційне рівняння називається звичайним. (10.2)
(10.2) , якщо його можна розв’язати відносно похідної.
, якщо його можна розв’язати відносно похідної. , (10.3)
, (10.3) і задовольняє таким умовам:
і задовольняє таким умовам: ;
; функція повинна дорівнювати заданому
функція повинна дорівнювати заданому  , тобто можна знайти таке значення
, тобто можна знайти таке значення  , при якому функція
, при якому функція  буде задовольняти заданій початковій умові.
буде задовольняти заданій початковій умові. (інтегральні криві).
(інтегральні криві). , значенні
, значенні  . Йому відповідає одна із інтегральних кривих, яка проходить через задану точку початкових умов (
. Йому відповідає одна із інтегральних кривих, яка проходить через задану точку початкових умов ( ).
). .
. в точці
в точці  достатньо даних тільки про попередню точку
достатньо даних тільки про попередню точку  . Ці методи не потребують обчислень похідних від
. Ці методи не потребують обчислень похідних від  - достатньо обчислень самої функції.
- достатньо обчислень самої функції. (10.4)
(10.4) при заданих початкових умовах:
при заданих початкових умовах:  при
при 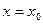 . Ним буде функція
. Ним буде функція  обчислюємо одним із чисельних методів.
обчислюємо одним із чисельних методів. на
на  рівних частин. Їх величина (крок) дорівнює:
рівних частин. Їх величина (крок) дорівнює: . (10.5)
. (10.5) і, відповідно,
і, відповідно, 
 обчислюються за формулою:
обчислюються за формулою: (10.6)
(10.6) (хк, ук) - значення функції (10.4) в точці
(хк, ук) - значення функції (10.4) в точці 
 (10.7)
(10.7)
 (10.8)
(10.8)
 у розкладенні функції
у розкладенні функції  (10.9)
(10.9) на відрізку [ 0;1 ], яке задовольняє початковим умовам:
на відрізку [ 0;1 ], яке задовольняє початковим умовам:  при
при 
 .
. частин точками
частин точками  . Крок
. Крок 
 функції
функції 



 . Точне її значення:
. Точне її значення:  .
. . Збільшення
. Збільшення 
 при
при  складає
складає 




