
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельного інтегрування функцій методом СимпсонаСодержание книги
Поиск на нашем сайте
Мета роботи: Закріплення знань із застосування чисельного інтегрування функцій методом Симпсона, розробка відповідного алгоритму і програми на мові Pascal, застосування її для розв’язання індивідуального завдання. Теоретичні відомості Метод Симпсона - один із поширених методів чисельного інтегрування функцій. Аналогічно методу трапецій, інтегрування проводиться шляхом розбиття загального інтервалу інтегрування [ a,b ] на багато дрібних відрізків. Для обчислення площі над кожним із них, через три послідовні ординати розбиття проводиться квадратична парабола. Тобто крива f(x) на малому відрізку замінюється параболою L(x), яка проходить через 3 точки Mi(xi, yi); Mi+1 (xi+1, yi+1); Mi+2(xi+2, yi+2):
Припускаємо, що кількість відрізків n=2m - парне число. Відомі yi=f(xi), i=0,1,2…,n – значення підінтегральної функції у рівновіддалених точках: x0=a; x1=a+h; x2=a+2h;... xi=a+ih; …, xn=b,
де h - крок інтегрування:
Тоді загальну формулу Сімпсона можна записати:
Формула Симпсона дає похибку, яка дорівнює сумі площ заштрихованих фігур (з урахуванням знаків). При інтегруванні багаточленів до третього порядку включно, формула Симпсона дає точне значення інтеграла.
Приклад обчислення інтегралу за формулою Симпсона Обчислюємо значення інтеграла
Отримане значення дорівнює точному значенню інтеграла. Алгоритмічна та програмна реалізація формули Сімпсона
Var A,B,H,I,x,y:real; I,n:integer; Begin <введення вихідних даних> H:=(B-A)/n; I:=sqrt(1+2*A) + sqrt(1+2*B); X:=A; For i:=1 to n/2 do Begin X:=x+H; Y:=sqrt(1+2*x); I:=I+4*y; X:=x+H; Y:=sqrt(1+2*x); I:=I+2*x;
I:=I*H/3; <виведення результатів> Примітки: 1. В програмі реалізоване обчислення інтегралу, що розглянутий у прикладі; 2. Якщо функція f(x) задана таблично, то треба організувати введення масиву з ординатами точок.
Порядок виконання роботи
Виконати завдання Заняття №7, застосувавши для чисельного інтегрування заданої функції формулу Сімпсона. Заняття № 9 Розробка програми чисельного диференціювання функцій Мета роботи: Закріплення знань із застосування методів чисельного диференціювання функцій і використання для цього інтерполяційного полінома Лагранжа, розробка відповідного алгоритму і програми на мові Pascal, застосування її для диференціювання заданої функції.
Теоретичні відомості Чисельне (наближене) диференціювання функцій використовують у випадку, коли функція
Інтерполююча функція Для обчислення значень інтерполюючого поліному поліном подається у вигляді
Обчислення починаються із внутрішніх дужок:
Послідовно обчислюючи Приклад обчислення похідних функцій Виконати чисельне диференціювання функції У Завданні № 6 розглянутий приклад, в якому для цієї функції сформований інтерполюючий поліном Лагранжа при
Визначимо першу і другу похідні:
Обчислимо наближені значення першої похідної у вузлах інтерполяції і порівняємо їх з точними значеннями:
Обчислюємо значення другої похідної у вузлах інтерполяції:
Обчислимо точні і наближені значення похідних
Наближене диференціювання функцій дає результат з більшою похибкою, ніж інтерполяція. Алгоритмічна та програмна реалізація чисельного Диференціювання функцій Функція
Обчислити наближені значення похідних функції у точці
A1,A2: array [0...10] of real; n1, n2: integer; begin <введення вихідних даних> P1:=0; for i:=n1 downto 0 do P1:= A1[i]+XP*P1; P2:=0; for i:=n2 downto o do P2:=A2[i]+XP*P2; <виведення результатів> …
1. Масиви А1 і А2 містять коефіцієнти поліномів n1, n2 - порядок цих поліномів; 2. Для обчислення значень поліномів при 3. Результати обчислень - значення похідних при Порядок виконання роботи 1. Ознайомитись з теоретичним матеріалом з питань чисельного диференціювання функцій, використанням для цього інтерполюючи поліномів Ньютона, Лагранжа; 2. Для виконання завдання використати інтерполюючий поліном Лагранжа 3. Визначити першу і другу похідні від цього поліному 4. Обчислити точні і наближені значення похідних при трьох вибраних значеннях 5. Скласти докладний алгоритм обчислення наближених значень похідних. Для обчислення значень поліномів використати правило Горнера; 6. Скласти і відлагодити програму на мові програмування Pascal, яка реалізує введення вихідних даних, обчислення наближених значень похідних при довільному значенні Основні фрагменти програми реалізувати як процедури і функції; 7. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 8. З використанням розробленої програми повторити п.4, порівняти результати. 9. Обчислити точні значення похідних і їх наближені значення (з використанням розробленої програми) у десяти точках Результати оформити у вигляді таблиці; 10. Сформулювати висновки по роботі.
Результати виконання кожного пункту завдання докладно описати у звіті по роботі. Використання без змін в розробленій програмі фрагменту, наведеного у п. 9.2., заслуговує на мінімальну оцінку. Для отримання підвищеної оцінки необхідно розробити власний варіант програми.
Заняття № 10 Розробка програми
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.1.159 (0.009 с.) |












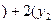


 .
. , який розглянуто у Завданні № 7, при n=2m =10:
, який розглянуто у Завданні № 7, при n=2m =10: 

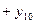 )
) 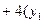







 End;
End;
 задана таблично (тобто у вигляді масива точок з координатами
задана таблично (тобто у вигляді масива точок з координатами  ), або якщо аналітичний вираз функції достатньо складний і безпосереднє диференціювання її викликає труднощі. При цьому функцію
), або якщо аналітичний вираз функції достатньо складний і безпосереднє диференціювання її викликає труднощі. При цьому функцію  на інтервалі
на інтервалі  замінюють інтерполюючою функцією
замінюють інтерполюючою функцією  (зазвичай поліномом) і припускають, що:
(зазвичай поліномом) і припускають, що:
 при заданому
при заданому  можна застосувати правило Горнера:
можна застосувати правило Горнера: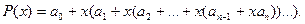

 отримаємо значення поліному
отримаємо значення поліному 
 , заданої таблично.
, заданої таблично. :
:

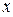
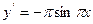




 при значеннях
при значеннях  , що не співпадають з вузлами інтерполяції (
, що не співпадають з вузлами інтерполяції ( ):
):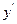

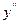
 і визначені похідні від нього
і визначені похідні від нього  .
. .
. Var P1,P2,XP: real;
Var P1,P2,XP: real; Примітки:
Примітки: ;
; реалізується формула Горнера;
реалізується формула Горнера; містяться у змінних P1 i P2.
містяться у змінних P1 i P2. , який сформований відповідно до індивідуального завдання на Занятті № 6;
, який сформований відповідно до індивідуального завдання на Занятті № 6; ;
; , які розташовані відповідно, на початку, в середині і в кінці інтервалу
, які розташовані відповідно, на початку, в середині і в кінці інтервалу  ;
; , виведення результатів у зручній формі на екран і в файл.
, виведення результатів у зручній формі на екран і в файл. . Визначити похибку
. Визначити похибку  .
.


