
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна та програмна реалізація методів Ейлера для розв’язання ЗДРСодержание книги
Поиск на нашем сайте
Алгоритм реалізує розв’язання ЗДР трьома розглянутими модифікаціями метода Ейлера - в залежності від значення Значення функції 1. Метод Ейлера; 2. Виправлений метод Ейлера; 3. Модифікований метод Ейлера. В програмі реалізовано розв’язання диференційного рівняння, що розглянуте у прикладі. Program EILER; Var x0, y0, b, F,F1, h,w:real; n, i, k:integer; x: array [0..100] of real; E:array [1..3,0..100] of real; Label M; Begin <введення вихідних даних> h:=(b-x0)/n; x[0]:=x0; for i:= 1 to 3 do E[i,0]:=y0; for k:=1 to n do begin x[k]:=x[k-1]+h; w:=0; for i:=1 to 3 do begin F:=x[k-1]+E[і,k-1]; If w=0 then goto M; F1:=(x[k-1]+h/(2*w))+(E[i,k-1]+h*F/(2*w)); M: E[i,k]:=E[i,k-1]+h*((1-w)*F+w*F1); w:=w+0.5; end; end; <виведення результатів> end.
Порядок виконання роботи 1. Вибрати індивідуальне завдання. Номер варіанту у таблиці 10.1. відповідає номеру студента у списку групи; 2. Ознайомитись із теоретичним матеріалом з питань чисельного розв’язання диференційних рівнянь. 3. Записати задане рівняння у формі (10.4); 4. Обчислити точні значення розв’язку заданого ЗДР 5. Обчислити наближені значення розв’язку заданого диференційного рівняння на відрізку Визначити похибки. Результати п. 4 і п. 5 оформити у вигляді таблиці; 6. Скласти докладний алгоритм чисельного розв’язання ЗДР методами Ейлера; 7. Скласти і відлагодити програму на мові Pascal, яка реалізує: · введення даних; · обчислення точних значень розв’язку заданого ЗДР у визначених точках; · наближене розв’язання ЗДР методами Ейлера; · обчислення похибок наближеного розв’язання; · виведення результатів у файл; · подання результатів у вигляді графіків. Основні фрагменти програми оформити як процедури і функції; 8. Описати розроблений алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 9. З використанням розробленої програми розв’язати (точно і наближено) задане диференційне рівняння при 10. Розв’язати задане диференційне рівняння при
· точний розв’язок · розв’язок методом Ейлера; · розв’язок модифікованим методом Ейлера. Графіки оформити з використанням додаткових ефектів; 11. Сформулювати висновки по роботі. Результати виконання кожного пункту завдання докладно описати у звіті по роботі. Використання без змін в розробленій програмі фрагменту, наведеного у п. 10.2., заслуговує на мінімальну оцінку. Для отримання підвищеної оцінки необхідно розробити власний варіант програми.
Таблиця 10.1. Варіанти завдань до занять №10 та №11
Заняття № 11 Розробка програми Чисельного розв’язання ЗДР методом Рунге-Кутта четвертого порядку Мета роботи: Закріплення знань із застосування методів Рунге-Кутта для чисельного розв’язання звичайних диференційних рівнянь, розробка відповідного алгоритму та програми на мові Pascal, застосування її для розв’язання заданого диференційного рівняння. Теоретичні відомості Загальні положення і постановка задачі розв’язання звичайних диференційних рівнянь (ЗДР) першого порядку чисельними методами описані у попередній роботі. Метод Рунге-Кутта 4-го порядку є найбільш поширеним методом розв’язання ЗДР і систем рівнянь. Його перевага - висока точність результату. Відповідно до методу, наближені значення функції
Де Крок інтегрування
стає великим (більше кількох сотих), то крок інтегрування необхідно зменшити. Приклад розв’язання диференційного рівняння методом Рунге-Кутта четвертого порядка Визначити наближене розв’язання диференційного рівняння 1-го порядку Ділимо відрізок Точним розв’язком рівняння є функція
Для наближеного розв’язання рівняння (обчислення значень функції
Обчислюємо значення функції:
Аналогічно обчислюємо значення функції
Отримані результати співпадають з точним розв’язком диференційного рівняння в точках розбиття
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.148.189 (0.008 с.) |

 .
. ;
; 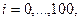 що обчислені по кожній із формул, розміщуються у двомірному масиві
що обчислені по кожній із формул, розміщуються у двомірному масиві 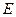 розмірністю
розмірністю  . Кожний із рядків масиву відповідає одному із методів:
. Кожний із рядків масиву відповідає одному із методів:

 в точках відрізку
в точках відрізку  при
при  ;
; і побудувати у спільній системі координат графіки інтегральних кривих:
і побудувати у спільній системі координат графіки інтегральних кривих:




 =
= 


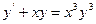








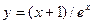




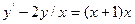

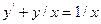





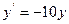







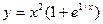
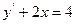





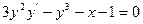














 обчислюються за формулою:
обчислюються за формулою: (11.1)
(11.1)
 обчислюється за формулою (10.5). Його правильний вибір дозволяє підвищити точність результату. Існує грубе оціночне правило: якщо співвідношення
обчислюється за формулою (10.5). Його правильний вибір дозволяє підвищити точність результату. Існує грубе оціночне правило: якщо співвідношення (11.2)
(11.2) на відрізку
на відрізку  , яке задовільняє початковим умовам:
, яке задовільняє початковим умовам:  при
при  .
. . Обчислюємо крок
. Обчислюємо крок 
 . Її значення в точках розбиття
. Її значення в точках розбиття 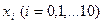 :
: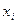

 в точках розбиття) методом Рунге-Кутта 4-го порядку, застосовуємо формулу (11.1). Для заданого рівняння вона набуває вигляду:
в точках розбиття) методом Рунге-Кутта 4-го порядку, застосовуємо формулу (11.1). Для заданого рівняння вона набуває вигляду:



 в інших точках і результати записуємо в таблицю:
в інших точках і результати записуємо в таблицю:


