
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна і програмна реалізація метода подвійної факторизаціїСодержание книги
Поиск на нашем сайте
Розв’язуємо систему лінійних рівнянь за формулою (3.1) з використанням оберненої матриці коефіцієнтів а) факторизація матриці коефіцієнтів А. результатом перетворень є факторизована матриця б) розв’язання системи лінійних рівнянь і обчислення значень невідомих Х. Можливі два варіанти реалізації. Перший передбачає обчислення оберненої матриці При виконанні лабораторної роботи студенти реалізують другий варіант. Він дозволяє формувати ефективний алгоритм і економити оперативну пам’ять ПК, оскільки не потребує використання додаткових масивів для зберігання проміжних результатів обчислень. Процес перемноження факторних матриць при розв’язанні системи рівнянь можна поділити на 2 етапи:
а)
б)
Перемноження матриці на вектор виконується за відомою схемою:
Тобто кожний елемент вектора Після реалізації цих обчислень в масиві В будуть знаходитись значення Х, які є розв’язком системи рівнянь. Отриманий результат треба вивести на екран і у файл. Для перевірки правильності розв’язання системи необхідно підставити обчислені значення у вихідну систему і виконати перемноження.
Алгоритм і програма подвійної факторизації матриці використовують такі масиви і змінні: а - елементи матриці А ( двомірний масив розмірністю n - кількість рядків і стовпців матриці;
k - номер кроку факторизації (k=1,…,n); i, j - номер рядка і номер стовпця матриці. На вході програми - двомірний масив - вихідна матриця коефіцієнтів А, на виході – факторизована матриця
1. Опорний елемент відповідно до (3.3); 2. Елемент матриці 3. Інші елементи рядка і відповідно до (3.5); 4. Елемент матриці Програмна реалізація: … for k:=1 to n do Begin a[k,k]:=1/a[k,k]; for i:=k+1 to n do Begin a[i,k]:= - a[i,k]*a[k,k]; for j:=k+1 to n do a[i,j]:=a[i,j]+a[i,k]*a[k,j]; End; For j:=k+1 to n do a[k,j]:= - a[k,j]*a[k,k]; end; …
Алгоритм і програма розв’язання СЛАР використовують такі змінні і масиви: А - елементи факторизованої матриці в - елементи допоміжного масиву В ( одномірний масив ); n - кількість рядків і стовпців у масивах k - номер кроку факторизації.
1. Перемноження лівих факторних матриць На вході фрагмента програми - факторизована матриця відповідають факторним матрицям лівих факторних матриць
Алгоритм: Програмна реалізація:
For k:=1 to n do Begin for j:=n downto k+1 do B[j]:=B[j]+A[j,k]*B[k]; B[k]:=A[k,k]*B[k]; End; …
2. Перемноження правих факторних матриць
Алгоритм:
Програмна реалізація: … for k:=n-1 downto 1 do Begin For j:=n downto k+1 do B[k]:=B[k]+a[k,j]*B[j]; End; …
Порядок виконання роботи Виконати завдання Заняття № 2 (розділ 2.3), застосовувавши для розв’язання заданної СЛАР метод подвійної факторизації.
Заняття № 4 Розробка програми Розв’язання системи нелінійних алгебраїчних рівнянь (СНАР) Методом Зейделя Мета роботи: Закріплення знань із застосування ітераційних методів для чисельного розв’язання СНАР, вивчення алгоритмів метода Зейделя і простої ітерації, розробка відповідної комп’ютерної програми на мові Pascal і застосування її для розв’язання заданої системи рівнянь.
Теоретичні відомості Методи простої ітерації і Зейделя для розв’язання СНАР
Ці методи належать до групи ітераційних методів, що застосовуються для розв’язання систем нелінійних алгебраїчних рівнянь. Дозволяють отримати значення невідомих величин із заданою точністю, як результат виконання послідовності ітерацій. У загальному вигляді нелінійну систему рівнянь можна записати:
Для її розв’язання методами простої ітерації і Зейделя, систему необхідно перетворити: розв’язати кожне і - те рівняння системи відносно відповідної невідомої величини Перетворена система набуває загального вигляду:
При підстановці в праву частину цієї системи чергового наближення невідомих величин При цьому ітераційна форма запису системи має вигляд:
Підставивши в (4.3) нове наближення невідомих і виконавши обчислення, знаходимо нові значення невідомих і т.д. Це відповідає послідовності розрахунків за методом простої ітерації. Більш ефективним по показниках збіжності є модифікація методу простої ітерації - метод Зейделя. Відмінність методу Зейделя полягає в тому, що для визначення чергового (к+1)- го наближення і - го невідомого Система рівнянь (4.3) при розв’язанні її методом Зейделя набуває вигляду:
Ітерації повторюються доти, поки не стане виконуватись умова (1.6) для всіх невідомих, або умова (1.7) - для всіх рівнянь системи.
Послідовність дій при розв’язанні СНАР методом Зейделя: 1. Перетворення вихідної системи у форму (4.2) і запис її в ітераційній формі (4.4). 2. Визначення початкового наближення невідомих У випадку системи двох рівнянь з двома невідомими, початкові наближення коренів і їх кількість можна знайти, виконавши побудову графіків для кожного рівняння системи на площині
Координати 3. Обчислення наступного наближення невідомих. Підставляємо вибрані наближення коренів (на 1-й ітерації – це початкові наближення) у перше рівняння системи (4.4) і обчислюємо 4. Контроль завершення ітераційного процесу за умовами досягнення заданої точності Якщо точність досягнута, то обчислені на цій ітерації наближення коренів
Приклад розв’язання СНАР методом Зейделя Знайти корені системи 3-х нелінійних рівнянь з трьома невідомими. Точність
Система рівнянь у формі (4.1):
Перетворюємо систему у форму (4.2):
Записуємо систему в ітераційній формі по методу Зейделя:
Вибираємо початкові наближення невідомих Ітерація 1. Визначаємо перші наближення невідомих:
Нев’язки рівнянь при цих наближеннях:
Нев’язки рівнянь
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.102 (0.01 с.) |

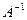 . Для обернення матриці застосовуємо метод подвійної факторизації. Виконується два етапи обчислень:
. Для обернення матриці застосовуємо метод подвійної факторизації. Виконується два етапи обчислень: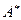 , що розташована на полі вихідної матриці (тобто в тому ж масиві). Його елементи є елементами факторних матриць
, що розташована на полі вихідної матриці (тобто в тому ж масиві). Його елементи є елементами факторних матриць 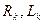 . Можливий варіант алгоритму і програмної реалізації подвійної факторизації описано нижче.
. Можливий варіант алгоритму і програмної реалізації подвійної факторизації описано нижче.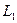 до
до 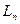 і від
і від 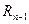 до
до  ). Результат кожного множення розміщується в поле масиву В.
). Результат кожного множення розміщується в поле масиву В.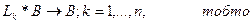


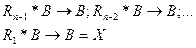

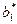


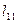
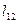

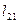
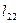
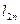
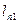
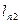
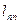
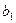

 …
…
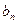

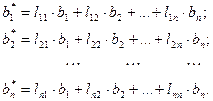
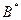 обчислюється як сума добутків усіх елементів відповідного рядка матриці на всі елементи вектора В.
обчислюється як сума добутків усіх елементів відповідного рядка матриці на всі елементи вектора В.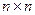 );
);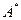 .
.
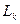 відповідно (3.3);
відповідно (3.3);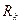 відповідно до (3.4);
відповідно до (3.4);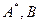 ;
;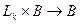 (k=1,…,n).
(k=1,…,n).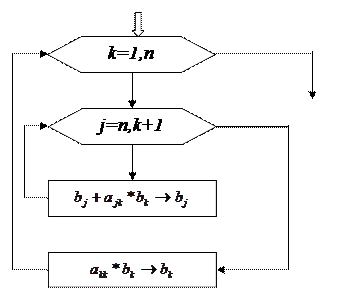 …
…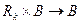 (k=n-1,…,1). На вході фрагмента програми - факторизована матриця
(k=n-1,…,1). На вході фрагмента програми - факторизована матриця 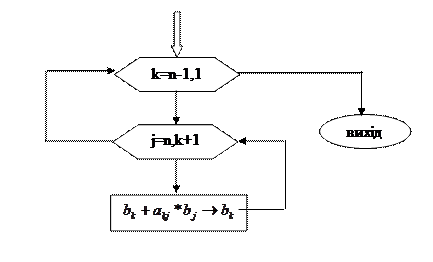
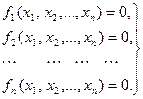 (4.1)
(4.1)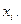
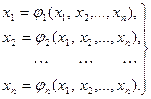 (4.2)
(4.2)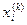 і виконанні необхідних обчислень, можна отримати наступне наближення невідомих
і виконанні необхідних обчислень, можна отримати наступне наближення невідомих 
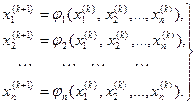 (4.3)
(4.3)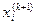 використовуються ( к+1 ) -і наближення невідомих
використовуються ( к+1 ) -і наближення невідомих 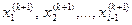 , що обчислені на цій же (к+1 ) -й ітерації, а також к -ті наближення невідомих
, що обчислені на цій же (к+1 ) -й ітерації, а також к -ті наближення невідомих 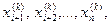 обчислених на попередній к -ій ітерації.
обчислених на попередній к -ій ітерації.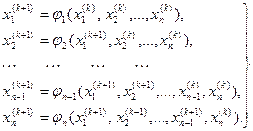 (4.4)
(4.4)
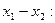
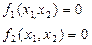 :
: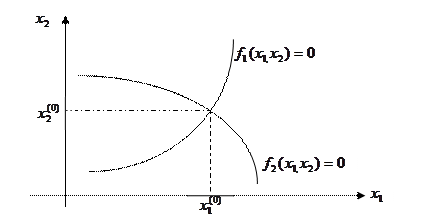
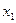 і
і 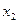 точок перетину графіків відповідають значенням коренів системи рівнянь і можуть бути прийняті як їх початкові наближення.
точок перетину графіків відповідають значенням коренів системи рівнянь і можуть бути прийняті як їх початкові наближення.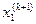 . Із другого рівняння отримаємо
. Із другого рівняння отримаємо  , використовуючи нове значення
, використовуючи нове значення 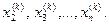 Із наступних рівнянь отримаємо (к+1 )- і наближення всіх інших невідомих.
Із наступних рівнянь отримаємо (к+1 )- і наближення всіх інших невідомих.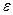 .
.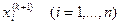 є розв’язком системи рівнянь із заданою точністю
є розв’язком системи рівнянь із заданою точністю 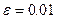 .
.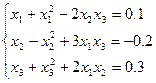
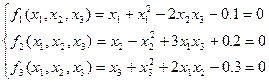
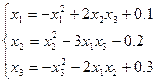

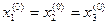 =0.
=0.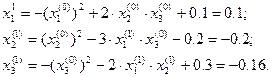
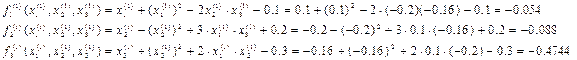
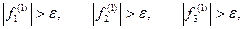 тому виконуємо наступну ітерацію. Обчислення виконуються до досягнення заданої точності.
тому виконуємо наступну ітерацію. Обчислення виконуються до досягнення заданої точності.


