Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язання слар методом подвійної факторизаціїСодержание книги
Поиск на нашем сайте
Мета роботи: Закріплення знань із застосування метода подвійної факторизації для розв’язання СЛАР, вивчення алгоритму метода, розробка відповідної комп’ютерної програми на мові Pascal і використання її для розв’язання заданої системи рівнянь
3.1. Теоретичні відомості
Метод подвійної факторизації розв’язання Метод подвійної факторизації є прямим методом розв’язання СЛАР. Використовує обернену матрицю коефіцієнтів. Для системи лінійних рівнянь (2.2) це розв’язання має вигляд:
Метод дозволяє зменшити обчислювальні проблеми, що виникають при оберненні матриці коефіцієнтів, яка в практичних задачах може мати велику розмірність і малу заповненість. Метод включає два основних етапи: 1. Обернення матриці коефіцієнтів методом подвійної факторизації; 2. розв’язання системи рівнянь перемноженням оберненої матриці А-1 на вектор вільних членів системи В відповідно до (3.1). Подвійна факторизація (елімінативна форма оберненої матриці) - це подання оберненої матриці як добутку послідовності елементарних верхніх та нижніх трикутних матриць, в яких не дорівнює нулю тільки один стовпець чи рядок:
де k - номер кроку перетворення матриці А (крок факторизації); Rk, Lk - верхні та нижні трикутні матриці на k -му кроці перетворення (факторні матриці).
Верхня трикутна матриця (права факторна матриця) має таку структуру:
Це матриця з одиничною діагоналлю та відмінними від нуля над- діагональними елементами в k -му рядку. Усі інші елементи матриці дорівнюють нулю.
Нижня трикутна матриця (ліва факторна матриця) має структуру:
Її діагональні елементи дорівнюють одиниці, за винятком k - гостовпця. У ньому елементи, що розташовані на діагоналі і нижче її, відмінні від нуля. Усі інші елементи матриці дорівнюють нулю.
Елементи факторних матриць Матриця
Матриця де
k - номер кроку факторизації k=1, …, n; J - елементи матриці коефіцієнтів на k - му кроці факторизації.
На кожному кроці факторизації виконується перерахунок усіх елементів не перетвореної раніше частини матриці (Рис. 3.1) за формулою:
 j i, j=k+1,…,n j i, j=k+1,…,n
В результаті виконання n кроків перетворення отримуємо (n-1) праву факторну матрицю R і n лівих факторних матриць L (всього 2n-1 елементарних трикутних матриць). Їх елементи розташовані на полі вихідної матриці А і утворюють факторизовану матрицю
… Загальний алгоритм подвійної факторизації матриці передбачає виконання таких кроків: 1) визначення номера чергового кроку факторизації k (k=1, …, n); 2) вибір чергового опорного елемента 3) обчислення елементів k - ої факторної матриці 4) обчислення інших елементів матриці А, що не входили в опорні рядок і стовпець на цьому і попередніх кроках перетворення. Використовується формула (3.5); 5) обчислення елементів k -ої факторної матриці 6) якщо таким чином виконано n кроків перетворення і сформовано факторизовану матрицю що містить елементи (n-1) матриці R і n матриць L, то подвійна факторизація завершується. В іншому випадку - повернення до пункту 1) і виконання наступного кроку перетворення.
Після завершення факторизації з факторизованої матриці можна виділити факторні матриці R, L і визначити обернену матрицю
Приклад розв’язання СЛАР методом подвійної факторизації
Розв’яжемо СЛАР (2.16) методом подвійної факторизації. Матриця коефіцієнтів системи має вигляд:
А=
Виконуємо факторизацію матриці відповідно до алгоритму. Необхідно виконати 3 кроки факторизації (n=3). Перший крок факторизації (к=1). Опорний елемент к=1; і=2,3; j=2,3.
Переобчислюємо елементи матриці,що не увійшли у опорний рядок і стовпець, за формулою (3.5):
Визначаємо елементи правої факторної матриці R, за формулою (3.4):
В результаті виконання 1-го кроку факторизації, визначені елементи факторних матриць
Другий крок факторизації (к=2). Опорний елемент k=2, i=3; j=3.
В результаті другого кроку факторизаціїї визначені елементи факторних матриць
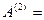
Третій крок факторизації (к=3). Опорний елемент
В результаті останнього, третього, кроку визначено елемент вакторної матриці
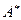 = =
Її елементами є елементи факторних матриць
Розв’язуємо систему рівнянь відповідно до алгоритму. Розв’язок визначаємо в результаті послідовного перемноження матриць

Таким чином, розв’язком системи рівнянь є вектор:
Для перевірки правильності розв’язання системи необхідно елементи вектора Х підставити у вихідну систему рівнянь. Рівняння системи перетворюється на тотожності, тобто вона розв’язана вірно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.241.214 (0.008 с.) |

 (3.1)
(3.1) , (3.2)
, (3.2)
 ak,n
ak,n




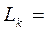

 на k - мукроці факторизації обчислюються за формулами:
на k - мукроці факторизації обчислюються за формулами: :
: 
 (3.3)
(3.3)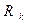 :
: 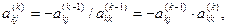 (3.4)
(3.4) - номери рядка та стовпця матриці коефіцієнтів
- номери рядка та стовпця матриці коефіцієнтів
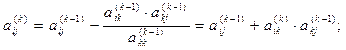 (3.5)
(3.5)






 R2
….……/
R2
….……/
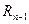

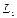
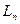


 . Це діагональний елемент, що розташований на перетині k - го рядка і k - го стовпця (опорні рядок та стовпець);
. Це діагональний елемент, що розташований на перетині k - го рядка і k - го стовпця (опорні рядок та стовпець);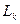 за формулами (3.3);
за формулами (3.3); ;
;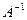 відповідно до (3.2).
відповідно до (3.2). . Визначаємо елементи лівої факторної матриці
. Визначаємо елементи лівої факторної матриці 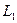 за формулами (3.3).
за формулами (3.3).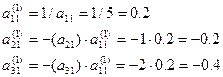


 . Вони розташовані на полі вихідної матриці. Перетворена матриця на цьому етапі має вигляд:
. Вони розташовані на полі вихідної матриці. Перетворена матриця на цьому етапі має вигляд:
 =
= .
.
 і
і  . Матриця набуває вигляду:
. Матриця набуває вигляду: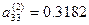 .
. .
. . Отримано факторизовану матрицю, яка має остаточний вигляд:
. Отримано факторизовану матрицю, яка має остаточний вигляд:


 на вектор вільних членів В (відповідно до формул (3.2) і (3.1)):
на вектор вільних членів В (відповідно до формул (3.2) і (3.1)):