
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна та програмна реалізація метода НьютонаСодержание книги
Поиск на нашем сайте
Var X0, E, XK, XK1, FK, FK1: real; k: integer; label M,M1; Begin <введення вихідних даних> K:=0; XK:=X0; M1: FK:=XK*XK*XK-5*XK-10; FK1:=3*XK*XK-5; XK1:=XK-FK/FK1; FK:=XK1*XK1*XK1-5*XK1-10; If abs(FK)< =E then goto M; XK:=XK1; K:=K+1; goto M1; M: <виведення результатів> … Примітки: 1. Фрагмент програми реалізує розв’язання рівняння, яке розглянуто у прикладі; 2. Вихідними даними є початкове наближення кореня 3. Результати – наближення кореня із заданою точністю ХК1, точність Е і кількість ітерацій k.
Порядок виконання роботи 1. Вибрати індивідуальне завдання. Номер варіанту в Таблиці 1.1. відповідає номеру студента у списку групи; 2. Ознайомитись із теоретичним матеріалом по чисельним методам розв’язання рівнянь; 3. Виконати «ручне» розв’язання заданого рівняння методом Ньютона (до 5 ітерацій); 4. Скласти докладний алгоритм розв’язання рівняння методом Ньютона; 5. Скласти і відлагодити програму на мові Pascal, яка реалізує введення вихідних даних, розв’язання заданого рівняння, виведення результатів у зручній формі на екран і в файл. Основні фрагменти програми оформити як процедури і функції. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 6. Розв’язати задане рівняння за допомогою розробленої програми з точністю ε =0.01. Порівняти отримані результати із результатами «ручних» розрахунків. Побудувати графік збіжності ітераційного процесу 7. Обчислити корінь рівняння при 5 різних значеннях точності 8. Повторити п.7 з використанням умови (1.6), внісши відповідні зміни у програму. Результати п.6 і п.7 оформити у вигляді таблиці; 9. Обчислити інші дійсні корені рівняння; 10. Підготувати висновки по роботі.
Результати виконання кожного пункту докладно описати у звіті по роботі. Для отримання підвищеної оцінки необхідно на основі наведеного фрагменту програми розробити власну програму.
Таблиця 1.1. Варіанти завдань до Заняття № 1
Заняття № 2 Розробка програми розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) методом Гауса Мета роботи: Закріплення знань із застосування метода Гауса для розв’язання СЛАР, вивчення алгоритму метода, розробка відповідної комп’ютерної програми на мові Pascal і застосування її для розв’язання заданої системи рівнянь
A. Теоретичні відомості Метод Гауса для розв’язання СЛАР
Система n лінійних рівнянь з n невідомими у загальному вигляді може бути записана:
де системи;
У матричній формі ця система рівнянь має вигляд:
або де А - квадратна матриця коефіцієнтів системи розмірністю x - вектор невідомих; В - вектор вільних членів. Розв’язати систему (2.1) - означає обчислити такі значення елементів вектора невідомих Для цього можна застосувати як прямі, так і ітераційні методи. Найбільш поширеним прямим способом розв’язання систем лінійних рівнянь є алгоритм послідовного виключення невідомих, що має назву метод Гауса. Існують різні алгоритми його реалізації. Один із них - метод Гауса із зворотнім ходом для розв’язання СЛАР розглядається у цій роботі. Метод Гауса із зворотнім ходом передбачає виконання двох етапів: прямий і зворотній хід методу. Прямий хід - послідовність однотипних кроків виключення невідомих із системи рівнянь. В результаті його виконання вихідна система (2.1) або (2.2) з прямокутною матрицею коефіцієнтів перетворюється на еквівалентну систему рівнянь з верхньою трикутною матрицею коефіцієнтів. На зворотному ході обчислюються значення невідомих, починаючи з останнього (від
Прямий хід: Перший крок виключення невідомих. Виключаємо невідому
Тобто він повинен бути відмінним від нуля і серед елементів першого стовпця матриці коефіцієнтів в (2.2) найбільшим за абсолютною величиною. В іншому разі переставимо рівняння в системі так, щоб ці умови виконувались.
Ділимо перше рівняння системи (2.1) на опорний елемент
Для виключення складових з невідомим
де
номер рівняння в системі, і = 2, …, n; j - номер елемента в рівняннях, j = 1, …, n. На другому кроці виключення невідомих необхідно виключити
Виключаємо доданки з невідомим
де
Наступні кроки виключення невідомих виконуються аналогічно. На k -му кроці коефіцієнти і вільні члени системи рівнянь обчислюються за такими формулами:
де к = 1, …, n-1 – номер кроку виключення невідомих, що збігається з номером рівняння системи, в якому розташований опорний елемент; і = k+1, …, n - номер рівняння, з якого виключається невідома; j = k, …, n - номер елемента в рівнянні.
Опорний елемент
Після виконання останнього ( n-1 ) -го кроку виключення невідомих вихідна система рівнянь перетворюється на еквівалентну систему з верхньою трикутною матрицеюкоефіцієнтів:
Зворотній хід: Обчислюємо значення всіх невідомих, починаючи з
Підставляємо його в передостаннє рівняння і обчислюємо
Послідовно визначаємо
Для перевірки правильності розв’язання системи рівнянь, необхідно обчислені значення невідомих
Приклад розв’язання СЛАР методом Гауса Обчислити корені системи 3-х лінійних рівнянь з трьома невідомими
Прямий хід. Необхідно виконати 2 кроки виключення невідомих. На першому кроці (к=1)виключаємо невідому
і виконуємо виключення. Для цього робимо перетворення відповідно до (2.6) при і=2,3; j=1,2,3: і=2,
Таким чином, в результаті перетворень, друге рівняння (i=2) набуває вигляду:
і=3,
Третє рівняння (і=3) набуває вигляду: 0+0.6 Отримуємо еквівалентну систему рівнянь:
На другому кроці (к=2) виключаємо невідому
і виконуємо виключення. При і=3, j=2,3 відповідно до (2.9) отримуємо:
і=3
Третє рівняння системи (2.17) набуває вигляду: 0+0.3182 Отримуємо еквівалентну систему рівнянь з трикутною матрицею коефіцієнтів:
Зворотній хід. Із останнього рівняння системи (2.18) знаходимо:
Підставляємо обчислене значення
Із першого рівняння системи знаходимо:
Таким чином, розв’язком системи є вектор
Для перевірки правильності розв’язання системи рівнянь підставляємо елементи вектора Х у вихідну систему (2.16). Рівняння системи перетворюється на тотожності, що підтверджує правильність її розв’язання.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.138 (0.008 с.) |


 і точність Е;
і точність Е;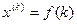 ;
;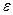 (
(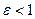 ). Контроль завершення ітераційного процесу – за умовою (1.7);
). Контроль завершення ітераційного процесу – за умовою (1.7);
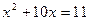
















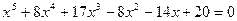













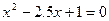




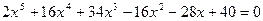
 (2.1)
(2.1) -невідомі величини, які необхідно визначити при розв’язанні
-невідомі величини, які необхідно визначити при розв’язанні - коефіцієнти при невідомих;
- коефіцієнти при невідомих; - вільні члени рівнянь системи.
- вільні члени рівнянь системи. (2.2)
(2.2)

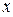 , за яких кожне рівняння системи перетворюється на тотожність.
, за яких кожне рівняння системи перетворюється на тотожність. до
до 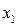 ). Розглянемо докладно можливий варіант перетворень.
). Розглянемо докладно можливий варіант перетворень. із рівнянь системи (2.1), починаючи з другого. Виберемо на діагоналі опорний елемент a
із рівнянь системи (2.1), починаючи з другого. Виберемо на діагоналі опорний елемент a  . При цьому необхідно, щоб виконувались умови:
. При цьому необхідно, щоб виконувались умови: і
і  i=2,…n. (2.3)
i=2,…n. (2.3) ;
;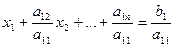 (2.4)
(2.4) із решти рівнянь необхідно рівняння (2.4) по черзі домножати на коефіцієнт
із решти рівнянь необхідно рівняння (2.4) по черзі домножати на коефіцієнт  і результат віднімати від відповідних рівнянь вихідної системи (2.1). В результаті отримаємо еквівалентну систему:
і результат віднімати від відповідних рівнянь вихідної системи (2.1). В результаті отримаємо еквівалентну систему: (2.5)
(2.5) (2.6)
(2.6)
 з рівнянь системи (2.5), починаючи з третього. Вибираємо опорний елемент
з рівнянь системи (2.5), починаючи з третього. Вибираємо опорний елемент  згідно з умовами, подібними до (2.3), тобто
згідно з умовами, подібними до (2.3), тобто  Якщо вони не виконуються, переставимо відповідним чином рівняння 2,3,…, цієї системи. Ділимо друге рівняння системи (2.5) на опорний елемент
Якщо вони не виконуються, переставимо відповідним чином рівняння 2,3,…, цієї системи. Ділимо друге рівняння системи (2.5) на опорний елемент 
 . (2.7)
. (2.7) із рівнянь 3,4,…,n системи (2.5). Для цього рівняння (2.7) по черзі домножаємо на
із рівнянь 3,4,…,n системи (2.5). Для цього рівняння (2.7) по черзі домножаємо на 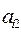 (і = 3, …, n) і результат віднімаємо від відповідних рівнянь. Отримуємо еквівалентну систему:
(і = 3, …, n) і результат віднімаємо від відповідних рівнянь. Отримуємо еквівалентну систему: (2.8)
(2.8)
 (2.9)
(2.9)

 , (2.10)
, (2.10) вибирається в стовпці відповідно до умов:
вибирається в стовпці відповідно до умов: (2.11)
(2.11) (2.12)
(2.12)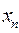 . Із останнього рівняння системи (2.12) отримаємо:
. Із останнього рівняння системи (2.12) отримаємо: (2.13)
(2.13)
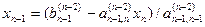 (2.14)
(2.14) із решти рівнянь. Останнім обчислюється
із решти рівнянь. Останнім обчислюється  із першого рівняння при підстановці в нього всіх значень
із першого рівняння при підстановці в нього всіх значень  . В загальній формі ці обчислення можна описати:
. В загальній формі ці обчислення можна описати: (2.15)
(2.15) підставити у вихідну систему (2.1). Усі рівняння повинні перетворитись при цьому на тотожності.
підставити у вихідну систему (2.1). Усі рівняння повинні перетворитись при цьому на тотожності.
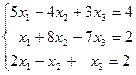 (2.16)
(2.16) із другого і третього рівнянь системи (2.16). Опорний елемент
із другого і третього рівнянь системи (2.16). Опорний елемент  =5. Ділимо на нього перше рівняння системи (2.16):
=5. Ділимо на нього перше рівняння системи (2.16):
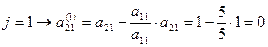




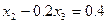
 (2.17)
(2.17) із третього рівняння системи (2.17). Опорний елемент
із третього рівняння системи (2.17). Опорний елемент  Ділимо на нього друге рівняння системи (2.17):
Ділимо на нього друге рівняння системи (2.17):


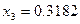
 (2.18)
(2.18)
 в передостаннє рівняння системи (2.18) і знаходимо:
в передостаннє рівняння системи (2.18) і знаходимо:

 .
.


