
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розробка програми інтерполяції функційСодержание книги
Поиск на нашем сайте
Мета роботи: Закріплення знань із застосування інтерполяційних формул, розробка комп’ютерної програми на мові Pascal, яка реалізує інтерполяційну формулу Лагранжа, застосування її для розв’язання індивідуального завдання. Теоретичні відомості Інтерполяція застосовується до функцій, які задані таблично, або які мають складні аналітичні вирази і обчислення Їх значень при довільному значенні аргумента на заданому відрізку неможливе або занадто складне. При цьому виконується приблизна заміна таких функцій функцією простої структури. Спрощена задача інтерполяції функції однієї змінної
Необхідно визначити функцію F(x), яка в точках хі має ті ж значення, що і функція f(x), тобто:
y1 y2
f(x) F(x)
x0 x1 x2 xn X
Для забезпечення однозначності розв’язання задачі інтерполяції, функцію F(x) можна вибрати у вигляді полінома Pn(x) ступеня не вищого n, який задовольняє умовам (6.1):
Цей інтерполюючий поліном Pn(x) зазвичай використовується для приблизного обчислення значень функції f(x) при значеннях х, відмінних від заданих вузлів інтерполяції хі (і=0,….n). У цьому занятті для інтерполяції функції використовується інтерполяційний поліном Лагранжа:
де x0, x1,..., xі,... xn - задані вузли інтерполяції, y0, y1,....yі, ….yn - відомі значення функції, що інтерполюється цих вузлах. При заданому (n+1) вузлі інтерполяції, що довільно розташовані на відрізку [ а, в ], поліном Ln(х) повинен мати в цих точках ті ж значення, що і функція, що інтерполюється
y0 y1 yn
x0=а x1 y2 xn=b
Поліном Лагранжа має загальний характер, застосовується при довільному розташуванні вузлів інтерполяції на заданому відрізку [ а, в ]. При n=1 формули Лагранжа (6.3) перетворюється на рівняння прямої лінії, яка проходить через 2 точки:
у
х1
х0 х1 х0 х2 у1
При n=2 отримуємо рівняння параболи, яка проходить через 3 точки:
Приклад інтерполяції функції поліномом Лагранжа Для функції y=cos х0=0; х1=0,25; х2=0,5; х3=1. Обчислюємо точні значення функції у вузлах інтерполяції:
Застосовуємо формулу (6.3) і отримуємо:
Сформований вираз є інтерполюючим поліномом Лагранжа для заданої функції y=cos Обчислимо значення поліному L3 у вузлах інтерполяції і порівняємо їх з точними значеннями:
Значення функції, що інтерполюється, і інтерполюючого поліному у вузлах інтерполяції співпадають, тобто обидві криві проходять через задану систему точок. Обчислимо значення функції
Інтерполяційний поліном дає значення, що незначно (похибка Алгоритмічна та програмна реалізація інтерполяційного полінома Лагранжа Функція
Обчислити наближене значення функції у точці х=хр, використовуючи для інтерполяції формулу Лагранжа.
i=0, n
k=0,n
Так
Ні
Var Хp,L1,L2,L: real; n,I,k: integer; Х,У:arrary [0..30] of real; Label M; Begin <Введення вихідних даних> L:=0; For i:=0 to n do Begin L1:=Y[i]; L2:=1; For k:=0 to n do Begin If i=k then goto M; L1:=L1*(Хp-Х[k]); L2:=L2*(Х[i]-Х[k]); M: end; L:=L+L1/L2; End; <Виведення результатів> Примітки: 1. Вихідними даними для роботи програми є масив вузлів інтерполяції Х, масив значень функції у цих точках У, кількість відрізків інтерполяції n (при цьому кількість вузлів інтерполяції n+1) і значення х=хр, при якому обчислюється значення функції; 2. Змінні L1, L2, L використовуються для значень, відповідно, чисельника, знаменника і полінома. Вони обчислюються за формулою (6.3). Порядок виконання роботи 1. Вибрати індивідуальне завдання. Номер варіанту у таблиці 6.1. відповідає номеру студента у списку групи; 2. Ознайомитися з теоретичним матеріалом з питань інтерполяції і апроксимації функцій; 3. Вибрати інтервал [ a,b ] і чотири вузли інтерполяцій в ньому х0, х1, х2, і х3, обчислити значення заданої функції у цих точках у0, у1, у2, у3. По цим даним сформувати інтерполяційний поліном Лагранжа L3; 4. Визначити значення полінома у вузлах інтерполяції, порівняти їх з точними значеннями функції уі; 5. Обчислити значення заданої функції і поліному при 10 значеннях х, що не співпадають з вузлами інтерполяції ( 6. Скласти докладний алгоритм інтерполяції функції поліномом Лагранжа; 7. Скласти і відлагодити програму на мові програмування Pascal, яка реалізує введення вихідних даних; обчислення значення функції, заданої таблично, при довільному значенні n і хр; виведення результатів у зручній формі на екран і в файл; 8. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо); 9. З використанням розробленої програми повторити пункти 4 і 5, порівняти результати; 10. Обчислити точне значення функції Визначити і порівняти похибку інтерполяції. Результати оформити у вигляді таблиці. Побудувати графік залежності похибки інтерполяції ∆ від кількості вузлів інтерполяції (і порядку поліному Лагранжа) n: ∆=f(n), для кожного значення хрі; 11. Сформулювати висновки по роботі.
Результати виконання кожного пункту завдання докладно описати у звіті по роботі.
Таблиця 6.1. Варіанти завдань до заняття № 6
Заняття № 7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.007 с.) |

 полягає у наступному. Функція
полягає у наступному. Функція  задана таблично, тобто на відрізку [ а,в ] задано (n+1) точку х0, х1, х2,….., хn і відомі значення функції у цих точках:
задана таблично, тобто на відрізку [ а,в ] задано (n+1) точку х0, х1, х2,….., хn і відомі значення функції у цих точках: ,
,  , ……,
, ……,  .
. , (6.1)
, (6.1)
 Точки хі (і=0, …, n) називаються вузлами інтерполяції, функція F(x) - інтерполююча функція. Графічно це означає, що крива у=F(x) повинна проходити через задану систему точок Mi (xi, yi), і=0,…n, тобто в цих точках вона повинна співпадати із функцією
Точки хі (і=0, …, n) називаються вузлами інтерполяції, функція F(x) - інтерполююча функція. Графічно це означає, що крива у=F(x) повинна проходити через задану систему точок Mi (xi, yi), і=0,…n, тобто в цих точках вона повинна співпадати із функцією 

 Y yn
Y yn




 y0
y0

 ,
,  , …,
, …,  . (6.2)
. (6.2)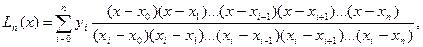 (6.3)
(6.3) , у
, у :
: Ln(xi)=yi; i=0,1,…, n.
Ln(xi)=yi; i=0,1,…, n.





 x2
x2




 x
x



 .
. у
у

 у0 у1 у0 у2
у0 у1 у0 у2

 х х
х х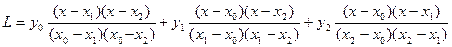
 сформувати інтерполяційний поліном Лагранжа, обравши вузли інтерполяції:
сформувати інтерполяційний поліном Лагранжа, обравши вузли інтерполяції:

 і поліному L3 при значеннях х, що не співпадають з вузлами інтерполяції (
і поліному L3 при значеннях х, що не співпадають з вузлами інтерполяції ( ):
):
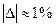 ) відрізняються від точних. При збільшенні кількості заданих вузлів інтерполяцій n і, відповідно, порядку полінома Ln збільшується і точність результату.
) відрізняються від точних. При збільшенні кількості заданих вузлів інтерполяцій n і, відповідно, порядку полінома Ln збільшується і точність результату. задана множиною точок з координатами хі і уі (і=0,…n):
задана множиною точок з координатами хі і уі (і=0,…n):


 Xp, L
Xp, L















 ) і значення поліному Ln в них (з використанням програми) при 5, 8, 10, 14, 17 і 20 вузлах інтерполяції, що розташовані в межах інтервалу [ a,b ]. При цьому можна використати результати п. 3 і 5.
) і значення поліному Ln в них (з використанням програми) при 5, 8, 10, 14, 17 і 20 вузлах інтерполяції, що розташовані в межах інтервалу [ a,b ]. При цьому можна використати результати п. 3 і 5.




