
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о числовых хар-ках, их применение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть даны 2 СВ Х и У и известны M[x] и M[y],σx и σy
1. Матожидание СВ С равно самой этой величине. M[C] = C Пусть Х – дискретная, (х=С, p=1), тогда M[C] = xp = 1*C = C
2. Дисперсия неслучайной величины С=0 D[C] = M[(C – M[C])2] = 0
3. Вынесение неслучайной величины за знак мат. ожидания M[CX] = C*M[X]
4. Вынесение неслучайной величины за знак дисперсии и СДО D[CX] = C2*D[X] σ[CX] = |C|*σ[X]
5. Матожидание суммы случайных величин (независимо от того, зависимы они или нет) M[X+Y] = M[X] + M[Y]
6. Матожидание линейной функции M[aХ + bY + c] = aM[X] + bM[Y] + c
7. Дисперсия суммы случайных величин D[X+Y] = D[X] + D[Y] – 2kxy Если х,у некоррелированы, то kxy=0, тогда D[X+Y] = D[X] + D[Y]
8. Дисперсия линейной функции D[aX + bY + c] = a2D[X] + b2D[Y] – 2ab* kxy kxy = M[XY] – m[x]*m[y] – корреляционный момент
9. Матожидание произведения СВ M[XY] = M[X] * M[Y] + kxy
10. Дисперсия произведения независимых СВ D[XY] = D[X] * D[Y] + M[X]2 * D[Y] + M[Y]2 * D[X] Для центрированных (M[X]=M[Y]=0) – D[
Применение теорем: 1) Доказать, что СВ связаны линейной функциональной зависимостью Y=aX+b 2) Определить М(Х) числа появлений события при нескольких опытах 3) Найти дисперсию числа появлений события при нескольких независимых и зависимых опытах 4) Средний расход средств до достижения числа опытов до k-го появления события (M(X)=ΣM(Xi)=k/p, D(X)=ΣD(Xi)=kq/p2, σ=(√kq)/p
19. Предельные теоремы теории вероятностей. Неравенство Чебышева, неравенство Маркова. Закон Больших чисел (теорема Чебышева). Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого свойства случайных явлений является закон больших чисел. Закон больших чисел: В широком – при большом числе СВ их средний результат перестает быть случайным и м.б. предсказан с большой степенью определенности В узком – ряд матем. теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
В основе качественных и количественных утверждений закона больших чисел лежит неравенство Чебышева. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.
Неравенство Чебышева – каково бы ни было «+»-е число α, РА, что величина Х отклонится от своего М(Х) не меньше, чем на α, ограничена сверху величиной D(X)/α2.
Неравенство Чебышева для некоторых СВ:
2) Для частости m/n события в n независимых испытаниях, в каждом из кот. оно может произойти с одной и той же p=M(m/n), и имеющей D(m/n)=pq/n:
Т.к. события x>A и х≤А противоположные, то заменяя выражение Р(x>A) выражением 1-Р(X≤A), придем к другой форме неравенства Маркова: Р(x≤A)≤1-[М(Х)t/Аt].
Теорема Чебышева. Если Х1,…, Хn – попарно независимые СВ, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было «+»-е число ε, вероятность неравенства равенства
будет как угодно близка к 1, если число СВ будет достаточно велико. Другими словами:
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых СВ, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического СВ от среднего арифметическогого их матожиданий будет по абс. величине сколь угодно малым.
Сущность теоремы заключается в том, что отдельные СВ могут иметь значительный разброс, а их среднее арифметическое рассеяно мало. Среднее арифметическое достаточно большого числа независимых СВ (дисперсии которых равномерно ограничены) утрачивает характер СВ.
Также эта теорема устанавливает связь между средним арифметически наблюдаемых значений СВ и ее M(X).
Рассмотрим СВ Х с M(X) и D(X). Над этой величиной производится n независимых опытов и вычисляется сред. арифм. всех наблюдаемых значений СВ. Требуется найти числовые характеристики сред. арифм. Само сред. арифметическое:
20. Следствия закона больших чисел (см. вопр. 19 ): теоремы Бернулли и Пуассона. Закон больших чисел: В шир. – при большом числе СВ их средний рез-т перестает быть случайным и м.б. предсказан с большой ст. определенности В узком – ряд матем. теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних хар-к большого числа испытаний к некот. определенным постоянным.
Пусть мы производим n независимых опытов, в каждом может появиться некоторое событие А, вероятность которого в каждом опыте равна p.
Смысл т.Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодной мало отличается от неслучайной величины p – вероятности события, т.к. практически перестает быть случайной. Замечание. Т.Бернулли является следствием теоремы Чебышева, ибо частость события можно представить как сред. арифм. n независимых альтернативных СВ, имеющих один и тот же закон распределения. (!) Т.Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, полученной в n повторных испытаниях, проводимых при одном и том же комплексе условий. Например, если PA рождения мальчика неизвестна, то в качестве ее значения мы можем принять частость этого события. Непосредственным обобщением т.Бернулли является т.Пуассона, когда вероятности события в каждом испытании различны. Теорема Пуассона. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти соответственно с вероятностями p1,…,pn, при неограниченном увеличении числа n сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях, т.е.:
Важная роль закона больших чисел в теоретическом обосновании методов матстатистики и ее приложений обусловила проведение ряда исследований, направленных на изучение общих условий применимости этого закона к последовательности СВ.
Например, тем-ра t воздуха в Москве Xi (i=1,…,365) каждый день года – величины случайные, подверженные существенным колебаниям в течение года, причем зависимые, т.к. на погоду каждого дня, очевидно, заметно влияет погода предыдущих дней. Однако среднегодовая тем-ра
21. Центральная предельная теорема и особая роль нормального распределения. Формулы для практического применения теории вероятностей (интегральная теорема Муавра-Лапласа).
Предельные законы распределения составляют предмет группы теорем под названием «Центральная предельная теорема», которую иногда называют «количественной формой закона больших чисел». Все формы ЦПТ посвящены установлению условий, при которых возникает НЗР. Так как эти условия на практике весьма часто выполняются, НЗР является самым распространенным из законов распределения, наиболее часто встречающимся в случайных явлениях природы. Он возникает во всех случаях, когда исследуемая СВ м.б. представлена в виде сумма достаточно большого числа независимых (или слабо зависимых) элементарных слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму.
Наиболее простой формой ЦПТ является следующая: Если Х1, Х2, …, Хn – независимые СВ, имеющие один и тот же закон распределения с матожиданием m и дисперсией σ2, то при неограниченном увеличении n закон распределения суммы Yn=Σnk=1Xk неограниченное приближается к нормальному.
Центральная предельная теорема – если СВ Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
Теорема Ляпунова. Если X1,…, Xn - независимые СВ, у каждой из которых существует M(Xi)=а, D(Xi)=σ2, абсолютный центральный момент третьего порядка M(|Xi-ai|3)=mi и
В практических задачах часто применяют ЦПТ для вычисления вероятности того, что сумма нескольких СВ окажется в заданных пределах.
Пусть X1, X2, …, Xn – независимые СВ с матожиданиями m1, … mn, и дисперсиями D1,… Dn,. Предположим, что условия ЦПТ выполнены (величины X1, X2, …, Xn сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых n достаточно для того, чтобы закон распределения величины Yn=Σnk=1Xk можно было бы считать нормальным. Тогда вер-ть того, что СВ У попадет в пределы участка (α;β):
Таким образом, для того, чтобы приближенно найти вероятность попадания суммы большого числа СВ на заданный участок, не требуется знать законы распределения этих величин; достаточно знать лишь их характеристики. Разумеется, это относится только к случаю, когда выполнено основное условие ЦПТ – равномерно малое влияние слагаемых на рассеивание суммы.
Частный случаем ЦПТ для дискретных СВ – теорема Лапласа: Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью p, то справедливо соотношение:
Где Y – число появлений события А в n опытах, q=1-p.
Интегральная теорема Муавра-Лапласа. Если p наступления события А в каждом испытании постоянная и отлична от 0 и 1, то РА, что число m, наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n прибл. равна:
Вышеуказанная формула – ф-ла Муавра-Лапласа. Чем больше n, тем она точнее. При выполнении условия npq≥20 она дает, как правило, удовл-ю для практики погрешность вычисления вер-тей.
Свойства функции: 1. Ф(х) – четная, т.е. Ф(-х)=Ф(х) 2. Ф(х) – монотонно возрастающая, причем при х→+∞ Ф(х)→1 (практически можно считать, что уже при x>4 Ф(х)~4) Следствие интегральной теоремы Муавра-Лапласа: Если p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний Ра, что: а) число m наступлений события А отличается от произведения np не более, чем на величину ε>0 (по абсолютной величине), т.е. б) частость m/n события А заключается в пределах от α до β (вкл)
в) частость m/n события А отличается от его p не более, чем на величину ∆>0 (по абс. величине):
Основные понятия математич. статистики. Простая статистическая совокупность. Статистическая функция распределения. Статистический ряд. Полигон. Гистограмма.
Разработка методов регистрации, описания и анализа математических экспериментальных данных получается в результат наблюдения массовых случайных явлений, составляющих предмет математической статистики (МС). Основные задачи МС: 1) Определение закона распределения СВ по стат.данным 2) Проверка правдоподобности гипотезы 3) Нахождения неизв-х параметров равномерного распределения Современную МС определяют как науку о принятии решений в условиях неопределенности. Главная задача МС состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Предположим, что СВ Х производит ряд опытов с целью определения либо закона ее распределения (заранее неизвестного), либо с целью проверки гипотезы о законе распределения. В каждом из опытов СВ Х принимает определенное значение – варианту. Причем последовательность x1,…xn значений СВ Х (где x1<…<xn) получена в результате ранжирования (операции расположения СВ по возрастанию).
Совокупность вариант представляет первичный стат. материал и называется простой стат. совокупностью или статистическим рядом. Обычно эти данные представлены в виде таблицы. На их основе строится функция распределения. Стат. функция распределения представляет собой ступенчатую функцию. Величина скачка данной функции – частота события при неограниченном числе опытов. Частота событий будет стремиться к подлинной.
Стат. ф-я распределения – функция F*(x), определяющая для каждого значения х относительную частоту события Х<x. F*(x)=nx/n, где nx - число вариант, меньших х, n – объем выборки.
Свойства стат. ф-и распределения: 1) значения функции принадлежат отрезку [0;1]
2) F*(x) – неубывающая функция 3) если х1 – наименьшая варианта, то F*(x)=0 при x≤x1; если хk – наибольшая варианта, то F*(x)1 при x>xk. Пример. Построить функцию F*n(x), если
Выборочная совокупность (выборка) – совокупность случайно отобранных объектов. Генеральная совокупность – совокупность объектов, из которых производится выборка. Объем совокупности – число объектов это совокупности.
Числа ni, показывающие сколько раз встречаются варианты xi в ряде наблюдений, называются частотами, а отношение их к объему выборке – частостями, т.е. p*i=ni/n. Для наглядности стат.распределение изображается графически в виде полигона и гистограммы. Полигон, как правило, служит для изображения дискретного (т.е. варианты отличаются на постоянную величину) стат. ряда.
Полигон является стат. аналогом многоугольника распределения (см. вопрос 7).
Для непрерывного распределения признака (т.е. варианты могут отличаться на сколь угодно малую величину) можно построить полигон частот, взяв середины интервалов в качестве значений
Площадь гистограммы частот = объему выборки, частностей = 1. Гистограмма частостей:
Гистограмма частот является стат.аналогом дифференциала функции распределения (плотности) f(x) СВ Х. Сумма площадей прямоугольников равна 1: h*p1*/h + … + pi*/h = pi* + … + pi* = 1, что соответствует условию Если соединить середины верхних оснований прямоугольников с отрезками прямой, то получим полигон того же распределения.
Точечные оценки параметров распределения. Требования, предъявляемые к точечным оценкам. Оценки для М(Х), D(X) и СДО. Большинство практических задач, которые решает статистика, состоит в оценивании некоторого количественного признака генеральной совокупности (совокупности объектов, явлений или процессов, из которых производится выборка). Предположим, что исследователю удалось установить, какому именно закону распределения подчиняется изучаемый количественный признак. В этом случае необходимо оценить параметры, которыми определяется предполагаемое распределение. Например, если удалось установить, что количественный признак подчиняется показательному закону распределения вероятностей, тогда необходимо оценить параметр λ, которым определяется данное распределение. Предположим, что имеются данные выборки, например, значения количественного признака x1, x2, …, xn, полученные в результате n наблюдений. Будем рассматривать x1, x2, …, xn как независимые СВ Х 1, Х 2, …, Х n. Статистическая оценка неизвестного параметра теоретического распределения – это функция от наблюдаемых случайных величин. Таким образом, определить статистическую оценку неизвестного параметра теоретического распределения, значит, определить функцию от наблюдаемых СВ Х 1, Х 2, …, Х n, которая дает приближ. значение оцениваемого параметра. Для того чтобы статистические оценки θi можно было бы принять за оценки параметров θi, необходимо и достаточно, чтобы оценки θi удовлетворяли трем статистическим свойствам: несмещенности, состоятельности и эффективности. θi называется несмещенной оценкой для параметра θi, если ее выборочное матожидание равно оцениваемому параметру генеральной совокупности. М(θi) = θi, М(θi) – θi = φi, где φi, - это смещение оценки. Смещенная оценка – это оценка параметра, чье матожидание не равно оцениваемому параметру, т.е. М(θi)≠θi, φi≠0.
θi является состоятельной оценкой для параметра θi, если она удовлетворяет закону больших чисел. Закон больших чисел гласит о том, что с увеличением выборки значение оценки θi стремится к значению параметра θi генеральной совокупности: Р(| θi – θi |<ε) → 1 при n → ∞. Для определения состоятельности оценки достаточно выполнения двух условий: 1) φi=0 или φi→0 при n→∞ - смещение оценки равно нулю или стремится к нему при объеме выборки, стремящейся к бесконечности. 2) D(θi) →0 при n→∞ - дисперсия оценки параметра θi стремится к нулю при объеме выборки, стремящемся к бесконечности. θi является эффективной оценкой для параметра θi, если статистическая оценка θi имеет наименьшую возможную дисперсию при заданном объеме выборки n.
Точечные оценки параметров распределения: Рассмотрим выборку x=(x1, x2, …, xn) значений генеральной совокупности Х. Пусть М(Х)=а, D(X)=σ2 генеральная средняя и дисперсия совокупности.
В качестве оценки для М(Х) используется выборочная средняя (средняя арифметическая выборки):
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику – выборочную дисперсию. В качестве оценки для D(Х) используется выборочная дисперсия: Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.
Выборочным средним квадратическим отклонением называют кв.корень из выборочной дисперсии: σ x =√σ x 2. x является несмещенной, состоятельной и эффективной оценкой для М(Х), причем σ Х 2=σ2/n. M(S2)=(n-1)/n*D(X), т.е. оценка S2 является смещенной. Чтобы избавиться от этого недостатка, для оценки неизвестной дисперсии генеральной совокупности пользуются исправленной несмещенной оценкой: При больших n (n>30) неизвестные параметры в формулах для дисперсии можно заменить на их выборочные без особой погрешности.
Метод моментов для нахождения точечных оценок неизв. параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденным по выборке. Так, если распределение зависит от одного параметра (например, задан вид плотности распределения f(х,0)), то для нахождения его оценки надо решить относительно θ одно ур-е: М(Х)= θ В (
Метод моментов является наиболее простым методов оценки параметров. Оценки метода моментов обычно состоятельны, однако их эффективность часто значительно меньше единицы. Пример. Найти оценки параметров СВ X~N(a,σ2). Требуется по выборке x1,…,xn найти точечные оценки неизвестных параметров a=M(X)=θ1 и σ2=D(X)=θ2. По методу моментов приравниваем их соответственно к выборочному среднему и выборочной дисперсии (α1=М(Х) – нач. момент 1 порядка, µ2=D(X) – центр. момент 2 порядка). Получаем
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.80 (0.017 с.) |

 ] = D[
] = D[  ] * D[
] * D[ 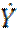 ]
]
 Для любой СВ, имеющей М(Х) и D(X), справедливо неравенство:
Для любой СВ, имеющей М(Х) и D(X), справедливо неравенство: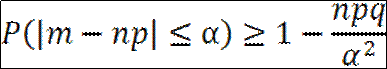 1) Для СВ X=m при Х~Bi(n,p) c M(X)=np и D(X)=npq:
1) Для СВ X=m при Х~Bi(n,p) c M(X)=np и D(X)=npq: В частности, есть обобщенное неравенство Чебышева: неравенство Маркова – если СВ Х принимает только неотрицательные значения и М(Х), то для любого «+»-го числа А верно неравенство:
В частности, есть обобщенное неравенство Чебышева: неравенство Маркова – если СВ Х принимает только неотрицательные значения и М(Х), то для любого «+»-го числа А верно неравенство:
 .
.


 Теорема Бернулли: при неограниченном увеличении числа опытов n частость события А сходится по вероятности к его вероятности в отд. испытании, т.е.
Теорема Бернулли: при неограниченном увеличении числа опытов n частость события А сходится по вероятности к его вероятности в отд. испытании, т.е.
 почти не меняется для Москвы в течение многих лет, являясь практически неслучайной, предопределенной.
почти не меняется для Москвы в течение многих лет, являясь практически неслучайной, предопределенной. , то закон распределения суммы Yn= X1+…+ Xn при n→∞ неограниченно приближается к нормальному с матожиданием
, то закон распределения суммы Yn= X1+…+ Xn при n→∞ неограниченно приближается к нормальному с матожиданием  и дисперсией
и дисперсией  .
.



 , где
, где  – функция (или интеграл вероятностей) Лапласа;
– функция (или интеграл вероятностей) Лапласа;
 , где
, где 





 Полигон частот – ломаная, отрезки которой соединяют точки с координатами (x1,n1),…,(xk,nk); полигон частостей (на рис.) – с координатами (x1,p1*),…,(xk,pk*). Варианты откладываются на оси абсцисс, а частоты и частости – на оси ординат.
Полигон частот – ломаная, отрезки которой соединяют точки с координатами (x1,n1),…,(xk,nk); полигон частостей (на рис.) – с координатами (x1,p1*),…,(xk,pk*). Варианты откладываются на оси абсцисс, а частоты и частости – на оси ординат.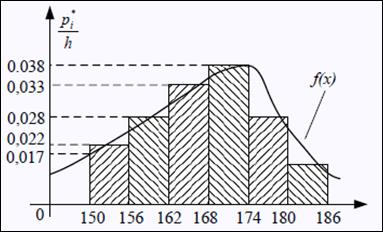 x1,…,xk. Гистограммая частот (частостей) – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/n. Плотность частоты – ni/h, частости – pi*/h.
x1,…,xk. Гистограммая частот (частостей) – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/n. Плотность частоты – ni/h, частости – pi*/h. для плотностей вероятностей f(x) (см. вопрос 11)
для плотностей вероятностей f(x) (см. вопрос 11) . Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.
. Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней. . Вычисление дисперсии можно упростить, используя формулу: S2= x2 - (x)2.
. Вычисление дисперсии можно упростить, используя формулу: S2= x2 - (x)2.

 есть функция от θ).
есть функция от θ). Если распределение зависит от двух параметров (например, вид плотности распределения f(x,θ1,θ2)) – надо решить относительно θ1 и θ2 систему уравнений:
Если распределение зависит от двух параметров (например, вид плотности распределения f(x,θ1,θ2)) – надо решить относительно θ1 и θ2 систему уравнений:  И, наконец, если надо оценить n параметров θ1, θ2, …, θn, - надо решить одну из систем вида:
И, наконец, если надо оценить n параметров θ1, θ2, …, θn, - надо решить одну из систем вида:
 Таким образом, искомые оценки параметров: θ1 =хВ и θ2 =√DВ.
Таким образом, искомые оценки параметров: θ1 =хВ и θ2 =√DВ.


