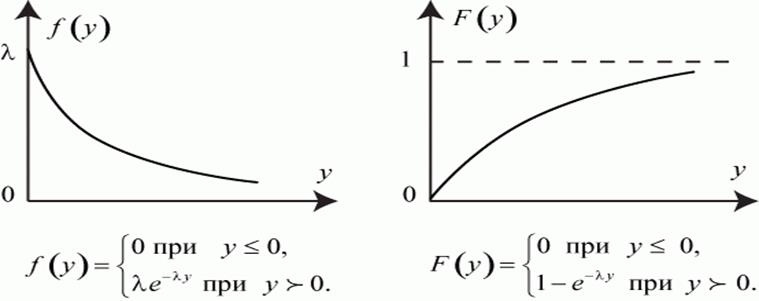
Показательный закон распределения вероятностей. Определение, графики плотности вероятности и функции распределения. Основные характеристики.

x~E(𝜆) – абсолютное непрерывное распределение с параметром 𝜆>0 и плотностью (левый график):

M(X) = σ_х = 1/𝜆 Мо = 0 S_k = 2

D(X) = 1/𝜆² Ме = (ln2)/𝜆 Ex = 6

Показательный закон распределения играет большую роль в теориях массового обслуживания и надежности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром 𝜆 – интенсивностью потока.

Теория массового обслуживания - раздел математики, изучающий системы, предназначенные для обслуживания массового потока требований случайного характера.

Т. надежности – наука, изучающая закономерности распред-я отказов техустройств, причины и модели их возн-я.

Особ. св-во: если промежуток времени Т, распределённый по показательному закону, уже длится некоторое время t, то это никак не влияет на закон распределения оставшейся части Т₁=Т-t промежутка, т. е. закон распределения Т₁ остаётся таким же, как и всего промежутка Т.

Понятие о системе случайных величин. Геометрическая интерпретация. Дискретный двумерный вектор. Совместные и частные законы распределения случайного вектора. Функция распределения, свойства. Условные законы распределения. Зависимые и независимые СВ.

 

Наряду с одномерными СВ рассматриваются многомерные СВ. Очень часто результат испытания характеризуется не одной СВ, а некоторой системой СВ, которую также называют многомерной СВ или случайным вектором. Например, точность попадания снаряда – координаты х и у – пример двумерной СВ.

Геометрическая интерпретация СВ:

1) Система двух СВ может изображаться такой на плоскости Оху, х – абсцисса, у – ордината

2) Систему двух СВ можно рассматривать как вектор на плоскости ху. Если ζ и η – дискретные СВ – вектор дискретный, если ζ и η – непрерывные, вектор непрерывный.

Дискретный двумерный вектор – геом. изображение СВ на плоск-ти Оху, Х и Y – составляющие этого вектора.

ζ	η
y1	…	ym
х1	p11		p1m
…
хm	pn1		pnm

 

Соотношение между возможными значениями случайного вектора и их вероятностям называется совместным законом распределения. Совместный закон распред-я дискретных СВ задается набором вероятностей p_ij одновременного осуществления событий p_ij=p(ζ=x_i; η=y_i) и представляется в виде таблицы:

Поскольку события {ζ=x_i; η=y_i} образуют полную группу, то получается:

Чтобы по таблице распределения найти вероятность того, что одномерная СВ примет определенное значение, надо просуммировать вероятности p_ij из соответствующей этому значению строки (столбца) данной таблицы.

Частным законом СВ ζ называется набор вероятностей событий {ζ=x}. Если задан совместный закон распределения, то частный получается следующим образом:

(суммируется строка) (суммируется столбец)

 

Функция распределения n-мерной СВ:

F(x₁, x₂, …, x_n) = P(X₁<x₁, X₂<x₂, …, X_n<x_n)

В двумерном случае для СВ (X,Y): F(x, y) = P(X< x, Y<y)

 

Геометрически функция распределения F(x,y) означает вероятность попадания случайной точки (X,Y) в заштрихованную область – бесконечный квадрат, лежащий левее и ниже точки М(x,y). Правая и верхняя границы области не включаются – это означает, что функция распределения непрерывна слева по каждому из аргументов.

 

В случае дискретной СВ ее функция распределения определяется по формуле:

(суммирование вер-тей распространяется на все i, для кот. x_i<x, и все j, для кот. y_j<y).

 

Свойства функции распределения:

1. F(x,y) не убывающая функция обоих своих аргументов, т.е. при x₁<x₂: F(x₁, y)≤F(x₂, y) и при y₁<y₂: F(x, y₁)≤F(x, y₂).

2. Повсюду на -∞ функция равна 0: F(-∞,y)=0, F(x,-∞)=0

3. При одном из аргументов, равном +∞, функция распределения (совместный закон распределения) превращается в функцию распределения СВ, соответствующей другому аргументу (частный з. распред-я):

F(+∞,y) = F₂(y) F(х,+∞) = F₁(x)

4. F(+∞,+∞)=1 5. 0≤F(x, y)≤1

 

Если зафиксировать значение одного из аргументов, например, положить Y=y_j, то полученное распределение СВ Х называется условным распределением Х при условии Y=y_j. Вероятности p_j(х_i) этого распределения будут условными вероятностями события Х=х_i, найденными в предположении, что событие Y=y_j произошло. Из определения условной вероятности:

Если величины независимы, то: F(x|y) = F₁(x); f(x|y) = f₁(x).

 

Аналогично условное распределение СВ Y при условии Х=х_i задается с помощью условных вероятностей:

F(x,y) = F₁(x)*F₂(y) – совместный закон распределения

 

СВ Х и У называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла друга. В противном случае Х и У – зависимые.

Для независимых СВ теорему умножения принимает вид: f(x,y)=f₁(x)f₂(y), т.е. плотность распределения системы независимых СВ равна произведению плотностей распределения отдельных величин, входящих в систему.

СВ ζ и η называются независимыми, если для любых множеств a и b выполняется усл-е: P(ζ?A,η?B) = P(ζ?A)*P(η?B). Дискретные СВ ζ и η независимы тогда и только тогда, когда события ζ=x_i и η=y_j независимы для всех значений x_i,y_j.