
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайная переменная и закон её распределения. Распределение хи-квадрат.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Переменная величина называется случайной, если свои возможные значения она принимает в рез-те некоторого опыта, и до его завершения не возможно предсказать какое точно значение она примет. З-н распределения дискретной случайной переменной- функция З-н распределения дискретной случайной переменной называется вероятностной функцией, значение которой равны вероятностям появления в опыте возможного значения сл. переменной: Закон распределения хи-квадрат случайной величины имеет вид(ХИ2РАСП,ХИ2ОБР):
10. Случайная переменная и закон её распределения. Распределение Стьюдента Квантиль, t крит уровня Переменная величина называется случайной, если свои возможные значения она принимает в рез-те некоторого опыта, и до его завершения не возможно предсказать какое точно значение она примет. З-н распределения дискретной случайной переменной- функция З-н распределения дискретной случайной переменной называется вероятностной функцией, значение которой равны вероятностям появления в опыте возможного значения сл. переменной: Закон распределения Стьюдента случайной величины имеет вид(СтьюдРАСП,СтьюдРаспОБР):
СтьюдРАСП-значение з-на распределения. Для расчёта tкрит используем ф-цию СтьюдРаспОБР(значение аргумента з-на распределения), глее вводим вероятность 1-
Ковариация Cov(x, y), и коэффициент корреляции, Cor(x, y) пары случайных переменных (x, y). Частная ковариация и частный коэффициент корреляции. Экономические переменные объекта (случайные или детерминированные), как правило, являются зависимыми величинами. Ковариации и коэффициент корреляции служат мерилами такой зависимости. Так, если (x, y) – пара случайных переменных (СП), то их ковариацией называется константа Cxy : Cxy = Cov(x, y) = E(x · y) – E(x) · E(y). (1) Свойства математического ожидания позволяют представить Cxy и так: Cxy = E((x–mx) · (y–my)), где mx = E(x), my = E(y). (2) Из формулы (1) видно, что для вычисления Cxy нужно знать закон распределения Pxy (q, r) пары (x, y). Если он неизвестен, что и бывает на практике, то ковариацию можно оценить по выборке из генеральной совокупности Xx,y: {(x1, y1), (x2, y2),... (xn, yn)}, (3) Оценкой ковариации служит величина
именуемая выборочной ковариацией. Каждая пара в выборке (3) имеет один и тот же закон распределения, Pxy (q, r); компонеты двух различных пар, например, (x1, y1) и (x2, y2) являются независимыми случайными переменными. Добавим, что случайные переменные (xi, xj) из выборки (3) обладают одинаковыми количественными характеристиками; аналогично, случайные переменных (yi,yj) имеют одинаковые количественные характеристики. Оценка (4) совершеннее оценки (5) в том смысле, что она обладает свойством несмещённости,
отсутствующим у оценки, которая, в силу данного обстоятельства, является смещённой оценкой ковариации. Наконец, отметим, что физическая размерность Cxy равна произведению физических размерностей СП x и y. Но часто удобно использовать безразмерную (нормированную) ковариацию rxy ,
которая именуется коэффициентом корреляции. Замечательно, что всегда –1 £ rxy £ +1, (7) причём если |rxy | = 1, то y = a0 + a1 · x. Так что при |rxy | = 1 между переменными (x, y) существует функциональная (жесткая) линейная зависимость. Если же Свойства 1. Операции ковариации и корреляции симметричны относительно своих аргументов; 2. Ковариация и корреляция между независимыми переменными равны 0; 3. 4. 5. 6. 7.
12. Случайная переменная и закон её распределения. Закон распределения Фишера. Квантиль, F крит уровня Опр1. Случайная величина Функция Опр2. Случайной называют переменную которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые невозможно заранее учесть. Опр3. Переменная x с областью изменения X называется случайной, если свои возможные значения q из множества X переменная x принимает в результате некоторого опыта со случайными элементарными исходами вида Закон распределения – функция Полной характеристикой СП служит её дифференциальный закон распределения (ЗР). Так называется функция Для дискретной величины Для непрерывной величины Закон распределения Фишера F распределение Плотность Или
Случайная переменная (СП) x именуется дискретной (ДСП), если множество X состоит из конечного или счётного количества констант qi, то есть X = {q1, q2,..., qn }. Если же X есть некоторый интервал числовой прямой, конечный или бесконечный, то есть X = (a, b), то СП x называется непрерывной (НСП). Пусть Случайная переменная
13. Случайный вектор и его основные количественные характеристики (на примере вектора Рассмотрим набор случайных переменных
Его основными характеристиками служат: 1) Вектор ожидаемых значений компонент:
так называют вектор констант, компоненты которого – мат. ожидания компонент вектора 2) Ковариационная матрица:
По главной диагонали располагаются дисперсии компонент случайного вектора. Недиагональные элементы это ковариации компонентов. Например,
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 906; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.008 с.) |

 скалярного аргумента q с областью определения
скалярного аргумента q с областью определения  , характеризующая возможность появления в опыте значений q случайной переменной x.
, характеризующая возможность появления в опыте значений q случайной переменной x.
 ,
,  , где m- кол-во степ.своб.
, где m- кол-во степ.своб. и её расчёт в Excel.
и её расчёт в Excel. , Г- гамма функция Эйлера, m- число степ.своб.
, Г- гамма функция Эйлера, m- число степ.своб. , и кол-во степеней свободы.
, и кол-во степеней свободы. (4)
(4) (5)
(5) , (6)
, (6) = 0, то связь между переменными x и y либо вообще отсутствует, либо же имеет место функциональная (жесткая), но нелинейная зависимость.
= 0, то связь между переменными x и y либо вообще отсутствует, либо же имеет место функциональная (жесткая), но нелинейная зависимость.

 ;
; ;
;

 и её расчёт в Excel.
и её расчёт в Excel. называется случайной величиной на вероятностном пространстве
называется случайной величиной на вероятностном пространстве  ,
,  .
. .
. скалярного аргумента q, определенная на всей числовой прямой, характеризующую объективную возможность появления в опыте значений q случайной переменной x.
скалярного аргумента q, определенная на всей числовой прямой, характеризующую объективную возможность появления в опыте значений q случайной переменной x. скалярного аргумента q, определённая на всей числовой прямой, характеризующая объективную возможность появления в опыте
скалярного аргумента q, определённая на всей числовой прямой, характеризующая объективную возможность появления в опыте 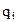 значений СП x. Если x – ДСП, то
значений СП x. Если x – ДСП, то 


 , где
, где  , – независимые случайные величины, распределённые по закону
, – независимые случайные величины, распределённые по закону  со степенями свободы
со степенями свободы  и
и 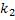 .
.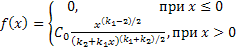 , где
, где 
 (с неотрицательной областью изменения
(с неотрицательной областью изменения 
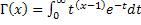 , Г(n+1)=n!, а
, Г(n+1)=n!, а  соответственно натуральные числа (параметры закона Фишера).
соответственно натуральные числа (параметры закона Фишера). - две независимые случайные переменные, имеющие
- две независимые случайные переменные, имеющие  распределение с числом степеней свободы n и m.
распределение с числом степеней свободы n и m. называется дробью Фишера, эта величина распределена по закону Стьюдента. Это позволяет при любом альфа вычислить
называется дробью Фишера, эта величина распределена по закону Стьюдента. Это позволяет при любом альфа вычислить  , удовлетворяющее уравнению
, удовлетворяющее уравнению 
 Эту величины также можно вычислить с помощь Excel, используя функцию FРАСПОБР по аргументам
Эту величины также можно вычислить с помощь Excel, используя функцию FРАСПОБР по аргументам  .
. левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке). . Этот упорядоченный набор называется случайным вектором и обозначается
. Этот упорядоченный набор называется случайным вектором и обозначается 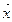 :
: (1)
(1)
 .
. (2)
(2) - это дисперсия компоненты
- это дисперсия компоненты  вектора (1). Элемент
вектора (1). Элемент  - это ковариация компонент
- это ковариация компонент  и
и  вектора (1) Матрица является симметричной.
вектора (1) Матрица является симметричной.


