
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
F-тест качества спецификации эконометрической модели.Содержание книги
Поиск на нашем сайте Рассмотрим модель:
Статистикой критерия гипотезы Здесь Если гипотеза (2) справедлива, а случайный остаток u в модели (1) обладает нормальным законом распределения, случайная переменная (3) имеет распределение Фишера (см. в конце) с количествами степеней свободы Этапы: 1) Вычислить величину (3); 2) Задаться уровнем значимости 3) Проверить справедливость неравенства Если оно справедливо, то гипотеза (2)принимается и можно сделать вывод о неудовлетворительном качестве регрессии, т.е. об отсутствии какой-либо объясняющей способности регрессоров в рамках модели (1). Если неравенство (5) несправедливо гипотеза (2) отклоняется в пользу альтернативы Закон распределения Фишера (F-распределение):
41. Процедура интервального прогнозирования по оценённой линейной эконометрической модели значений эндогенной переменной (на примере модели Оукена). Для построения интервально прогноза запишем дробь Это позволяет построить замкнутый промежуток
Модель Оукена:
1. В обучающую выборку включим наблюдения за 1997 -2002 года; в контролирующую – наблюдения 2003 года. 2. Оцененная модель:
Оценки модели вычисляются с помощью функции ЛИНЕЙН(
3. Вычислим при помощи оцененной модели (2) по значению Далее определим стандартную ошибку прогноза:
При доверительной вероятности
42. Процедура проверки адекватности оценённой линейной эконометрической модели (на примере модели Оукена). 1. Результаты наблюдений объекта следует разделить на два класса. В первый класс (обучающую выборку) включить основной объем результатов наблюдений 95% выборки. Оставшиеся результаты наблюдений (например, пара ( 2. По обучающей выборке 3. Задаться доверительной вероятностью 4. Проверить, попадают ли значения эндогенной переменной из контролирующей выборки в соответствующие доверительные интервалы (в интервал
Модель Оукена:
1. В обучающую выборку включим наблюдения за 1997 -2002 года; в контролирующую – наблюдения 2003 года. 2. Оцененная модель:
Оценки модели вычисляются с помощью функции ЛИНЕЙН(
3. Вычислим при помощи оцененной модели (2) по значению Далее определим стандартную ошибку прогноза:
При доверительной вероятности Если значение
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 (1)
(1) (2) против альтернативы
(2) против альтернативы  служит случайная переменная
служит случайная переменная  (3)
(3) – коэффициент детерминации (объясненная регрессорами в рамках обучающей выборки
– коэффициент детерминации (объясненная регрессорами в рамках обучающей выборки  доля эмпирической дисперсии эндогенной переменной
доля эмпирической дисперсии эндогенной переменной 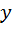 ); k – количество регрессоров в модели (1); n – объем обучающей выборки
); k – количество регрессоров в модели (1); n – объем обучающей выборки  , по которой оценена МНК-модель (1).
, по которой оценена МНК-модель (1).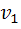 и
и  , где
, где  (4)
(4)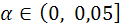 и при помощи функции FРАСПОБР Exel при количествах степеней свободы (4) отыскать
и при помощи функции FРАСПОБР Exel при количествах степеней свободы (4) отыскать  -квантиль распределения Фишера
-квантиль распределения Фишера  ;
; (5)
(5) где
где  - стандартное обозначение для гамма-функции Эйлера.
- стандартное обозначение для гамма-функции Эйлера. (1), имеющую смысл нормированной ошибки прогноза. Если случайный остаток в регрессионной модели не имеет автокорреляции и нормально распределен, то дробь (1) распределена по закону Стьюдента с числом степеней свободы
(1), имеющую смысл нормированной ошибки прогноза. Если случайный остаток в регрессионной модели не имеет автокорреляции и нормально распределен, то дробь (1) распределена по закону Стьюдента с числом степеней свободы  , где
, где 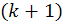 — количество оцениваемых коэффициентов модели.
— количество оцениваемых коэффициентов модели. , где:
, где:  , (2) именуемыйдоверительным интервалом, который накрывает прогнозируемое значение
, (2) именуемыйдоверительным интервалом, который накрывает прогнозируемое значение  с принятой доверительной вероятностью
с принятой доверительной вероятностью  .
.  — это критическое значение модуля дроби Стьюдента (двусторонняя
— это критическое значение модуля дроби Стьюдента (двусторонняя 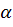 ,
,  при помощи функции СТЬЮДРАСПОБР.
при помощи функции СТЬЮДРАСПОБР.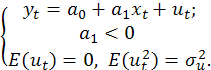 (1)
(1) (2)
(2) ;
;  ;1;1).
;1;1). ;
; 
 прогноз величины
прогноз величины  :
:  .
. , где
, где  . Так как модель Оукена – это модель парной регрессии, тo
. Так как модель Оукена – это модель парной регрессии, тo  можно вычислить по формуле:
можно вычислить по формуле:

 )) составят контролирующую выборку.
)) составят контролирующую выборку. оценить модель.
оценить модель. ;
; 



