
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарный временной ряд. Белый шум.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Временной ряд называется стационарным (в широком смысле) если его ожидаемое значение и дисперсия постоянны (не зависят от переменной времени t), а автоковариационная и автокор функция является четной функцией одного аргумента τ=i-j E(yt)=my(t), Var(yt)=
Временной ряд явл нестационарным, если не соблюдено хотя бы одно из этих условий. Требование стационарности: неизменность функции регрессии во времени, гомоскедастичность случ остатка. Спецификация общей модели стационарного ряда:
Белый шум Белый шум – простейший стац временной ряд со след спецификацией:
Оценка характеристик стационарного временного ряда. Ряд
Ряд 1) 2) 3) 4) Ряд
Рассмотрим основные характеристики временного ряда: 1) Математической ожидание ряда
2) Дисперсия временного ряда
3) Автоковариационная функция ряда
4) Автокорреляционная функция ряда
Оценки этих характеристик могут быть найдены по одной реализации этого ряда 1) Оценка математического ожидания:
2) Оценка дисперсии:
3) Оценка автоковариационной функции:
4) Оценка автокорреляционной функции:
Частная автокорреляционная функция стационарного временного ряда и алгоритм её оценивания. Рассмотрим уровни ряда ut на отрезке [t;t+ τ] (ut, ut+1, …, ut+ τ -1, ut+ τ) Удалим(при помощи уравнения регрессии) влияние членов ut, …, ut+ τ-1 из уровней ut и ut+ τ. После этого рассмотрим ковариацию остатков ut и ut+ τ. Это и будет частная автокорреляционная функция в точке τ.
Ϭuu(p)(τ)= На основании 2.10 дается определение частной автокорреляционной функции стационарного ряда ρuu(p)(τ)= Частная автокорреляционная функция белого шума имеет уравнение ρξξ(p)(τ)= ρξξ(τ)= Можно обосновать следующий алгоритм оценивания частной автокорреляционной функции ряда по его реализации: Оценить МНК параметры модели 1. 2. Принять оценкой ρuu(p)(τ) оценку βτ. Модель AR(p) и её идентификация. Начнем с простейшего и наиболее полезного для практики частного случая авторегрессии первого порядка
Непосредственно проверяется, что матожидание уровней ut=0 при любых t. Требование постоянной дисперсии приводит к следующему уровню, которому должны удовлетворять параметры модели. ρ должен быть <1. Непосредственно проверяется, что ρ имеет смысл коэффициента корреляции уровней ряда в соседние моменты времени. Также показывается, что автокорреляционная функция зависит только от расстояния между сечениями по правилу ρuu(i,j)=ρ|i-j|=ρτ Рассмотрев это правило констатируем, что корреляции сечений ряда снижаются по экспоненте расстояния τ между уровнями ряда. При ρ=0 ряд превращается в WN. Если ρ=1, то ряд становится нестационарным рядом, называющимся случайным блужданием. Справедлива теорема: Если utϵAR(1), то ρuu(p)(τ)= Модель задается рекурсивным уравнением ut=β1ut-1+ β2ut-2+…+ βput-p+ξt Коэффициенты удовлетворяют определенным ограничениям, чтобы ряд оказался стационарным. Модель MA(q) и её идентификация. Вначале рассмотри простейший случай
Теорема. Если utϵMA(1) то 1) utϵSTS 2) E(ut)=0, Ϭu2=Ϭξ2(1+γ2) 3) Ϭuu(τ)= Автокорреляционная функция ряда MA(1) как инструмент идентификации. ρuu(τ)= Данная функция служит инструментом идентификации модели MA(1). Подчеркнем, что эта функция может быть оценена по правилу ρyy(τ)= Рекурсивное уравнение модели: ut=γ1ξt-1+ γ 2ξt-2+…+ γ pξt-p+ξt Теорема. Если utϵMA(q) то ρuu(τ)=0 при τ>q.
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 878; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.250.15 (0.011 с.) |


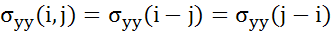 (ковариация зависит только от расстояния между уровнями)
(ковариация зависит только от расстояния между уровнями)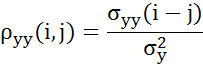


 именуется стационарным (в сильном смысле), если закон распределения вектора сечений этого ряда оказывается инвариантным относительно сдвига по времени этих сечений на любую величину
именуется стационарным (в сильном смысле), если закон распределения вектора сечений этого ряда оказывается инвариантным относительно сдвига по времени этих сечений на любую величину  .
.
 (расстояние между сечениями ряда):
(расстояние между сечениями ряда):



 именуется нестационарным, если хотя бы одно условие 1-4 не выполняется.
именуется нестационарным, если хотя бы одно условие 1-4 не выполняется. – некоторая детерминированная функция времени t. Для (1) математическим ожиданием является сумма тренда и сезонной составляющей.
– некоторая детерминированная функция времени t. Для (1) математическим ожиданием является сумма тренда и сезонной составляющей.
 – функция двух аргументов
– функция двух аргументов  при перестановке которых значения функций не меняются.
при перестановке которых значения функций не меняются.




 (2.10)
(2.10)



 финитная функция.
финитная функция.

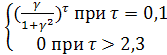
 . (над сигмами значки оценок).
. (над сигмами значки оценок).


