
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Стационарные cлучайные процессыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте СП Понятие стационарного случайного процессаССП. Стационарность в Узком и широком смыслах.
Значительное число происходящих в природе событий, в частности, связанных с эксплуатацией технических устройств, носит «почти» установившиейся характер, то есть картина таких событий, подверженных незначительным случайным флуктуациям, тем не менее, в целом с течением времени сохраняется. В этих случаях принятно говорить о стационарных случайных процессах. Например, летчик выдерживает заданную высоту полета, но разнообразные внешние факторы (порывы ветра, всходящие потоки, изменение тяги двигателей и т.п.) приводят к тому, что высота полета колеблется около заданного значения. Другим примером могла бы служить траектория движения маятника. Если бы он был предоставлен сам себе, то при условии отсутствия систематических факторов, приводящих к затуханию колебаний, маятник находился бы в режиме установившихся колебаний. Но различные внешние факторы (порывы ветра, случайные колебания точки подвеса и т.п.), не меняя в целом параметров колебательного режима, тем не менее делают характеристики движения не детерминированными, а случайными.
Стационарным (однородным во времени) называют случайный процессСП, статистические характеристики которого не меняются с течением времени, то естьт.е. являются инвариантными относительно временных и сдвигов. Различают случайные процессыСП стационарные в широком и узком смысле.
Стационарным случайным процессомССП в узком смысле называется случайный процесс ХСП x(t), все вероятностные характеристики которого не меняются со временем, то есть
Таких, что
Выполняется условие F(t1; t2;…;tn; x1; x2;…; xn)=F(t1+τ; t2+τ;…;tn+τ; x1; x2;…; xn), и, следовательно, все n-мерные распределения зависят не от моментов времени t1; t2;…;tn, а от n-1 длительности временных промежутков τi;:
В частности, одномерная плотность распределения вообще не зависит от времени t:
двумерная плотность сечений в моменты времени t1 и t2
n-мерная плотность сечений в моменты времени t1; t2...; tn:
Случайный процессСП Хx(t) называется стационарным в широком смысле, если его моменты первого и второго порядка инвариантны относительно временного сдвига, то есть его математическое ожидание не зависит от времени t и является константой, а корреляционная функция зависит только от длины временного промежутка между сечениями:
Очевидно, что стационарный случайный процессССП в узком смысле является стационарным случайным процессомССП и в широком смысле;, обратное утверждение не верно.
Свойства вероятностных характеристик стационарного случайного ПроцессаССП 1.
2.
4. Дисперсия стационарного случайного процесса ССП есть константа, равная знзнаачению ее корреляционной функции в точке
5.
6. Корреляционная функция стационарного случайного процессаССП является положительно определенной, то есть .е.
Нормированная корреляционная функция стационарного случайного процессаССП
Пример 11. Найти характеристики и сделать вывод о типе случайного процессаСП Хx(t):
гГде U1 иb U2 - некоррелированные случайные величиныСВ;
Решение.
Следовательно, случайный процесс Х(t) является стационарным в широком смысле. Как следует из Ппримера 10…,, если U1 и U2 независимые, центрирование и нормально распределенные случайные величиныСВ, то случайный процессСП
Пример 12. … Доказать, стационарность в широком смыслечто случайного процессаСП Хx(t) является стационарным в широком смысле:
где V
Решение. Запишем Хx(t) следующим образом:
Так как случайная величина
следовательно,
Получаем
Так как cлучайный процессСП Хx(t) имеет постоянные математическое ожидание и дисперсию, а корреляционная функция является функцией
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 799; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |











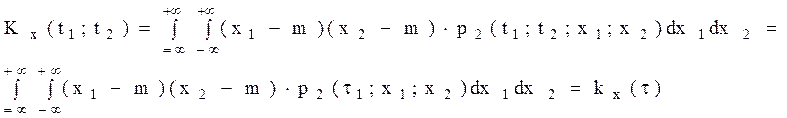 3. Корреляционная функция стационарного случайного процессаССП четна:
3. Корреляционная функция стационарного случайного процессаССП четна: поскольку она обладает следующей симметрией
поскольку она обладает следующей симметрией 
 :
:



 также четна, положительно определена и при этом
также четна, положительно определена и при этом








 также является стационарным в широком смысле.
также является стационарным в широком смысле.
 и
и  независимые случайные величиныСВ; MV=mvV - const;
независимые случайные величиныСВ; MV=mvV - const; 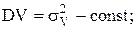
 случайная величинаСВ;
случайная величинаСВ; 








 , то вне зависимости от закона распределения случайной величиныСВ V М случайный процессСП Х x(t) является стационарным в широком смысле.
, то вне зависимости от закона распределения случайной величиныСВ V М случайный процессСП Х x(t) является стационарным в широком смысле.


