Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретный спектр стационарной случайной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
А. Частоты—произвольные числа, количество их конечно. Пусть стационарная случайная функция X (t)может быть представлена в виде спектрального разложения
причем сохраняются допущения, указанные в начале п. 2 (см. § 1). Найдем дисперсию одной гармоники Хi (t), учитывая, что случайные величины Ui и Vi, не коррелированы и дисперсии величин с одинаковыми индексами равны между собой: D (Ui) =D (Vi) = Di: D [ Xi (t)] =D [ Ui cos ωit + Vi sin ωit ]= D [ Ui cos ωit ]+ D [ Vi sin ωit ]=cos2 ωitD (Ui)+sin2 ωitD (Vi)= =(cos2 ωit +sin2 ωit) Di = Di. Итак, D [ Xi (t)] = Di. (* *) Таким образом, дисперсия i -й гармоники спектрального разложения (*) равна дисперсии случайной величины Ui или, что то же, дисперсии случайной величины Vi. Найдем теперь дисперсию стационарной случайной функции Х (t), приняв во внимание, что слагаемые Xi (t)не коррелированы (см. § 1) и поэтому дисперсия их суммы равна сумме дисперсий слагаемых (см. гл. XXIII, § 15, замечание 2):
Используя (**), окончательно получим
Итак, дисперсия стационарной случайной функции, которая может быть представлена в виде суммы конечного числа гармоник с произвольными частотами, равна сумме дисперсий составляющих ее гармоник. Дискретным спектром стационарной случайной функции Х (t) вида (*) называют совокупность дисперсий всех составляющих ее гармоник. Заметим, что поскольку каждой частоте ωi, можно поставить в соответствие дисперсию Di, то спектр можно изобразить графически: на горизонтальной оси откладывают частоты ωi, а в качестве соответствующих ординат ( их называют спектральными линиями) строят дисперсии Di. Этот дискретный спектр называют линейчатым. Пример. Построить дискретный спектр стационарной случайной функции X (t)=[ U1 cos2 t +V1sin2 t ]+[ U 2cos3 t + V sin23 t ]+[ U 3cos4 t + V 3sin4 t ], если случайные величины U 1, U 2, U 3; V1, V2, V2 не коррелированы, их математические ожидания равны нулю и заданы дисперсии: D (U 1)= D (V 1)=5, D (U 2)= D (V 2) =6, D (U 3)= D (V 3) =4. Решение. Отложив на горизонтальной оси частоты ω 1=2, ω 2=3, ω 3=4, а на вертикальной оси—соответствующие им ординаты D 1=5, D 2=6, D 3 =4, получим график искомого спектра. Б. Равноотстоящие частоты, множество их бесконечное (счетное). В предыдущем пункте предполагалось, что число частот в спектральном разложении (*) конечно, а сами частоты—произвольные числа. Теперь рассмотрим спектральное разложение вида
в котором число частот бесконечно (счетно), они равноотстоящие, причем разность любых двух «соседних» частот Δ ω=ωi+1 - ωi =π/ t (i = 1, 2, …), где Т— действительное положительное число. Таким образом,
Напишем корреляционную функцию [см. § 1, формула (***)] рассматриваемой стационарной случайной функции Х (t), положив ωi =πi/ T n =∞:
При τ=0, учитывая, что kx (0) =Dx, получим
Итак, дисперсия стационарной случайной функции, которая может быть представлена в виде суммы бесконечного (счетного) множества гармоник с равноотстоящими частотами, равна сумме дисперсий слагаемых гармоник (если сумма существует, т. е. ряд (**) сходится). Заметим, что соотношение (*) можно рассматривать как разложение корреляционной функции в ряд Фурье по косинусам. Из (*) видно, что kx (τ)—периодическая функция с периодом 2 Т, поэтому коэффициенты Фурье
или, учитывая, что ωi =π i / Т и подынтегральная функция - четная,
Если каждой частоте ωi =π i / T (i =1, 2,...) ставить в соответствие дисперсию Di, то получим, как и в случае конечного числа произвольных частот, дискретный линейчатый спектр, причем число спектральных линий (ординат D i) бесконечно (счетно) и они равноотстоящие (соседние спектральные линии находятся одна от другой на одном и том же расстоянии Δ ω =π/ T). Непрерывный спектр стационарной случайной функции. Спектральная плотность Среди стационарных случайных функций есть такие функции, корреляционные функции которых нельзя представить в виде
где число слагаемых конечно или счетно. Спектр этих функций не дискретный, а непрерывный. Для рассмотрения стационарных случайных функций с непрерывным спектром необходимо ввести понятие спектральной плотности. Выше, когда частоты гармоник спектрального разложения стационарной случайной функции были дискретными и равноотстоящими, был получен дискретный линейчатый спектр, причем соседние частоты отличались на величину Δ ω =π/ Т. Пусть Т→∞, тогда Δ ω →0. Ясно, что при этом частота изменяется непрерывно (поэтому обозначим ее через со без индекса), соседние ординаты спектра сближаются и в пределе вместо дискретного спектра мы получим непрерывный спектр, т. е. каждой частоте ω (ω ≥0) соответствует ордината, которую обозначим через s * x (ω). Хотя отрицательные частоты физического смысла не имеют, для упрощения вычислений целесообразно считать, что частоты изменяются в интервале (-∞,∞), и вместо функции s * x (ω) рассматривать функцию, которая имеет вдвое меньшие ординаты: sx (ω)= s*x (ω) Спектральной плотностью стационарной случайной функции Х (t) называют функцию sx (ω), которая связана с корреляционной функцией kx (τ) взаимно обратными преобразованиями Фурье:
Эти формулы называют формулами Винера—Хинчина. В действительной форме они представляют собой взаимно обратные косинус-преобразования Фурье:
Важное значение спектральной плотности состоит в том, что, зная ее, можно найти корреляционную функцию, и обратно (в этом смысле спектральная плотность и корреляционная функция эквивалентны); кроме того, как уже было указано, использование спектральной плотности в ряде случаев значительно упрощает теоретические и практические расчеты. Подчеркнем, что, как следует из формулы (***), спектральная плотность—четная функция: sx(- ω)=sx(ω). Выясним вероятностный смысл функции sx (ω).Положив τ=0 в соотношении (****) и учитывая, что kx (0) =Dx, sx (ω)—четная функция, получим
Видим, что дисперсия стационарной случайной функции Х (t) представляет собой «сумму» элементарных дисперсий sx (ω) dω = sx (ω)Δ ω; каждая элементарная дисперсия соответствует частичному интервалу частот Δ ω. В частности, частичному интервалу Δ ω=ωb - ωa соответствует дисперсия
По теореме о среднем, Dx= (ωa - ωb) sx (ωc) = Δ ωsx (ω c), где ωa < ωc < ωb Отсюда sx (ω c ) =Dx/ Δ ω. Из этой формулы заключаем: а) величину sx (ωc) можно истолковатькаксреднююплотность дисперсиина частичном интервале Δ ω, содержащем частоту ωс; б) при Δ ω →0 естественно считать, что sx (ωc) - плотность дисперсии в точке ωc. Поскольку никаких ограничений на частоту ωc наложено не было, полученный результат справедлив для любой частоты. Итак, спектральная плотность описывает распределение дисперсий стационарной случайной функции по непрерывно изменяющейся частоте. Из вероятностного смысла спектральной функции следует, что спектральная плотность—неотрицательная функция sx≥0. Пример 1. Найти спектральную плотность стационарной случайной функции X (t), зная ее корреляционную функцию
Решение. Используя формулу
и учитывая, что |τ| = τ в интервале (0, 2), имеем
Интегрируя по частям, окончательно получимискомуюспектральную плотность: sx (ωc) = sin2 ω /(π ω 2) Пример 2. Найти спектральную плотностьстационарнойслучайной функции Х (t), зная ее корреляционную функцию kx(τ)=De-α|τ|, α>0. Решение. Используем формулу
Учитывая, что |τ|= - τ при τ<0, |τ|=τ при τ≥0, получим kx (τ) =Dеατ при τ<0, kx (τ) = Dе-ατ при τ≥0. Следовательно,
Выполнив интегрирование, найдемискомую спектральную плотность:
Пример 3. Найти корреляционную функцию стационарной случайной функции Х (t), зная ее спектральную плотность
Решение. Используя формулу
и учитывая, что sx (ω)= ω 0 в интервале (0, ω 0), имеем
Выполнив интегрирование, получим искомую корреляционную функцию:
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.75 (0.01 с.) |






 …,
…, 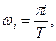
 (*)
(*) (**)
(**)

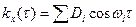 (Di > 0),
(Di > 0), (*)
(*)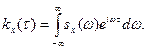 (**)
(**) (***)
(***) (****)
(****)