
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несмещенные, эффективные и состоятельные оценкиСодержание книги
Поиск на нашем сайте
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Ниже указаны эти требования. Пусть Θ* - статистическая оценка неизвестного параметра в теоретического распределения. Допустим, что по выборке объема п найдена оценка Θ1*. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку Θ1*. Повторяя опыт многократно, получим числа Θ1*, Θ1*,..., Θk*, которые, вообще говоря, различны между собой. Таким образом, оценку Θ* можно рассматривать как случайную величину, а числа Θ1*, Θ1*,..., Θk*-как ее возможные значения. Представим себе, что оценка Θ* дает приближенное значение Θ с избытком; тогда каждое найденное по данным выборок число Θi* (i = 1, 2,.... k)больше истинного значения Θ. Ясно, что в этом случае и математическое ожидание (среднее значение) случайной величины Θ* больше, чем Θ, т. е. М (Θ*) > Θ. Очевидно, что если Θ* дает оценку с недостатком, то М (Θ*) < Θ. Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому Параметру, привело бы к систематическим *) (одного знака) ошибкам. По этой причине естественно потребовать, чтобы математическое ожидание оценки Θ* было равно оцениваемому параметру. Хотя соблюдение этого требования не устранит ошибок (одни значения Θ* больше, а другие меньше Θ), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требований М (Θ*) = Θ гарантирует от получения систематических ошибок. Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. М (Θ*) = Θ. *) В теории ошибок измерений систематическими ошибками называют неслучайные ошибки, искажающие результаты измерений в одну определенную сторону. Например, измерение длины растянутой рулеткой систематически дает заниженные результаты. Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру. Однако было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения Θ* могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия D (Θ*) может быть значительной. В этом случае найденная по данным одной выборки оценка, например Θ1*, может оказаться весьма удаленной от среднего значения Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности. Состоятельной называют статистическую оценку, которая при n →∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n →∞ стремится к нулю, то такая оценка оказывается и состоятельной.
Генеральная средняя
Пусть изучается дискретная генеральная совокупность относительно количественного признака X. Генеральной средней Если все значения x 1, х 2, …, xN признака генеральной совокупности объема N различны, то
Если жезначения признака x 1, х 2, …, xk имеютсоответственно частоты N 1, N 2,..., Nk,причем N 1 +N 2 +…+Nk=N,то
т. е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам. Замечание. Пусть генеральная совокупность объема N содержит объекты с различными значениями признака X,равными x 1, х 2, …, xN. Представим себе, что из этой совокупности наудачу извлекается один объект. Вероятность того, что будет извлечен объект со значением признака, например x 1 очевидно, равна 1/ N. С этой же вероятностью может быть извлечен и любой другой объект. Таким образом, величину признака X можно рассматривать как случайную величину, возможные значения которой x 1, х 2, …, xn имеют одинаковые вероятности, равные 1 /N. Найдем математическое ожидание М (Х):
Итак, если рассматривать обследуемый признак X генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака:
Этот вывод мы получили, считая, что все объекты генеральной совокупности имеют различные значения признака. Такой же итог будет получен, если допустить, что генеральная совокупность содержит по нескольку объектов с одинаковым значением признака. Обобщая полученный результат на генеральную совокупность с непрерывным распределением признака X, и в этом случае определим генеральную среднюю как математическое ожидание признака:
Выборочная средняя
Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема п. Выборочной средней Если все значения x 1, х 2, …, xn признака выборки объема n различны, то
Если же значения признака x 1, х 2, …, xk имеют соответственно частоты n 1, n 2, …, nk, причем п 1 + п 2 +… + nk = n,то
или
т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам. Замечание. Выборочная средняя, найденная по данным одной выборки, есть, очевидно, определенное число. Если же извлекать другие выборки того же объема из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, а следовательно, можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения (его называют выборочным), в частности о математическом ожидании и дисперсии выборочного распределения. Заметим, что в теоретических рассуждениях выборочные значения x 1, х 2, …, xn признака X,полученные в итоге независимых наблюдений, также рассматривают как случайные величины Xl, X 2,..., Хn,имеющие то же распределение и, следовательно, те же числовые характеристики, которые имеют X.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 773; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 *, а значит, и от самого оцениваемого параметра Θ; приняв Θ1* в качестве приближенного значения Θ, мы допустили бы большую ошибку. Если же потребовать, чтобы дисперсия Θ* была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требование эффективности.
*, а значит, и от самого оцениваемого параметра Θ; приняв Θ1* в качестве приближенного значения Θ, мы допустили бы большую ошибку. Если же потребовать, чтобы дисперсия Θ* была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требование эффективности.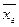 называют среднее арифметическое значений признака генеральной совокупности.
называют среднее арифметическое значений признака генеральной совокупности. .
. ,
,
 .
. .
.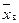 называют среднее арифметическое значение признака выборочной совокупности.
называют среднее арифметическое значение признака выборочной совокупности.
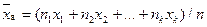 ,
, ,
,


