
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормированная спектральная плотностьСодержание книги
Поиск на нашем сайте
Наряду со спектральной плотностью часто используют нормированную спектральную плотность. Нормированной спектральной плотностью стационарной случайной функции Х (t) называют отношение спектральной плотности к дисперсии случайной функции:
Пример. Задана спектральная плотность sx (ω)=5/(π (1+ ω 2)) стационарной случайной функции Х (t). Найти нормированную спектральную плотность. Решение. Найдем дисперсию:
Найдем искомую нормированную спектральнуюплотность, для чего разделим заданную спектральную плотность на дисперсию Dx =5; в итоге получим
Нормированная спектральная плотность представима в виде косинус-преобразования Фурье нормированной корреляционной функции:
Действительно, чтобы получить эту формулу, достаточно разделить на Dx обе части соотношения (***) (см. § 3). В свою очередь, нормированная корреляционная функция выражается через нормированную спектральную плотность при помощи обратного преобразования Фурье:
В частности,положив τ=0 и учитывая, что ρx (0)=1, получим
Геометрически этот результат означает, что площадь, ограниченная снизу осью Oω и сверху кривой Взаимная спектральная плотность стационарных и стационарно связанных случайных функций Пусть X (t) и Y (t)—стационарные и стационарно связанные случайные функции со взаимной корреляционной функцией rxy (τ). Взаимной спектральной плотностью двух стационарных и стационарно связанных случайных функций Х (t)и Y (t) называют функцию sxy (ω), определяемую преобразованием Фурье: В свою очередь, взаимная корреляционная функция выражается через взаимную спектральную плотность с помощью обратного преобразования Фурье: Пример. Задана корреляционная функция kx (τ) стационарной случайной функции X (t). Найти: а) взаимную корреляционную функцию; б) взаимную спектральную плотность случайных функций X (t) и Y (t)= Х (t - t 0). Решение. а) Легко убедиться, что Y (t) — стационарная функция. Найдем взаимную корреляционную функцию:
Отсюда видно, что стационарные функции Х (t) и Y (t)стационарносвязаны (их взаимная корреляционная функция зависиттолькоотразности аргументов τ). б) Найдем взаимную спектральную плотность: Итак, искомая взаимная спектральная плотность Дельта-функция Дельта-функция δ (t) является примером обобщенной функции (обобщенная функция—предел последовательности однопараметрического семейства непрерывных функций). Дельта-функцию определяют тем условием, что она ставит в соответствие всякой непрерывной функции f (t) ее значение при t=0:
Правую часть равенства можно представить в виде предела:
где
Таким образом, дельта-функцию можно рассматривать как предел последовательности функций δε (t) при ε→0. Учитывая, что δε(t)→0 при t≠ 0, δε→∞ при t →0 и
Физически дельта-функцию можно истолковать как плотность единичной массы, сосредоточенной в нуле. Можно доказать, что дельта-функция представима интегралом Фурье:
Отсюда
Замечание. В приложениях часто используют соотношение,
которое вытекает из сказанного выше.
Стационарный белый шум Стационарным белым шумом называют стационарную случайную функцию Х (t), спектральная плотность которой постоянна: sx (ω)=s=cons t. Найдем корреляционную функцию белого шума. Используя формулу (**) (см. § 3)
получим
Приняв во внимание, что [см. § 6, соотношение (*)]
окончательно имеем
Таким образом, корреляционная функция стационарного белого шума пропорциональна дельта-функции; коэффициент пропорциональности 2πs называют интенсивностью стационарного белого шума. Дельта-функция равна нулю при всех значениях τ≠0, поэтому и корреляционная функция kx (τ) также равна нулю при этих же значениях τ [это видно из формулы (**)]. Равенство же нулю корреляционной функции стационарного белого шума означает некоррелированность любых двух его сечений—случайных величин Х (t 1) и Х (t2)(t 1≠ t 2).Благодаря этой особенности белый шум находит широкое применение в теории случайных функций и ее приложениях. Однако эта же особенность указывает на то, что осуществить белый шум невозможно, так как в действительности при очень близких значениях t 1 и t 2 соответствующие случайные величины Х (t 1) и Х (t 2) в известной степени коррелированы. Таким образом, стационарный белый шум—математическая абстракция, полезная для теории случайных функций и ее приложений. В частности, белый шум используют для моделирования случайных процессов, которые имеют постоянную спектральную плотность в определенном диапазоне частот, причем поведение спектральной плотности вне его исследователя не интересует. Пример. Спектральная плотность стационарной случайной функции Х (t) постоянна в диапазоне частот (- ω 0, ω 0). а вне его равна нулю:
Найти: а) корреляционную функцию; б) дисперсию случайнойфункции Х (t). Решение, а) Найдем искомую корреляционную функцию:
Итак,
б) Найдем искомую дисперсию:
Итак, Dx=2sω0.
§ 8. Преобразование стационарной случайной функции стационарной линейной динамической системой Стационарной линейной динамической системой называют устройство, которое описывается линейным дифференциальным уравнением с постоянными коэффициентами вида
где Х (t) — входная стационарная случайная функция (воздействие, возмущение), Y (t) — выходная случайная функция (реакция, отклик). Если динамическая система устойчива, то при достаточно больших значениях t, т. е. по окончании переходного процесса, функцию Y (t) можно считать стационарной. Подчеркнем, что при дальнейшем изложении предполагается, что X (t) и Y (t) — стационарные случайные функции. Поставим перед собой задачу найти характеристики выходной функции по известным характеристикам входной функции. Найдем математическое ожидание тy, зная тx, для чего приравняем математические ожидания левой и правой частей уравнения (*). Учитывая, что Х (t) и Y (t) — стационарные случайные функции, а значит, математические ожидания производных этих функций равны нулю, получим anmy=bmmx Отсюда искомое математическое ожидание my=bmmx/ an (**) Пример 1. На вход линейной динамической системы, описываемой уравнением Y ’(t)+ 2Y (t)=5 X ’(t)+6 X (t). подается стационарная случайная функция Х (t) с математическим ожиданием тx= 10. Найти математическое ожидание случайной функции Y (t) на выходе системы в установившемся режиме (после затухания переходного процесса). Решение. Используя формулу (**), получим my=bmmx/ an=(6/2)10=30. Введем понятия передаточной функции и частотной характеристики, которые понадобятся далее. Предварительно запишем уравнение (*) в операторной форме, обозначив оператор дифференцирования (a 0 pn+a 1 pn-l+... +an) Y (t) = (b 0 pm+b 1 pm-l+... +bm)X (t). (***) «Решим»это уравнение относительно Y (t):
Передаточной функцией линейной динамической системы называют отношение многочлена относительно р при Х (t)к многочлену при Y (t) в операторном уравнении (***):
Из соотношения (****) следует, что выходная и входная функции связаны равенством Y (t) = Ф(р) Х (t). Частотной характеристикой линейной динамической системы называют функцию, которая получается заменой аргумента р в передаточной функции на аргумент iω (ω —действительное число):
Доказано, что спектральные плотностивыходнойивходной функций связаны равенством sy (ω)= sx (ω)|Ф(iω)|2. Отсюда заключаем: для того чтобы найти спектральную плотность выходной функции, надо умножить спектральную плотность входной функции на квадрат модуля частотной характеристики. Зная же спектральную плотность выходной функции, можно найти ее корреляционную функцию [§ 3, формула (**)]:
а следовательно, и дисперсию:
Пример 2. На вход линейной стационарной динамической системы, описываемой уравнением 3 Y ’(t)+ Y (t)=4 X '(t)+X(t), подается стационарная случайная функция Х (t) с корреляционной функцией kx (τ) = 6 e-τ. Найти дисперсию случайной функции Y (t) на выходе системы в установившемся режиме. Решение 1. Найдем спектральную плотность выходной функции. Используя решение примера 2 (см. § 4) при D =6 и α=2, получим
2. Найдем передаточную функцию, длячего напишем заданное уравнение в операторной форме: (3 р +1)Y(t)=(4 р +1) Х (t). Отсюда
Следовательно, передаточная функция
3. Найдем частотную характеристику, для чего заменим в передаточной функции аргумент р на iω):
4. Найдем спектральную плотность выходной функции, длячегоумножим спектральную плотность входной функции на квадрат модуля частотной характеристики:
5. Найдем искомую дисперсию:
Представим подынтегральную функцию в виде суммы простейших дробей:
Выполнив интегрирование, получим искомую дисперсию: Dу= 96,4. Задачи 1. Найти дисперсию стационарной случайной функции X (t), зная ее спектральную плотность Отв. Dx=6. 2. Найти спектральную плотность стационарнойслучайнойфункции Х (t), знаяее корреляционную функцию
Отв. 3. Найти спектральную плотность стационарной случайной функции Х (t), зная ее корреляционную функцию kx (τ)=5e-2|τ|. Отв. sx (ω) = 10/(π (4 + ω 2)). 4. Задана спектральная плотность sx (ω)=6/(π (1+ ω 2)) стационарной случайной функции Х (t). Найти нормированную спектральную плотность. Отв. sxнорм(ω)=1/(π (1 – ω2)). 5. Найти корреляционную функцию стационарной случайной функции Х (t), зная ее спектральную плотность
Отв. 6. Спектральная плотность стационарной случайной функции X (t)постоянна в диапазоне частот (ω 1, ω 2), а вне его равна нулю:
Найти: а) корреляционную функцию; б) дисперсию; в) нормированную корреляционную функцию случайной функции Х (t). Отв. а) 7. На вход линейной стационарной динамической системы, описываемой уравнением Y' (t) + 3 Y (t) =X' (t) + 4 X(t),подается стационарная случайная функция Х (t)с математическим ожиданием mx =6 и корреляционной функцией kx (τ)=5e-2 τ. Найти математическое ожидание и дисперсию случайной функции Y (t) навыходе системы в установившемся режиме. Отв. my=8; Dy=22/3. 8. На вход линейной стационарной динамической системы, описываемой уравнением Y '(t) + 5 Y (t)+6 Y (t)=X’(t)+X(t), подается стационарная случайная функция X (t) с математическим ожиданием mх =4 и корреляционной функцией k x(t) =е-τ. Найти математическое ожидание и спектральную плотность случайной функции Y (t) на выходе системы в установившемся режиме. Отв. my =2/3; sy (ω)=1/[25π ω 2+(9= ω 2)2]. 9. На вход линейной стационарной динамической системы, описываемой уравнением Y ```(t)+6 Y ``(t)+11 Y `(t)+6 Y (t)=7 X "'(t)+5 X (t), подается стационарная случайная функция Х (t)с известной корреляционной функцией kx (τ)=2e-|τ|(1+|τ|). Найти спектральную плотность случайной функции Y (t) на выходе системы в установившемся режиме. Указание. Разложить на линейные множители знаменатель передаточной функции: р 3+б р 2+11 р +6=(р +1) (p +2)(p +3). Отв. sy(ω)=4(49 ω 6+25)/(π(ω 2+l)3(ω 2+4)(ω 2+9)). 10. На вход линейной стационарной динамической системы, описываемой уравнением Y' (t)+ Y (t)=(t), поступает случайная функция Х (t) с постоянной спектральной плотностью S0 (стационарный белый шум). Найти дисперсию случайной функции Y (t) на выходе системы в установившемся режиме. Отв. D = s 0 π.
ДОПОЛНЕНИЕ А. Пример расчета многоканальной системы
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.253.199 (0.012 с.) |



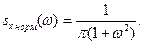
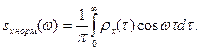

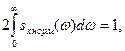 или
или 
 , равна единице.
, равна единице.
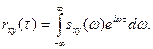
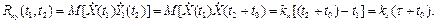
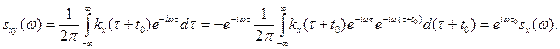


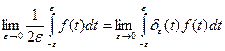 (ε>0),
(ε>0),
 условно пишут
условно пишут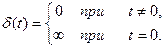


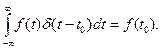
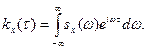

 (**)
(**)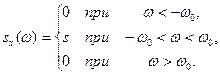



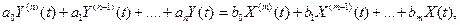
 через р,
через р, 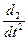 — через р 2 и т. д. В итоге уравнение (*) примет вид
— через р 2 и т. д. В итоге уравнение (*) примет вид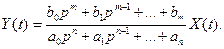 (****)
(****)

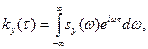
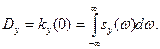

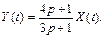
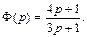
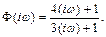

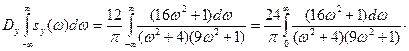

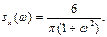

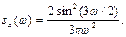

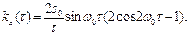
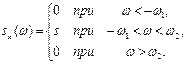
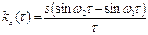 , б) Dx = s (ω2-ω1),в) ρx (τ)=
, б) Dx = s (ω2-ω1),в) ρx (τ)= 



