
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эмпирические и выравнивающие (теоретические) частотыСодержание книги
Поиск на нашем сайте
А. Дискретное распределение. Рассмотрим дискретную случайную величину X, закон распределения которой неизвестен. Пусть произведено п испытаний, в которых величина X приняла n 1раз значение х 1, n 2 раз значение x 2,.... nk раз значение xk, причем Эмпирическими частотами называют фактически наблюдаемые частоты ni. Пусть имеются основания предположить, что изучаемая величина X распределена по некоторому определенному закону. Чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, т. е. находят теоретически частоту ni' каждого из наблюдаемых значений в предположении, что величина X распределена по предполагаемому закону. Выравнивающими (теоретическими)в отличие от фактически наблюдаемых эмпирических частот называют частоты ni' найденные теоретически (вычислением). Выравнивающие частоты находят с помощью равенства ni' = nPi, где n — число испытаний; Рi — вероятность наблюдаемого значения хi, вычисленная при допущении, что X имеет предполагаемое распределение. Итак, выравнивающая частота наблюдаемого значения xi дискретного распределения равна произведению числа испытаний на вероятность этого наблюдаемого значения. Пример. В результате эксперимента, состоящего из n = 520 испытаний, в каждом из которых регистрировалось число хi появлений некоторого события, получено следующее эмпирическое распределение: набл. значения.. xi 0 1 2 34567 эмп. частота. ni 120 167 130 69 27 5 1 1 Найти выравнивающие частоты ni' в предположении, что случайная величина X (генеральная совокупность) распределена по закону Пуассона. Решение. Известно, что параметр λ, которым определяется распределение Пуассона, равен математическому ожиданию этого распределения. Поскольку в качестве оценки математического ожидания принимают выборочную среднюю (см. гл. XVI, § 5), то и в качестве оценки λможно принять выборочную среднюю Таким образом, формула Пуассона
принимает вид
Пользуясь этой формулой, найдем вероятности Р 520(К)при k = 0, 1, 2, 3, 4, 5, 6, 7 (для простоты записи индекс 520 далее опущен): Р (0) = 0,22313, Р (1) = 0,33469, Р (2) = 0,251 021, Р (3) = 0,125511, Р (4) = 0,047066, Р (5) = 0,014120, Р (6) = 0,003530, P (7) =0,000755. Найдем выравнивающие частоты (результаты умножения округлены до единицы): n 1 ' = n Р(0) = 520-0,22313 =116, n 2 ' = nP (1) = 520-0,33469= 174. Аналогично находят и остальные выравнивающие частоты. В итоге получим: эмп. частота.. 123 167 130 69 27 5 1 1 выр. частота.. 116 174 131 65 25 7 2 0 Сравнительно небольшое расхождение эмпирических и выравнивающих частот подтверждает предположение, что рассматриваемое распределение подчинено закону Пуассона. Заметим, что если подсчитать выборочную дисперсию по данному распределению, то окажется, что она равна выборочной средней, т.е. 1,5. Это служит еще одним подтверждением сделанного предположения, поскольку для распределения Пуассона λ = М (X) = D (X) Сравнения эмпирических и теоретических частот сна глаз», конечно, недостаточно. Чтобы сделать это более обоснованно, надо использовать, например, критерий Пирсона (см. гл. XIX, § 23). Проверка гипотезы о распределении случайной величины по закону Пуассона изложена в книге: Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М., «Высшая школа», 1972 (см. гл. XIII, § 17). Б. Непрерывное распределение. В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю (см. гл, X, § 2, следствие 2). Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности Pi попадания X в i -й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности. Итак, выравнивающие частоты непрерывного распределения находят по равенству ni'=nPi, где п — число испытаний; Рi — вероятность попадания X в i -й частичный интервал, вычисленная при допущении, что X имеет предполагаемое распределение. В частности, если имеются основания предположить, что случайная величина X (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле
где п — число испытаний (объем выборки), h — длина частичного интервала, σв — выборочное среднее квадрати-ческое отклонение,
Пример на применение формулы (*) приведен в § 7. Пояснение. Поясним происхождение формулы (*). Напишем плотность общего нормального распределения:
При а = 0 и σ = 1 получим плотность нормированного распределения:
или, изменив обозначение аргумента,
Положив и = (х - а) /σ, имеем
Сравнивая (**) и (***), заключаем, что
Если математическое ожидание а и среднее квадратическое отклонение σ неизвестны, то в качестве оценок этих параметров принимают соответственно выборочную среднюю
где Пусть xi- середина i -гo интервала (на которые разбита совокупность всех наблюдаемых значений нормально распределенной случайной величины X)длиной h. Тогда вероятность попадания X в этот интервал приближенно равна произведению длины интервала на значение плотности распределения f (x)в любой точке интервала и, в частности, при х=xi (см. гл. XI, § 5):
Следовательно, выравнивающая частота
где
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.183 (0.006 с.) |

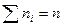 .
.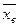 . Легко найти по условию, что выборочная средняя равна 1,5, следовательно, можно принять λ =1,5.
. Легко найти по условию, что выборочная средняя равна 1,5, следовательно, можно принять λ =1,5.

 , (*)
, (*)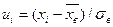 (xi — середина i -гo частичного интервала),
(xi — середина i -гo частичного интервала), .
. . (**)
. (**)
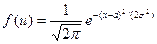 (***)
(***)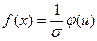 .
. ,
,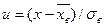 .
. .
.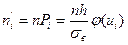 ,
,


