
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показательный закон надежностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часто длительность времени безотказной работы момента имеет показательное распределение, функция распределения которого F (t) = 1- Следовательно, в силу соотношения (*) предыдущего параграфа функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид R (t) = 1 — F (t) = 1 — (1 — Показательным законом надежности называют функциюнадежности, определяемую равенством R (t) = где l— интенсивность отказов. Как следует из определения функции надежности (см. § 4), эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью t, если время безотказной работы имеет, показательное, распределение. Пример. Время безотказной работы элемента распределено по показательному закону f (t) =0,02 e- 0, 02 t при t Решение. По условию, постоянная интенсивность отказов l=0,02. Воспользуемся формулой (*): R (100) = е- 0, 02 * 100 =е- 2 = 0, 13534. Искомая вероятность того, что элемент проработает безотказно 100 ч, приближенно равна 0,14. Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за времядлительностью t не наступит ни одного отказа (см. гл. VI, § 6), Pt (0) = чтосогласуется с равенством (*), поскольку l в обеих формулах имеет один и тот же смысл (постоянная интенсивность отказов). Характеристическое свойство показательного закона надежности
Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивности отказов l). Для доказательства свойства введем обозначения событий: А —безотказная работа элемента на интервале (О, t 0) длительностью t 0; В —безотказная работа на интервале (t 0, t 0 +t) длительностью t. Тогда АВ —безотказная работа на интервале (0, t 0 +t)длительностью to +t. Найдем вероятности этих событий по формуле (*) (см. § 5): P (A) = P (AB) = Найдем условную вероятность того, что элемент будет работать безотказно на интервале (t 0, t 0 +t)при условии, что он уже проработал безотказно на предшествующем интервале (0, t 0)(см. гл. III, § 2):
Полученная формула не содержит t 0, а содержит только t. Это и означает, что время работы на предшествующем интервале не сказывается на величине вероятности безотказной работы на последующем интервале, а зависит только от длины последующего интервала, что и требовалось доказать. Полученный результат можно сформулировать несколько иначе. Сравнив вероятности Р (В)= Итак, вслучае показательного закона надежности безотказная работа элемента «в прошлом» не сказывается на величине вероятности его безотказной работы «в ближайшем будущем». Замечание. Можно доказать, что рассматриваемым свойством обладает только показательное распределение. Поэтому если на практике изучаемая случайная величина этим свойством обладает, то она распределена по показательному закону. Например, при допущении, что метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попадали или не попадали метеориты в корабль до начала рассматриваемого интервала времени. Следовательно, случайные моменты времени попадания метеоритов в космический корабль распределены по показательному закону. Задачи 1. Написать функцию распределения F (х)и плотность вероятности f (к)непрерывной случайной величины X, распределенной по показательному закону с параметром l = 5. Отв. f (х) = 5 е- 5 x при x 2. Непрерывная случайная величина X распределена по показательному закону: f (х) = 5 е- 5 x при х Отв. Р (0,4 < X < 1)=0,13. 3. Непрерывная случайная величина X распределена по показательному закону f (х) = 4 е- 4 x (х > 0). Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X. Отв. М (Х) = s(Х) = 0, 25; D (X) = 0,0625. 4. Время безотказной работы элемента распределено по показательному закону f (t) = 0, 01 e- 0, 01 t (t> 0), где t — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч. Отв. R (100) = 0,37.
До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости,- дискретная одномерная величина; расстояние от орудия до места падения снаряда - непрерывная одномерная случайная величина. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, …, п числами. Такие величины называются соответственно двумерными, трехмерными,..., n-мерными. Будем обозначать через (X, Y)двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему п случайных величин. Например, трехмерная величина (X, Y, Z)определяет систему трех случайных величин X, Y и Z. Пример. Станок-автомат штампует стальные плитки. Если контролируемыми размерами являются длина X и ширина Y, то имеем двумерную случайную величину (X, Y); если же контролируется и высота 2, то имеем трехмерную величину (X, Y, Z). Двумерную случайную величину (X, Y)геометрически можно истолковать либо как случайную точку М (X, Y)на плоскости (т. е. как точку со случайными координатами), либо как случайный вектор ОМ. Трехмерную случайную величину геометрически можно истолковать как точку М (X, Y, Z) в трехмерном пространстве или как вектор OM. Целесообразно различать дискретные (составляющие этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) многомерные случайные величины.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.01 с.) |

 .
. 0 (t — время). Найти вероятность того, что элемент проработает безотказно 100 ч.
0 (t — время). Найти вероятность того, что элемент проработает безотказно 100 ч. ,P (B) =
,P (B) = 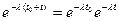 .
.



