
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вычисления выборочного коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть требуется по данным корреляционной таблицы вычислить выборочный коэффициент корреляции. Можно значительно упростить расчет, если перейти к условным вариантам (при этом величина rв не изменится) ui=(xi—С1)/h1 и υj=:(yj—С2)/h2. В этом случае выборочный коэффициент корреляции вычисляют по формуле
Величины u, υ Можно доказать, что справедливы формулы (см. пояснение в конце параграфа):
Для контроля целесообразно выполнить расчеты по обеим формулам и сравнить результаты; их совпадение свидетельствует о правильности вычислений. Покажем на примере, как пользоваться приведенными формулами. Пример 1. Вычислить ^ "по"" П0 данным корреляционной табл. 14.
Таблица 14
Решение. Перейдем к условным вариантам: ui=(xi—С1)/h1 = = (xi —40)/10 (в качестве ложного нуля С1 взята варианта х=40. расположенная примерно в середине вариационного ряда; шаг h1 равен разности между двумя соседними вариантами: 20—10 = 10) и υj=:(yj—С2)/h2 = (yj —35)/10 (в качестве ложного нуля С2 взята варианта у =35, расположенная в середине вариационного ряда; шаг h2 равен разности между двумя соседними вариантами: 25—15=10). Составим корреляционную таблицу в условных вариантах. Практически это делают так: в первом столбце вместо ложного нуля С2 (варианты 35) пишут 0; над нулем последовательно записывают —1, —2; под нулем пишут 1, 2. В первой строке вместо ложного нуля С1 (варианты 40) пишут 0; слева от нуля последовательно записывают —1, —2, —3; справа от нуля пишут 1, 2. Все остальные данные переписывают из первоначальной корреляционной таблицы. В итоге получим корреляционную табл. 15 в условных вариантах.
Таблица 15
Теперь для вычисления искомой суммы 1. В каждой клетке, в которой частота nuυ ≠ 0, записывают в правом верхнем углу произведение частоты nuυ на варианту u. Например, в правых верхних углах клеток первой строки записаны произведения: 5·(—3) = —15; 7·(—2) = —14. 2. Складывают все числа, помещенные в правых верхних углах клеток одной строки и их сумму записывают в клетку этой же строки столбца u. Например, для первой строки U == —15+(—14)= —29. 3. Умножают варианту υ на U и полученное произведение заци-сывают в последнюю клетку той же строки, т. е. в клетку столбца υU. Например, в первой строке таблицы υ = —2, U = —29; следовательно, υU = (—2)·(—29) = 58. 4. Наконец, сложив все числа столбца υU, получают сумму
Таблица 16
Для контроля аналогичные вычисления производят по столбцам: произведения nuυυ записывают в левый нижний угол клетки, содержащей частоту nuυυ ≠ 0; все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму записывают в строку V; далее умножают каждую варианту u на V и результат записывают в клетках последней строки. Наконец, сложив все числа последней строки, получают сумму Теперь, когда мы научились вычислять Пример на отыскание выборочного уравнения прямой линии регрессии Теперь, когда известно, как вычисляют rв, уместно привести пример на отыскание уравнения прямой линии регрессии. Поскольку при нахождении rв уже вычислены
Здесь сохранены обозначения предыдущего параграфа. Рекомендуем читателю самостоятельно вывести эти формулы. Пример. Найти выборочное уравнение прямой линии регрессии Y на Х по данным корреляционной табл. 14 примера предыдущего параграфа. Решение. Напишем искомое уравнение в общем виде:
Коэффициент корреляции уже вычислен в предыдущем параграфе. Остается найти
или окончательно
Сравним условные средние, вычисленные: а) по этому уравнению; б) по данным корреляционной табл. 14. Например, при х =30: а) б) Как видим, согласование расчетного и наблюдаемого условных средних—удовлетворительное. Предварительные соображения к введению меры любой корреляционной связи Выше рассматривалась оценка тесноты линейной корреляционной связи. Как оценить тесноту любой корреляционной связи? Пусть данные наблюдений над количественными признаками Х и Y сведены в корреляционную таблицу. Можно считать, что тем самым наблюдаемые значения Y разбиты на группы; каждая группа содержит те значения Y, которые соответствуют определенному значению X. Например, дана корреляционная табл. 17. К первой группе относятся те 10 значений Y (4 раза наблюдалось y1=3 и 6 раз y2 = 5), которые соответствуют x1=8. Ко второй группе относятся те 20 значений Y (13 раз наблюдалось у1 = 3 и 7 раз y2 = 5), которые соответствуют x2 = 9. Таблица 17
Условные средние теперь можно назвать групповыми средними: групповая средняя первой группы Поскольку все значения признака Y разбиты на группы, можно представить общую дисперсию признака в виде суммы внутригрупповой и межгрупповой дисперсий (см. гл. XVI, § 12): Dобщ = Dвнгр + Dмежгр. (*) Покажем справедливость следующих утверждений: 1) если Y связан с Х функциональной зависимостью, то Dмежгр/Dобщ = 1; 2) если Y связан с X корреляционной зависимостью, Dмежгр/Dобщ < 1.
Доказательство. 1) Если Y связан с Х функциональной зависимостью, то определенному значению Х соответствует одно значение Y. В этом случае в каждой группе содержатся равные между собой значения Y поэтому групповая дисперсия каждой группы равна нулю. Следовательно, средняя арифметическая групповых дисперсий (взвешенная по объемам групп), т. е. внутригрупповая дисперсия Dвнгр = 0 и равенство (*), имеет вид
Dобщ = Dмежгр. Отсюда Dмежгр /Dобщ= 1.
2) Если Y связан с Х корреляционной зависимостью, то определенному значению Х соответствуют, вообще говоря, различные значения Y (образующие группу). В этом случае групповая дисперсия каждой группы отлична от нуля. Следовательно, средняя арифметическая групповых дисперсий (взвешенная по объемам групп) Dвнгр ≠ 0. Тогда одно положительное слагаемое Dмежгр меньше суммы двух положительных слагаемых Dвнгр + Dмежгр = Dобщ.
Dмежгр < Dобщ Отсюда Dмежгр /Dобщ< 1 Уже из приведенных рассуждений видно, что чем связь между признаками ближе к функциональной, тем меньше Dвнгр и, следовательно, тем больше приближается Dмежгр к Dобщ, а значит, отношение Dмежгр /Dобщ — к единице. Отсюда ясно, что целесообразно рассматривать в качестве меры тесноты корреляционной зависимости отношение межгрупповой дисперсии к общей, или, что то же, отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 738; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.01 с.) |

 .
.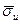 и
и  можно найти методом произведений (см. гл. XVII, § 4), а при малом числе данных— непосредственно исходя из определений этих величин. Остается указать способ вычисления
можно найти методом произведений (см. гл. XVII, § 4), а при малом числе данных— непосредственно исходя из определений этих величин. Остается указать способ вычисления  , где
, где  — частота пары условных вариант (u, υ).
— частота пары условных вариант (u, υ).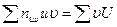 , где
, где  ,
, , где
, где  .
. , которая равна искомой сумме
, которая равна искомой сумме 
 ==169
==169
 ,
, 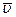 ,
,  ,
,  =h1
=h1  =h2
=h2 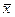 =
= 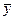 =
=  (*)
(*) ,
, = 0,659x + 12,34.
= 0,659x + 12,34. ==0,659·30+12,34 = 32,11;
==0,659·30+12,34 = 32,11; = (4·3+6·5)/10==4,2; групповая средняя второй группы
= (4·3+6·5)/10==4,2; групповая средняя второй группы  =(13·3+7·5)/20=3,7.
=(13·3+7·5)/20=3,7.


