
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность гипотез. Формулы БейесаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности (см. § 2): Р (А) = Р (В 1) Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности РА (В 1), РА (В 2) ,..., РА (Вп). Найдем сначала условную вероятность Pa (B 1).По теореме умножения имеем Р (АВ 1) = Р (А) РА (В 1) = Р (B 1) Отсюда РА (В 1) = Заменив здесь Р (А)по формуле (*), получим РА (В 1) = Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы Bi (i= 1, 2 ,..., п)может быть вычислена по формуле РА (Вi) = Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым—0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения: 1)деталь проверил первый контролер (гипотеза B 1); 2)деталь проверил второй контролер (гипотеза В 2). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса: РА (В 1) = По условию задачи имеем: Р (В 1) = 0, 6(вероятность того, что деталь попадает к первому контролеру); P (В 2) = 0,4 (вероятность того, что деталь попадет ко второму контролеру);
Искомая вероятность РА (В 1) = (0, 6 * 0, 94) / (0, 6 * 0, 94 + 0, 4 * 0, 98) Как видно, до испытания вероятность гипотезы В 1равнялась 0,6, после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.
Задачи 1. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым—0,5. Найти вероятность того, что хотя бы один из стрелков попал и мишень. Отв. 0,88. 2. У сборщика имеется 16 деталей, изготовленных заводом № 1, и 4 детали завода № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1. Отв. 92/95. 3. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника—0,9, для велосипедиста—0,8. и для бегуна—0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. Отв. 0,86. 4. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 — 0,9, Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь. Отв. 0,84. 5. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором—30 деталей, из них 24 стандартных; в третьем — 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика—стандартная. Отв. 43/60. 6. В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы. Отв. 0,875. 7. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.
Отв. 13/132. 8. Из полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую извлеченную наудачу кость можно приставить к первой. Отв. 7/18. 9. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей: когда он берет билет первым или последним? Отв. Вероятности одинаковы в обоих случаях. 10. В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартныхдеталей, первоначально находящихся в ящике. Отв. 0,625. 11. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11, соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11? Отв. Вероятность того, что автомат снабжен сигнализатором С-1, равна 6/11, а С-11— 5/11 12. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй — 6, из третьей группы — 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент? Отв. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59. 13. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту,— с вероятностью 0,05. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту. Отв. 0, 998. Глава пятая ПОВТОРЕНИЕ ИСПЫТАНИЙ Формула Бернулли Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность. Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q= 1 — p. Поставим перед собой задачу вычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п — k раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно к раз в определенной последовательности. Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: ААА
Искомую вероятность обозначим Pn (k). Например, символ P 5(3) означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза. Поставленную задачу можно решить с помощью так называемой формулы Бернулли. Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п — k раз, по теореме умножения вероятностей независимых событий равна pkqn-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из п элементов по k элементов, т. е. Pn (k) = или Pn (k) = Полученную формулу называют формулой Бернулли. Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р =0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы. Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q= 1 -p= 1 — 0, 75 = 0, 25. Искомая вероятность по формуле Бернулли равна P 6(4) = Локальная теорема Лапласа
Выше была выведена формула Бернулли, позволяющая вычислить вероятность того, что событие появится в n испытаниях ровно k раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях п достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если п = 50, k = 30, p= 0,1, то для отыскания вероятности Р 50(30) надо иычислить выражение Р 50(30)=50!/(30!20!)*(0,1)30*(0,9)20,где 50!=30414 093*1057, 30!=26525286*1025, 20!=24329020*1011. Правда, можно несколько упростить исчисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицысодержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного.
Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает асимптотическую (Функцию f (x)называют асимптотическим приближением функции f (x), если Заметим, что для частного случая, а именно для p= 1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра — Лапласа. Доказательство локальной теоремы Лапласа довольно cложно, поэтому мы приведем лишь формулировку теоремы и примеры, иллюстрирующие ее использование. Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции y= при x= (k-np) / Имеются таблицы, в которых помещены значения функции
Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна Pn (k) где x = (k — np) / Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение. По условию, п = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: Р 400(80) Вычислим определяемое данными задачи значение х: x= (k- пр) / По таблице приложения 1 находим Искомая вероятность P 400(80) = (1 / 8) • 0, 3989 = 0, 04986. Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены): P 400(80) = 0, 0498. Пример 2. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз. Решение. По условию, n = 10; k = 8; р = 0, 75; q = 0,25. Воспользуемся асимптотической формулой Лапласа: Р 10(8) Вычислим определяемое данными задачи значение х: x= По таблице приложения 1 находим Искомая вероятность Р 10(8) = 0,7301.0,3739 = 0,273. Формула Бернулли приводит к иному результату, а именно P 10(8) =0,282. Столь значительное расхождение ответов объясняетсятем, что в настоящем примере п имеет малое значение ( формулаЛапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п)
.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.43 (0.016 с.) |

 (А) + Р (В 2)
(А) + Р (В 2)  (А) +...+ Р (Вn)
(А) +...+ Р (Вn)  (А). (*)
(А). (*)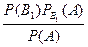 .
.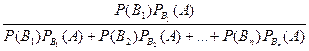 .
. .
. .
. 0, 59.
0, 59. , АА
, АА  . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в п испытаниях) равна вероятности одного сложного события, умноженной на их число:
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в п испытаниях) равна вероятности одного сложного события, умноженной на их число: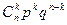
 .
. p 4 q 2 =
p 4 q 2 = 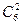 p 4 q 2 =
p 4 q 2 =  (0, 75)4 * (0, 25)2 = 0, 30.
(0, 75)4 * (0, 25)2 = 0, 30. ) формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико.
) формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико.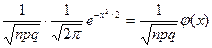
 .
. (х) =
(х) =  , соответствующие положительным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция
, соответствующие положительным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 


 ,
,



