
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 5. Формула полной вероятности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Краткая теоретическая часть Предположим, что событие В может осуществиться с одним и только с одним из n несовместимых событий Применяя теорему умножения, находим:
Это равенство носит название формулы полной вероятности и играет важную роль во всей дальнейшей теории. Тест. 1. Пусть а) б) в) г) д) Событие е) Событие ж) Событие
2. Что означает тот факт, что а) б) в)
3. Какие из следующих групп событий а) б) в) г) д)
4. Какой вид имеет формула полной вероятности? а) б) в) г) Решение типовых задач Пример 5.1. Среди n лиц разыгрываются т
Решение. Обозначим через Ak событие, состоящее в извлечении выигрышного билета после k извлечений билетов из ящика. По результатам предыдущих опытов можно сделать k+ 1 гипотез. Пусть гипотеза Hks означает, что из k извлеченных билетов выигрышных было s. Вероятности этих гипотез
причем
Так как осталось n—k билетов, из которых т—s выигрышных, то при m
По формуле полной вероятности находим
где Данное равенство можно записать также в виде
Имеем
т. е. справедливо равенство
Искомая вероятность Р(Ak)=
Пример 5.2. Отмеченный шар с вероятностями p и 1— p может находиться в первой или во второй урне. Вероятность извлечь отмеченный шар из урны, в которой этот шар находится, равна Р(Р
Решение. Пусть событие А — извлечение отмеченного шара. Гипотезы: H1— шар находится в первой урне, H2— во второй. По условию P(H1)=p, Р(H2)= 1 —р. Допустим, что из первой урны извлечено т, а из второй n — т шаров. Условные вероятности извлечения отмеченного шара будут
По формуле полной вероятности искомая вероятность
Нужно определить т так, чтобы была наибольшей вероятность Р (А). Дифференцируя Р(A) по т (для нахождения приближенного значения т считаем m непрерывным), получаем
Полагая,
Поэтому должно быть
5.4. Задачи для самостоятельной работы 5.1. Имеются две партии изделий по 12 и 10 штук, причем в каждой партии одно изделие бракованное. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии. (Ответ: p =
5.2. Из полного набора костей домино наугад берутся две кости. Определить вероятность того, что вторую кость можно приставить к первой. (Ответ: p =
5.3. Имеется n урн, в каждой из которых по m белых и по k черных шаров. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны наудачу извлекается один шар и перекладывается в третью урну и т. д. Определить вероятность извлечения после такого перекладывания белого шара из последней урны. (Ответ: p =
5.4. В тире имеются пять ружей, вероятности попадания из которых равны соответственно 0,5; 0,6; 0,7; 0,8 и 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу. (Ответ: p = 0,7)
5.5. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии (Ответ: p =
5.6. Характеристика материала, взятого для изготовления продукции, с вероятностями 0,09; 0,16; 0,25; 0,25; 0,16 и 0,09 может находиться в шести различных интервалах. В зависимости от свойств материала вероятности получения первосортной продукции равны соответственно 0,2; 0,3; 0,4; 0,4; 0,3 и 0,2. Определить вероятность получения первосортной продукции. (Ответ: p = 0,332)
5.7. В сосуд, содержащий n шаров, опущен белый шар. Какова вероятность извлечь из этого сосуда белый шар, если все предположения о первоначальном числе белых шаров равновозможны? (Ответ: p =
5.8. В ящике находятся 15 теннисных мячей, из которых 9 новых. Для первой игры наугад берутся три мяча, которые после игры возвращаются в ящик. Для второй игры также наугад берутся три мяча. Найти вероятность того, что все мячи, взятые для второй игры, новые. (Ответ: p = 0,089)
5.9. В правом кармане имеются три монеты по 20 коп. и четыре монеты по 3 коп., а в левом — шесть по 20 коп. и три по 3 коп. Из правого кармана в левый наудачу перекладываются пять монет. Определить вероятность извлечения из левого кармана после перекладывания монеты в 20 коп, если монета берется наудачу. (Ответ: p =
5.10. Пятнадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на указанный дополнительный вопрос из другого билета. (Ответ: p = Занятие 6. Формула Бейеса. Краткая теоретическая часть Получим важные формулы Бейеса или, как иногда говорят, формулы вероятности гипотез. Требуется найти вероятность события Ai, если известно, что В произошло. Согласно теореме умножения имеем:
Из соотношения (6.1) получаем
Используя формулу полной вероятности (5.1), находим:
Полученные формулы (6.3) носят название формул Бейеса. Общая схема применения этих формул к решению практических задач такова. Пусть событие В может протекать в различных условиях, относительно характера которых может быть сделано n гипотез: Вероятности Тест 1. При решении каких задач следует применить формулу Бейеса? а) Найти вероятность события В, которое зависит от гипотез б) Найти вероятность справедливости гипотезы в) Найти апостериорную вероятность гипотезы г) Найти априорную вероятность гипотезы д) Найти вероятность справедливости гипотезы
2. Какие условия должны накладываться на событие В и гипотезы а) Гипотезы б) Гипотезы в) Событие В может протекать в различных условиях, относительно характера которых может быть сделано n гипотез г) Событие В может протекать в различных условиях, относительно характера которых не может быть сделана ни одна из n гипотез
3. Какой вид имеет формула Бейеса? а) б) в)
4. Как называются вероятности а) Априорные вероятности события б) Апостериорные вероятности события Решение типовых задач Пример 6.1. Телеграфное сообщение состоит из сигналов «точка» и «тире». Статистические свойства помех таковы, что искажаются в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в отношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если: а) принят сигнал «точка»; б) принят сигнал «тире».
Решение. Пусть событие А —принят сигнал «точка», а событие В — принят сигнал «тире». Можно сделать две гипотезы: Н1 — передан сигнал «точка», Н2 — передан сигнал «тире». По условию Р(Н1):Р(Н2) = 5:3. Кроме того, P(Н1) + P(Н2) = l. Поэтому P(Н1) = Известно, что
Вероятности событий A и В находим по формуле полной вероятности:
Искомые вероятности будут:
Пример 6.2. Имеется две партии деталей, причем известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии 1/4 деталей недоброкачественные. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что вторая деталь из этой же партии окажется недоброкачественной, если первая деталь после проверки возвращена в партию.
Решение. Введем событие А, состоящее в том, что первая деталь доброкачественная. Гипотезы: H1 — взята партия с недоброкачественными деталями, H2 — взята партия доброкачественных деталей. По условию задачи Р(H1) = Р(H2) = Р (A | H1) = Р (A | H2) = 1. Поэтому по формуле полной вероятности вероятность события А будет
После первого испытания вероятность того, что партия содержит недоброкачественные детали, равна
Вероятность того, что партия содержит только доброкачественные детали,
Пусть событие В состоит в том, что при втором испытании деталь оказалась недоброкачественной. Вероятность данного события также находится по формуле полной вероятности. Если
Кроме того,
Поэтому искомая вероятность
6.4. Задачи для самостоятельной работы 6.1. Имеется десять одинаковых урн, из которых в девяти находятся по два черных и по два белых шара, а в одной— пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность, что шар извлечен из урны, содержащей пять белых шаров? (Ответ: p =
6.2. Известно, что 96°/о выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную — с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту. (Ответ: p = 0,998)
6.3. Из партии в пять изделий наудачу взято одно изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно? (Ответ: Пять бракованных изделий)
6.4. Игрок D играет с неизвестным противником на следующих условиях: ничейный исход исключен; первый ход делает противник; в случае его проигрыша делает ход D, выигрыш которого означает выигрыш игры, а при проигрыше игра повторяется второй раз на тех же условиях. Из двух равновозможных противников В имеет вероятность выиграть первым ходом 0,4, а вторым — 0,3; С имеет вероятность выиграть первым ходом 0,8, а вторым ходом 0,6. Для D вероятность выиграть первым ходом равна 0,3 и не зависит от противника, а для второго хода равна 0,5 при игре с В и 0,7 при игре с C. Игру выиграл D. Какова вероятность: а) что противником был В; б) что противником был С? (Ответ: а) p =0,59; б) p = 0,41)
6.5. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 — с вероятностью 0,7; 4 — с вероятностью 0,6 и 2 — с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок? (Ответ: Ко второй группе)
6.6. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно (Ответ: p =
6.7. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятности того, что вепрь убит первым, вторым или третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6. (Ответ:
6.8. Два стрелка поочередно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0,4 и 0,5, а вероятности попадания при последующих выстрелах для каждого увеличиваются на 0,05. Какова вероятность, что первым произвел выстрел первый стрелок, если при пятом выстреле произошло попадание в мишень? (Ответ: p =
6.9. Произведено три независимых испытания, в каждом из которых событие A происходит с вероятностью 0,2. Вероятность появления другого события В зависит от числа появлений события A: при однократном появлении события A эта вероятность равна 0,1, при двукратном появлении равна 0,3, при трехкратном появлении равна 0,7; если событие A не имело места ни разу, то событие В невозможно. Определить наивероятнейшее число появлений события A, если событие В имело место. (Ответ: Одно появление)
6.10. Получена партия из восьми изделий одного образца. По данным проверки половины партии, три изделия оказались технически исправными, а одно бракованным. Какова вероятность, что при проверке трех последующих изделий одно из них окажется исправным, а два бракованными, если любое количество бракованных изделий в данной партии равновозможно? (Ответ: p =
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

 . Иными словами, положим
. Иными словами, положим  , где события BAi и BAj с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем:
, где события BAi и BAj с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем:  .
. (5.1)
(5.1) - некоторые события. Укажите 2 условия, при которых необходимо применить формулу полной вероятности для определения вероятности появления события
- некоторые события. Укажите 2 условия, при которых необходимо применить формулу полной вероятности для определения вероятности появления события  :
:
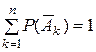

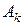 ,
,  не являются полными группами несовместных событий?
не являются полными группами несовместных событий? - извлечение шара из
- извлечение шара из  -той урны, содержащей
-той урны, содержащей  белых и
белых и  черных шаров, если шар извлекается наудачу из любой из
черных шаров, если шар извлекается наудачу из любой из  урн
урн -той урны, содержащей
-той урны, содержащей  белых и
белых и 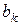 черных шаров, если шар извлекается наудачу из любых двух урн
черных шаров, если шар извлекается наудачу из любых двух урн



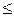 n выигрышей путем случайного извлечения из ящика n билетов. Одинаковы ли шансы выигрыша для любого из играющих? Когда выгоднее тащить билет?
n выигрышей путем случайного извлечения из ящика n билетов. Одинаковы ли шансы выигрыша для любого из играющих? Когда выгоднее тащить билет?
 .
. s
s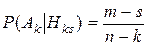 .
. ,
, при s>m.
при s>m. .
. ,
, .
. при любом k. Таким образом, у всех играющих шансы одинаковы и очередность извлечения не имеет значения.
при любом k. Таким образом, у всех играющих шансы одинаковы и очередность извлечения не имеет значения. 1). Как следует распорядиться правом n раз извлекать шары из любой урны, чтобы вероятность извлечения отмеченного шара хотя бы один раз была наибольшей, если шар после извлечения возвращается в урну?
1). Как следует распорядиться правом n раз извлекать шары из любой урны, чтобы вероятность извлечения отмеченного шара хотя бы один раз была наибольшей, если шар после извлечения возвращается в урну? .
. .
. .
. приходим к равенству
приходим к равенству .
.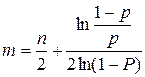 .
. )
)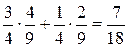 )
) )
) деталей бракованные, а в двух других — все доброкачественные?
деталей бракованные, а в двух других — все доброкачественные? )
) )
) )
) ).
).


 . По тем или иным причинам нам известны вероятности
. По тем или иным причинам нам известны вероятности  этих гипотез до испытания (априорные вероятности гипотез). Известно также, что гипотеза
этих гипотез до испытания (априорные вероятности гипотез). Известно также, что гипотеза  сообщает событию
сообщает событию  . Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез
. Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез  называются апостериорными вероятностями события
называются апостериорными вероятностями события  .
.
 при условии, что связанное с ней событие В произошло
при условии, что связанное с ней событие В произошло


 ?
?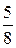 , P(Н2) =
, P(Н2) =  .
.


 ,
, ,
, .
.

 и
и  — вероятности гипотез H1 и H2 после испытания, то согласно предыдущим вычислениям
— вероятности гипотез H1 и H2 после испытания, то согласно предыдущим вычислениям ,
,  .
. ,
, .
.
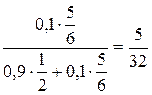 )
) . При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.
. При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок. )
) = 0,103;
= 0,103;  = 0,620)
= 0,620) )
) ).
).


