
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики функций случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим следующую задачу: случайная величина Y есть функция нескольких случайных величин
Пусть нам известен закон распределения системы аргументов Представим себе, что нам удалось найти закон распределения g (у) величины Y. Тогда задача об определении числовых характеристик становится простой; они находятся по формулам:
Однако задача нахождения закона распределения g(y) величины Y часто оказывается довольно сложной. Для решения поставленной задачи нахождение закона распределения величины Y не нужно: чтобы найти только числовые характеристики величины Y, нет надобности знать ее закон распределения; достаточно знать закон распределения аргументов Таким образом, возникает задача определения числовых характеристик функций случайных величин, не определяя законов распределения этих функций. Рассмотрим задачу об определении числовых характеристик функции при заданном законе распределения аргументов. Начнем с самого простого случая — функции одного аргумента. Имеется случайная величина X с заданным законом распределения; другая случайная величина Y связана с X функциональной зависимостью: Y= Требуется, не находя закона распределения величины Y, определить ее математическое ожидание:
Рассмотрим сначала случай, когда X есть дискретная случайная величина с рядом распределения: Табл. 6.7.1
Запишем в виде таблицы возможные значения величины Y и вероятности этих значений: Табл. 6.7.2
Таблица 6.7.2 не является рядом распределения величины Y, так как в общем случае некоторые из значений
могут совпадать между собой. Для того чтобы от таблицы (6.7.1) перейти к подлинному ряду распределения величины Y, нужно было бы расположить значения (6.7.5) в порядке возрастания, объединить столбцы, соответствующие равным между собой значениям Y, и сложить соответствующие вероятности. Математическое ожидание величины Y можно определить по формуле
Очевидно, величина ту — М( В формуле (6.7.6) для математического ожидания функции не содержится в явном виде закона распределения самой функции, а содержится только закон распределения аргумента. Таким образом, для определения математического ожидания функции вовсе не требуется знать закон распределения этой функции, а достаточно знать закон распределения аргумента. Заменяя в формуле (6.7.6) сумму интегралом, а вероятность рi — элементом вероятности, получим аналогичную формулу для непрерывной случайной величины:
где f(x) — плотность распределения величины X. Аналогично может быть определено математическое ожидание функции у(Х,Y) от двух случайных аргументов X и Y. Для дискретных величин
где
где f (x, у)— плотность распределения системы (X, Y). Аналогично определяется математическое ожидание функции от произвольного числа случайных аргументов. Приведем соответствующую формулу только для непрерывных величин:
где Формулы типа (6.7.10) весьма часто встречаются в практическом применении теории вероятностей, когда речь идет об осреднении каких-либо величин, зависящих от ряда случайных аргументов. Таким образом, математическое ожидание функции любого числа случайных аргументов может быть найдено помимо закона распределения функции. Аналогично могут быть найдены и другие числовые характеристики функции — моменты различных порядков. Так как каждый момент представляет собой математическое ожидание некоторой функции исследуемой случайной величины, то вычисление любого момента может быть осуществлено приемами, совершенно аналогичными вышеизложенным. Здесь мы приведем расчетные формулы только для дисперсии, причем лишь для случая непрерывных случайных аргументов. Дисперсия функции одного случайного аргумента выражается формулой
где т=М [ Аналогично выражается дисперсия функции двух случайных аргументов:
где
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.110.113 (0.006 с.) |

 ;
;

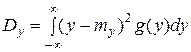
 (Х).
(Х).




 — вероятность того, что система (X,Y)примет значения (xi yj). Для непрерывных величин
— вероятность того, что система (X,Y)примет значения (xi yj). Для непрерывных величин

 — плотность распределения системы
— плотность распределения системы 

 — математическое ожидание функции
— математическое ожидание функции  (Х,Y); f(x, у) — плотность распределения системы (X,Y). Наконец, в случае произвольного числа случайных аргументов, в аналогичных обозначениях:
(Х,Y); f(x, у) — плотность распределения системы (X,Y). Наконец, в случае произвольного числа случайных аргументов, в аналогичных обозначениях:



