
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство. Рассмотрим величинуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Применим к величине Y неравенство Чебышева:
Так как по условию теоремы при
или, переходя к противоположному событию,
что и требовалось доказать. Следствия закона больших чисел. Пусть производиться n независимых опытов в каждом из которых с вероятностью p может произойти событие A, пусть Теорема Бернулли. При неограниченном увеличении числа опытов
Доказательство. Введем в рассмотрение независимые случайные величины
Тогда
Так как Предельная теорема Пуассона. Пусть производиться n независимых опытов. Событие A в i - ом опыте может произойти с вероятностью
Доказательство.
Применяя её, получим
Раздел 10. Предельные теоремы теории вероятностей. Центральная предельная теорема. Центральная предельная теорема теории вероятностей представляет собой совокупность предложений, устанавливающих условия возникновения нормального закона распределения. Пусть на
Рассмотрим случайные величины
и установим условия, при которых распределение случайной величины Будем говорить, что последовательность случайных величин Заметим, что В самом деле, пусть
Здесь Положим
Поскольку
где
Случайную величину
где
Если
Теперь, учитывая теорему единственности, вопрос о
Этот прием будет основным в доказательстве следующей теоремы, дающей достаточное условие для Теорема Ляпунова. Пусть
Тогда
Доказательство. Прежде всего отметим, что выражение Далее, в выражение (10.2.2) для
где
Учитывая независимость
Отсюда следует
Разлагая в ряд по степеням
Отсюда найдем
В силу условия
Теперь можно записать
Отсюда следует требуемое
К числу простейших форм центральной предельной теоремы относится также теорема Лапласа. Теорема Лапласа. Если
Доказательство. Пусть
где Очевидно, существуют
В силу независимости испытаний случайные величины Таким образом, для рассматриваемых здесь случайных величин Следовательно, имеет место соотношение (10.2.2). Случайную величину
где
при условии независимости случайных величин Таким образом, доказано, что если выполнены условия теоремы Лапласа, то
Отсюда, учитывая определение стандартного нормального закона 2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.106.78 (0.006 с.) |

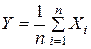 . Очевидно,
. Очевидно,  .
.

 , то при достаточно большом п
, то при достаточно большом п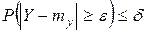

 – статистическая вероятность или частота появления события A в серии n – опытов.
– статистическая вероятность или частота появления события A в серии n – опытов. сходится к вероятности
сходится к вероятности  по вероятности, то есть
по вероятности, то есть или
или  .
. - число появлений события A в i – ом опыте.
- число появлений события A в i – ом опыте. 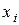



 ;
;  , то к ним можно применить теорему Чебышева, учитывая, что
, то к ним можно применить теорему Чебышева, учитывая, что  , тогда
, тогда  или
или 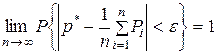
 ,
,  . Данные случайные величины удовлетворяют условиям обобщенной теоремы Чебышева.
. Данные случайные величины удовлетворяют условиям обобщенной теоремы Чебышева.
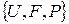 заданы независимые случайные величины
заданы независимые случайные величины  с числовыми характеристиками
с числовыми характеристиками

 с возрастанием п становится сколь угодно близким к нормальному N (0,1), т.е.
с возрастанием п становится сколь угодно близким к нормальному N (0,1), т.е. 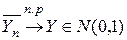 .
. удовлетворяет центральной предельной теореме, если
удовлетворяет центральной предельной теореме, если  .
. существует
существует  , что при
, что при  выполняется условие
выполняется условие
 - функция распределения
- функция распределения 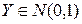 .
. . Тогда для
. Тогда для  :
:

 – распределение
– распределение  , а
, а 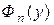 - распределение
- распределение 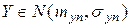 ,то вместо (10.1.3) можно записать:
,то вместо (10.1.3) можно записать:

 - независимые случайные величины с характеристиками
- независимые случайные величины с характеристиками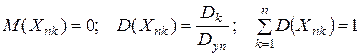
 - характеристическая функция
- характеристическая функция  , то характеристическая функция
, то характеристическая функция  случайной величины
случайной величины  имеет вид:
имеет вид: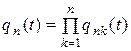
 можно свести к установлению сходимости
можно свести к установлению сходимости
 - независимые и одинаково распределенные случайные величины с числовыми характеристиками
- независимые и одинаково распределенные случайные величины с числовыми характеристиками

 , случайных величин
, случайных величин  , поэтому доказательство можно проводить, полагая в (10.2.2)
, поэтому доказательство можно проводить, полагая в (10.2.2)  , т.е. при условиях
, т.е. при условиях
 - независимые и одинаково распределенные. Поскольку
- независимые и одинаково распределенные. Поскольку  , одинаково распределены, то их характеристические функции совпадают:
, одинаково распределены, то их характеристические функции совпадают:
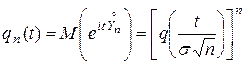

 правую часть уравнения (10.2.5) при достаточно больших п получим с учетом теоремы о дифференцируемости характеристических функций
правую часть уравнения (10.2.5) при достаточно больших п получим с учетом теоремы о дифференцируемости характеристических функций

 и формулы
и формулы  получим
получим


 - число появлений случайного события А в п независимых повторных испытаниях с исходами
- число появлений случайного события А в п независимых повторных испытаниях с исходами  , вероятности которых
, вероятности которых  , то
, то
 .
.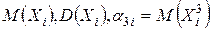





 , находим, что соотношение (10.3.1) справедливо.
, находим, что соотношение (10.3.1) справедливо.


