
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Независимые испытания. Формулы Бернулли.Содержание книги
Поиск на нашем сайте
В настоящем разделе мы изучим основные закономерности, относящиеся к одной из важнейших схем теории вероятностей — схеме последовательных независимых испытаний. В это понятие мы вкладываем следующий смысл. Под испытанием(опытом) мы станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства U элементарных событий. Математической моделью последовательности п испытаний является новое пространство Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных состояний состоит из 6 точек. Пространство Пусть под испытанием понимается проверка длительности безотказной работы полупроводникового прибора под определенным напряжением. Пространство элементарных событий состоит из множества точек полупрямой Предположим, что для s-го испытания пространство U разбито на k несовместимых случайных событий
Событие Bernylli Обозначим через В дальнейшем мы ограничимся случаем, когда вероятности событий Из определения независимых испытаний вытекает следующий результат: Теорема 1. Если данные п испытаний независимы, то любые т из них также независимы. Для простоты ограничимся случаем
из которого следует, что
По определению это означает, что первые п— 1 испытаний независимы. Простейшая задача, относящаяся к схеме независимых испытаний, состоит в определении вероятности
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В представляет собой сумму несовместных событий, тогда согласно теореме сложения вероятностей получаем
Вероятность каждого слагаемого в данной сумме по теореме умножения для независимых событий равна
Так как все возможные несовместимые между собой исходы п испытаний состоят в появлении события
Легко заметить, что вероятность Исследуем далее как ведет себя вероятность при различных значениях m. Найдем m, при котором вероятность
Из полученного соотношения следует: 1) Пусть 2) Пусть 3) Пусть Таким образом, Пример. Вероятность попадания при одном броске в кольцо равна 0,4. Баскетболист совершил 10 бросков. Каково наивероятнейшее значение числа попаданий в кольцо?
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.189 (0.009 с.) |

 элементарных событий, состоящее из точек
элементарных событий, состоящее из точек  , где
, где  - произвольная точка пространства U, отвечающая испытанию с номером i.
- произвольная точка пространства U, отвечающая испытанию с номером i. , соответствующее трем испытаниям, состоит из 216 точек(n=63).
, соответствующее трем испытаниям, состоит из 216 точек(n=63).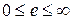 . Пространство
. Пространство  , т. е. предположим, что
, т. е. предположим, что
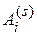 назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через
назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через  = Р (
= Р ( событие, состоящее из всех тех точек
событие, состоящее из всех тех точек  . Если в пространстве Un имеет место равенство
. Если в пространстве Un имеет место равенство  при любых
при любых 
 - то испытания называются независимыми.
- то испытания называются независимыми. ; в силу несовместимости и единственной возможности исходов
; в силу несовместимости и единственной возможности исходов  . Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае
. Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае  ; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают
; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают 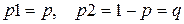 .
. , поскольку переход к общему случаю не встречает затруднений. Действительно, имеет место очевидное равенство
, поскольку переход к общему случаю не встречает затруднений. Действительно, имеет место очевидное равенство
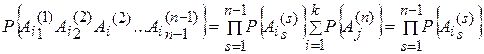
 того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие
того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие 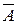 , обозначим это событие В. Тогда
, обозначим это событие В. Тогда

 . По теореме сложения вероятностей искомая вероятность
. По теореме сложения вероятностей искомая вероятность  равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно
равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно  ; следовательно, искомая вероятность равна
; следовательно, искомая вероятность равна
 0 раз, 1 раз, 2 раза,..., n раз, то ясно, что
0 раз, 1 раз, 2 раза,..., n раз, то ясно, что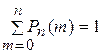
 в разложении бинома
в разложении бинома  по степеням x.
по степеням x.
 - в данном случае вероятность возрастет с ростом m.
- в данном случае вероятность возрастет с ростом m. - тогда предыдущая и последующая вероятности выравниваются.
- тогда предыдущая и последующая вероятности выравниваются.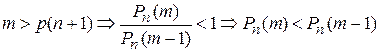 - в данном случае вероятность уменьшается с ростом m.
- в данном случае вероятность уменьшается с ростом m.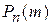 с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если
с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если  является целым числом, то максимальное значение вероятность
является целым числом, то максимальное значение вероятность  и
и  . Если же
. Если же  , равном максимальному целому числу, большему из
, равном максимальному целому числу, большему из  и
и  . Число
. Число  называют наивероятнейшим значением и обозначают через
называют наивероятнейшим значением и обозначают через  .
.



