
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость последовательностей случайных величин.Содержание книги
Поиск на нашем сайте
Пусть на вероятностном пространстве Определение 1. Последовательность
Обозначим сходимость Определение 2. Последовательность
Обозначим эту сходимость символом Определение 3. Говорят, последовательность
Обозначим эту сходимость символом Определение 4. Последовательность
Здесь Fn,F- функции распределения Xn и X, причем сходимость {Fn} к F подразумевается для всех x, за исключением, может быть, точек разрыва F. Сходимости {Xn} к X, введенные определениями 1-4, связаны между собою отношениями, показанными на рис. 9.1.1.
Рис. 9.1.1. Закон больших чисел. Рассмотрим ряд теорем, образующих группу теорем закона больших чисел. В качестве леммы необходимой для доказательства теорем докажем важное общее неравенство, известное под названием неравенства Чебышева. Неравенство Чебышева. Пусть имеется случайная величина X с математическим ожиданием тх и дисперсией Dx. Неравенство Чебышева утверждает, что, каково бы ни было положительное число
Доказательство. 1. Пусть величина X дискретная, с рядом распределения:
Изобразим возможные значения величины X и ее математическое ожидание тх в виде точек на числовой оси Ох (рис. 9.2.1). Зададимся некоторым значением
Для этого отложим от точки тх вправо и влево по отрезку длиной а; получим отрезок АВ. Вероятность (9.2.1) есть не что иное,
как вероятность того, что случайная точка X попадет не внутрь отрезка АВ, а вовне его:
Для того чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значении xi, которые лежат вне отрезка АВ. Это мы запишем следующим образом:
где запись С другой стороны, напишем выражение дисперсии величины X. По определению:
Так как все члены суммы (9.2.4) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения xi, а только на некоторые, в частности на те, которые лежат вне отрезка АВ:
Заменим под знаком суммы выражение
Но согласно формуле (9.2.3) сумма, стоящая в правой части (9.2.6). есть не что иное, как вероятность попадания случайной точки вовне отрезка АВ; следовательно,
откуда непосредственно вытекает доказываемое неравенство. 2. В случае, когда величина X непрерывна, доказательство проводится аналогичным образом с заменой вероятностей pi элементам вероятности, а конечных сумм — интегралами. Действительно,
где f(x) — плотность распределения величины X. Далее, имеем:
где знак Заменяя
откуда и вытекает неравенство Чебышева для непрерывных величия. Теорема Чебышева. Пусть
Доказательство. Выше было показано, что величина
имеет числовые характеристики
Применим к случайной величине Y неравенство Чебышева:
Как бы мало ни было число
где
откуда, переходя к противоположному событию, имеем:
что и требовалось доказать. Обобщенная теорема Чебышева. Теорема Чебышева легко может быть обобщена на более сложный случай. Обобщенная теорема Чебышева формулируется следующим образом. Если
то при возрастании п среднее арифметическое наблюденных значений величин
Доказательство. Рассмотрим величину
Ее математическое ожидание равно:
а дисперсия
Применим к величине Y неравенство Чебышева:
или
Заменим в правой части неравенства (9.2.7) каждую из величин
Как бы мало ни было Теорема Маркова. Закон больших чисел может быть распространен и на зависимые случайные величины. Обобщение закона больших чисел на случай зависимых случайных величин принадлежит А. А. Маркову. Теорема. Если имеются зависимые случайные величины
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.200.112 (0.008 с.) |

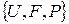 определены случайные величины
определены случайные величины 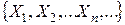 со значениями
со значениями 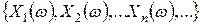 .
. сходится по вероятности (п.в) к величине X, если
сходится по вероятности (п.в) к величине X, если
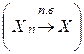 .
.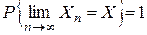
 .
.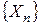 сходится к X в среднеквадратическом (с.к.), если
сходится к X в среднеквадратическом (с.к.), если
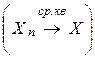 .
.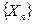 сходится к X по распределению (п.р) с обозначением
сходится к X по распределению (п.р) с обозначением 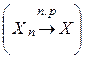 , если
, если

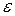 , вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на
, вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на  , ограничена сверху величиной —
, ограничена сверху величиной — 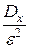 :
: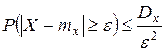
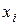
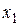

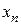
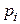
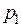

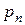
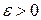 и вычислим вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на
и вычислим вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на 


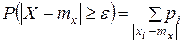
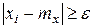 под знаком суммы означает, что суммирование распространяется на все те значения i, для которых точки
под знаком суммы означает, что суммирование распространяется на все те значения i, для которых точки 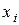 лежат вне отрезка АВ.
лежат вне отрезка АВ.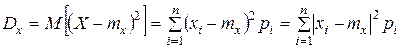
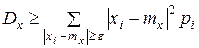
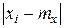 через
через 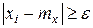 , то от такой замены сумма тоже может только уменьшиться; значит.
, то от такой замены сумма тоже может только уменьшиться; значит.

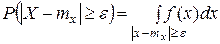
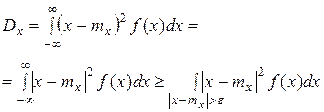
 под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка АВ.
под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка АВ. под знаком интеграла через
под знаком интеграла через 
 последовательность независимых случайных величин, имеющих одинаковые
последовательность независимых случайных величин, имеющих одинаковые 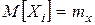 и
и 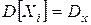 . Тогда при
. Тогда при  их среднее арифметическое сходится по вероятности к их математическому ожиданию, то есть
их среднее арифметическое сходится по вероятности к их математическому ожиданию, то есть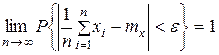
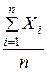
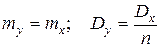

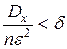
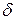 — сколь угодно малое число. Тогда
— сколь угодно малое число. Тогда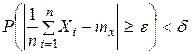
 , что эквивалентно
, что эквивалентно 
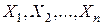 независимые случайные величины с математическими ожиданиями
независимые случайные величины с математическими ожиданиями  и дисперсиями
и дисперсиями  и если все дисперсии ограничены сверху одним и тем же числом L:
и если все дисперсии ограничены сверху одним и тем же числом L:
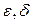 — сколь угодно малые положительные числа. Тогда при достаточно большом n
— сколь угодно малые положительные числа. Тогда при достаточно большом n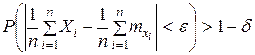
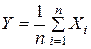
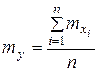


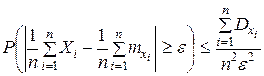
 большей величиной L. Тогда неравенство только усилится:
большей величиной L. Тогда неравенство только усилится: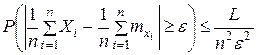
 , тогда
, тогда 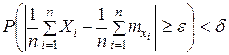 откуда, переходя к противоположному событию, получим доказываемое неравенство.
откуда, переходя к противоположному событию, получим доказываемое неравенство.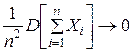 , то среднее арифметическое случайных величин
, то среднее арифметическое случайных величин 


