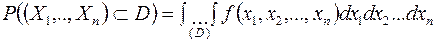Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики системы двух случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ранее в разделе 3.4. были введены числовые характеристики случайной величины важнейшими из которых являются моменты. Аналогичные числовые характеристики можно ввести и для системы двух случайных величин. Начальным моментом порядка k,s системы (X,Y) называется математическое ожидание произведения Xk на Ys:
Центральным моментом порядка k, s системы (X,Y) называется математическое ожидание произведения k -й и s -й степени соответствующих центрированных величин:
где Запишем формулы для непосредственного подсчета моментов. Для дискретных случайных величин
где Для непрерывных случайных величин:
где f(x, у) — плотность распределения системы. Помимо чисел k и s,характеризующих порядок момента по отношению к отдельным величинам, рассматривается еще суммарный порядок момента k+s, равный сумме показателей степеней при X и Y. Соответственно суммарному порядку моменты классифицируются на первые, вторые и т. д. На практике обычно применяются только первые и вторые моменты. Первые начальные моменты представляют собой уже известные нам математические ожидания величин X и Y, входящих в систему:
Совокупность математических ожиданий тх, ту представляет собой характеристику положения системы. Геометрически это координаты точки на плоскости, вокруг которой происходит рассеивание случайных точек (X,Y) Кроме первых начальных моментов, на практике широко применяются еще вторые центральные моменты системы. Два из них представляют собой уже известные нам дисперсии, величин X и Y.
характеризующие рассеивание случайной точки в направлении осей Ох и Оу, относительно вектора математических ожиданий. Особую роль как характеристика системы играет второй смешанный центральный момент:
т.е. математическое ожидание произведения центрированных случайных величин. Ввиду того, что этот момент играет важную роль в теории систем случайных величин, введем для него особое обозначение:
Характеристика Кху называется корреляционным моментом (иначе — «моментом связи») случайных величин X, Y. Для дискретных случайных величин корреляционный момент выражается формулой
а для непрерывных — формулой
Выясним смысл и назначение этой характеристики. Корреляционный момент есть характеристика системы случайных величин, описывающая рассеивание случайных величин X и Y, а так жевероятностную связь между ними. Для того чтобы убедиться в этом, докажем, что для независимых случайных величин корреляционный момент равен нулю. Доказательство проведем для непрерывных случайных величин. Пусть X, Y — независимые непрерывные случайные величины с плотностью распределения f(x,у). Для независимых случайных величин
где
Интеграл
представляет собой не что иное, как первый центральный момент величины X, и, следовательно, равен нулю; по той же причине равен нулю и второй сомножитель; следовательно, для независимых случайных величин Таким образом, из независимости случайных величин X и Y следует их некоррелированность, если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависимости между ними. Корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин (X,Y) весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины (X,Y). Поэтому для характеристики связи между величинами (X,Y) в чистом виде переходят от момента Кху к безразмерной характеристике
где Случайные величины, для которых корреляционный момент (а значит, и коэффициент корреляции) равен нулю, называются некоррелированными (иногда — «несвязанными»). Выясним, эквивалентно ли понятие некоррелированности случайных величин понятию независимости. Выше мы доказали, что две независимые случайные величины всегда являются некоррелированными. Остается выяснить: справедливо ли обратное положение, вытекает ли из некоррелированности величин их независимость? Оказывается — нет. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми. Равенство нулю коэффициента корреляции — необходимое, но не достаточное условие независимости случайных величин.
Из некоррелированности величин еще не следует их независимость. Условие независимости случайных величин — более жесткое, чем условие некоррелированности. Убедимся в этом на примере. Рассмотрим систему случайных величин (X, Y), распределенную с равномерной плотностью внутри круга С радиуса r с центром в начале координат (рис. 5.6.1). Плотность распределения величин (X, Y) выражается формулой
тогда
Нетрудно убедиться, что в данном примере величины являются зависимыми. Действительно, если величина X приняла, например, значение 0, то величина Y может с равной вероятностью принимать все значения от - r до + r, если же величина X приняла значение r, то величина Y может принять только одно единственное значение, в точности равное нулю; вообще, диапазон возможных значений Y зависит от того, какое значение приняла X. Таким образом, мы видим, что из некоррелированности случайных величин не всегда следует их независимость. Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины X и Y связаны линейной функциональной зависимостью: В случае 5.7. Система произвольного числа случайных величин (случайные вектора). Определение 1. Функцией распределения системы п случайных величин
Определение 2. Плотностью распределения системы п непрерывных случайных величин называется n -я смешанная частная производная функции
Зная закон распределения системы, можно определить законы распределения отдельных величин, входящих в систему. Функция распределения каждой из величин, входящих в систему, получится, если в функции распределения системы положить все остальные аргументы равными
Если выделить из системы величин
Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам:
Плотность распределения подсистемы
Определение 3. Условным законом распределения подсистемы Условная плотность распределения ее может быть вычислена по формуле:
Случайные величины Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему:
Вероятность попадания случайной точки
Эта формула по существу является основной формулой для вычисления вероятностей событий, не сводящихся к схеме случаев.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.133.251 (0.011 с.) |



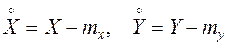
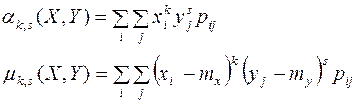
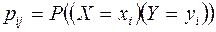 — вероятность того, что система (X,Y) примет значения
— вероятность того, что система (X,Y) примет значения  , а суммирование распространяется по всем возможным значениям случайных величин X,Y.
, а суммирование распространяется по всем возможным значениям случайных величин X,Y.

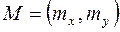 будем называть вектором математических ожиданий.
будем называть вектором математических ожиданий.


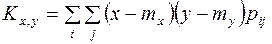
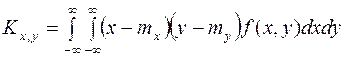
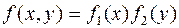
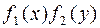 — плотности распределения соответственно величин X и Y.
— плотности распределения соответственно величин X и Y.

 .
.
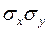 — среднеквадратические отклонения величин X,Y. Эта характеристика называется коэффициентом корреляции величин X и Y. Очевидно, коэффициент корреляции обращается в нуль одновременно с корреляционным моментом; следовательно, для независимых случайных величин, коэффициент корреляции равен нулю.
— среднеквадратические отклонения величин X,Y. Эта характеристика называется коэффициентом корреляции величин X и Y. Очевидно, коэффициент корреляции обращается в нуль одновременно с корреляционным моментом; следовательно, для независимых случайных величин, коэффициент корреляции равен нулю.
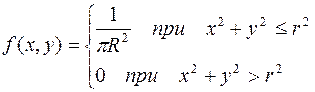

 , то
, то  , причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент а. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пределах:
, причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент а. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пределах:  говорят о положительной корреляции величин X и Y, в случае
говорят о положительной корреляции величин X и Y, в случае  — об отрицательной корреляции. Положительная корреляция между случайными величинами означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.
— об отрицательной корреляции. Положительная корреляция между случайными величинами означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать. называется вероятность совместного выполнения п неравенств вида
называется вероятность совместного выполнения п неравенств вида 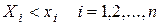 , то есть:
, то есть:
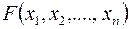 , взятая один раз по каждому аргументу:
, взятая один раз по каждому аргументу:
 :
:
 , то функция распределения этой подсистемы определяется по формуле
, то функция распределения этой подсистемы определяется по формуле


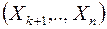 приняли значения
приняли значения  .
.
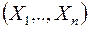 называются независимыми, если закон распределения каждой частной подсистемы, выделенной из системы
называются независимыми, если закон распределения каждой частной подсистемы, выделенной из системы