
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 2. Геометрическое определение вероятности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Краткая теоретическая часть. Сущность геометрического определения вероятности. Еще в самом начале развития теории вероятностей была замечена недостаточность «классического» определения вероятности, основанного на рассмотрении конечной группы равновероятных событий. Уже тогда частные примеры привели к некоторому видоизменению этого определения и построению понятия вероятности также для случаев, когда мыслимо бесконечное множество исходов. При этом по-прежнему основную роль играло понятие «равновероятности» некоторых событий. Общая задача, которая ставилась и привела к расширению понятия вероятности, может быть сформулирована следующим способом. Пусть, например, на плоскости имеется некоторая область G и в ней содержится другая область g с квадрируемой границей. В область G наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадет в область g. При этом выражению «точка бросается наудачу в область G» придается следующий смысл: брошенная точка может попасть в любую точку области G, вероятность попасть в какую-либо часть области G пропорциональна мере этой части (длине, площади и т. д.) и не зависит от ее расположения и формы. Таким образом, по определению, вероятность попадания в область g при бросании наудачу точки в область G равна Примеры. Рассмотрим несколько примеров. Пример 1. Задача о встрече. Два лица А и В условились Встретиться в определенном месте между 12 часами и часом. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течение указанного часа может произойти наудачу и моменты прихода независимы.
Решение. Обозначим моменты прихода лица А через х и лица В через у. Для того чтобы встреча произошла, необходимо и достаточно, чтобы
Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата:
Пример 2. Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросается игла длины 2l(l≤a). Найти вероятность того, что игла пересечет какую-нибудь прямую.
Решение. Обозначим через х расстояние от центра до ближайшей параллели и через
Искомая вероятность в силу сделанных предположений равна отношению площади заштрихованной на рис. 2.3. области к площади прямоугольника
Заметим, что задача Бюффона являлась исходным пунктом для решения некоторых проблем теории стрельбы, учитывающих размеры снаряда Тест 1. Применимо ли геометрическое определение вероятности, если число исходов опыта бесконечно? а) Да б) Нет
2. Пусть на плоскости имеется некоторая область G с квадрируемой границей и в ней содержится подобласть g. В область G наудачу бросается точка. Определить, какова вероятность того, что точка попадет в подобласть g. Выберите условия, выполнение которых необходимо для того, чтобы эту задачу можно было бы решить с использованием геометрического определения вероятности. а) Точка может попасть в любую точку области G с равной вероятностью б) Вероятность попадания брошенной точки в каждую точку области G определяется по некоторому закону и необязательно одинакова в) Вероятность попадания точки в подобласть g зависит от ее формы и расположения г) Вероятность попадания точки в подобласть g не зависит от ее формы и расположения д) Вероятность попадания точки в какую-либо часть области G пропорциональна мере этой части (длине, площади и т.д.) е) Вероятность попадания точки в какую-либо часть области G не пропорциональна мере этой части
3. Если выполняются все необходимые условия для применения геометрического определения вероятности, то вероятность попадания в подобласть g при бросании наудачу точки в область G равна: а) P = mes g / mes G б) P = mes G / mes g в) P = 1 / mes G г) P = 1 / mes g д) P = mes G - mes g е) P = mes g mes G
4. В чем заключается основное преимущество геометрического определения вероятности над классическим?
а) Наглядность б) Возможность применения в случае бесконечного числа исходов опыта в) Нет необходимости в том, чтобы исходы опыта были равновозможны г) Никаких преимуществ нет, эти определения полностью эквивалентны
5. Какую из следующих задач нельзя решить с использованием геометрического определения вероятности? а) В большой лекционной аудитории объема V летает комар. Один из студентов выпустил струю газа инсектицида из баллончика, в результате чего образовалось облако объема v. Какова вероятность того, что комар попадет в это облако, если нахождение его в любой точке аудитории равновероятно и вероятность попадания в любую подобласть аудитории пропорциональна размерам этой подобласти. б) В лужу площади S падает камушек. Определить вероятность того, что камушек упадет на монетку, лежащую на дне, если и камушек, и монетка рассматриваются как материальные точки, расположение монетки в луже известно заранее, а попадание камушка в любое место лужи равновозможно. в) В круг радиуса R помещен меньший круг радиуса r.Определить вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения. г) Все задачи можно решать с использованием геометрического определения вероятности. д) Ни к одной из перечисленных задач геометрическое определение неприменимо. Решение типовых задач Пример 2.1. На горизонтальной плоскости вдоль прямой АВ через интервал l расположены оси одинаковых вертикальных цилиндров с радиусом основания г. Под углом q к прямой бросается шар радиуса R. Определить вероятность столкновения шара с цилиндром, если пересечение линии движения центра шара с прямой АВ равновозможное в любой точке.
Решение. Введем в рассмотрение событие А, состоящее в том, что произойдет столкновение шара с цилиндром. Пусть х — расстояние от центра шара до ближайшей линии, проходящей через центр цилиндра параллельно направлению перемещения центра шара. Возможные значения x определяются условиями (рис.1):
Столкновение шара с цилиндром произойдет в том случае, если Искомая вероятность равна отношению длин отрезков, на которых находятся благоприятствующие и все возможные значения x. Поэтому
Пример 2.2. На одной дорожке магнитофонной ленты длиной 200 м записано сообщение на интервале 20 м, на второй — записано аналогичное сообщение. Определить вероятность того, что в интервале от 60 до 85 м не будет промежутка ленты, не содержащего записи, если начала обоих сообщений равновозможные в любой точке от 0 до 180 м. Решение. Введем в рассмотрение событие А, состоящее в том, что в интервале от 60 до 85 м не будет промежутка ленты, не содержащего записи. Пусть x и у — координаты начала записей, причем Найдем область значений x и у, благоприятствующих указанному событию. Для того чтобы получилась непрерывная запись, необходимо выполнение неравенства
Пример 2.3. В любые моменты промежутка времени Т равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше Решение.
Пусть x и у — моменты поступления сигналов в приемник. Областью возможных значений x, у является квадрат площадью T2 (рис. 3). Приемник будет забит, если Ее площадь Пример 2.4. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше
Решение. Введем в рассмотрение событие А, состоящее в том, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше
Вторая граница 2.4. Задачи для самостоятельной работы 2.1. В точке С, положение которой на телефонной линии АВ длины L равновозможно, произошел разрыв. Определить вероятность того, что точка С удалена от точки A на расстояние, не меньшее l. (Ответ: p =
2.2. На плоскости проведены параллельные линии, расстояния между которыми попеременно равны 1,5 и 8 см. Определить вероятность того, что наудачу брошенный на эту плоскость круг радиуса 2,5 см не будет пересечен ни одной линией. (Ответ: p =
2.3. В круге радиуса R проводятся хорды параллельно заданному направлению. Какова вероятность того, что длина наугад взятой хорды не более R, если равновозможны любые положения точек пересечения хорды с диаметром, перпендикулярным выбранному направлению? (Ответ: p = 0.134)
2.4. Перед вращающимся с постоянной скоростью диском находится отрезок длиной 2 h, расположенный в плоскости диска таким образом, что прямая, соединяющая середину отрезка с центром диска перпендикулярна отрезку. По касательной к окружности в произвольный момент времени слетает частица. Определить вероятность попадания этой частицы на отрезок, если расстояние между отрезком и центром диска равно l.
(Ответ: p =
2.5. Прямоугольная решетка состоит из цилиндрических прутьев радиуса r. Расстояния между осями прутьев равны соответственно a и b. Определить вероятность попадания шариком диаметра d в решетку при одном бросании без прицеливания, если траектория полета шарика перпендикулярна плоскости решетки. (Ответ: p =
2.6. Начерчены пять концентрических окружностей, радиусы которых равны соответственно kr (k =1, 2, 3, 4, 5). Круг радиуса r и два кольца с внешними радиусами 3 r и 5 r заштрихованы. В круге радиуса 5 r наудачу выбрана точка. Определить вероятность попадания этой точки: а) в круг радиуса 2 r; б) в заштрихованную область. (Ответ: а) p = 0,16; б) p = 0.6)
2.7. Лодка перевозит груз с одного берега пролива на другой, пересекая пролив за один час. Какова вероятность того, что идущее вдоль пролива судно будет замечено, если с лодки обнаруживают судно в случае, когда пересекают его курс не ранее, чем за 20 мин. до пересечения судком курса лодки, и не позднее, чем через 20 мин. после пересечения судном курса лодки? Любой момент и любое место пересечения судном курса лодки равновозможны. Курс судна перпендикулярен курсу лодки. (Ответ: p =
2.8. На отрезке длиной l наудачу выбраны две точки. Какова вероятность, что расстояние между ними меньше kl, где (Ответ: p = k (2- k))
2.9. На отрезке АВ длиной l наудачу поставлены две точки L и М. Найти вероятность того, что точка L будет ближе к точке М, чем к точке А. (Ответ: p = 0.75)
2.10. На отрезке длиной l наудачу ставятся две точки, в результате чего этот отрезок оказывается разделенным на три части. Определить вероятность того, что из трех получившихся частей отрезка можно построить треугольник. (Ответ: p =
2.11. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, а второго — два часа. (Ответ: p = 0,121)
2.12 Два лица имеют одинаковую вероятность прийти к указанному месту в любой момент промежутка времени Т. Определить вероятность того, что время ожидания одним другого будет не больше t. (Ответ: p =
2.13. Два судна в тумане: одно идет вдоль пролива шириной L, а другое курсирует без остановок поперек этого пролива перпендикулярно курсу первого. Скорости движения судов соответственно равны (Ответ: p =
2.14. Стержень длиной l =200 мм наудачу ломается на части. Определить вероятность того, что хотя бы одна часть стержня между точками излома будет не более 10 мм, если точек излома
а) две; б) три, причем излом стержня равновозможен в любом месте. (Ответ: а) p =
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.175 (0.011 с.) |

 .
. .
.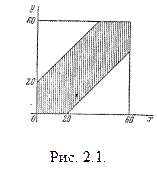 Будем изображать хOу как декартовы координаты на плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60; благоприятствующие встрече — расположатся в заштрихованной области (рис. 2.1).
Будем изображать хOу как декартовы координаты на плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60; благоприятствующие встрече — расположатся в заштрихованной области (рис. 2.1).
 —угол, составленный иглой с этой параллелью. Величины х и
—угол, составленный иглой с этой параллелью. Величины х и 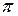 . Из рис. 2.2. видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы
. Из рис. 2.2. видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы  .
.



 .
.
 . Так как
. Так как  , то областью возможных значений x и у является, треугольник с катетами по 180 м. Площадь этого треугольника
, то областью возможных значений x и у является, треугольник с катетами по 180 м. Площадь этого треугольника  .
. . Чтобы интервал записи был не менее 25 м, должно быть
. Чтобы интервал записи был не менее 25 м, должно быть  . Кроме того, для получения непрерывной записи на интервале от 60 до 85м должно быть
. Кроме того, для получения непрерывной записи на интервале от 60 до 85м должно быть 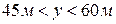 ,
,  .
. Проведя границы указанных областей, получим, что благоприятствующие значения x и y заключены в треугольнике, площадь которого
Проведя границы указанных областей, получим, что благоприятствующие значения x и y заключены в треугольнике, площадь которого  (рис. 2). Искомая вероятность равна отношению площади SБ, попадание в которую благоприятствует данному событию, к площади области S возможных значений x и у, т. е.
(рис. 2). Искомая вероятность равна отношению площади SБ, попадание в которую благоприятствует данному событию, к площади области S возможных значений x и у, т. е.  .
. . Определить вероятность того, что приемник будет забит.
. Определить вероятность того, что приемник будет забит. Введем в рассмотрение событие А, состоящее в том, что приемник будет забит.
Введем в рассмотрение событие А, состоящее в том, что приемник будет забит. . Данная область лежит между прямыми
. Данная область лежит между прямыми  и
и  .
. , поэтому
, поэтому 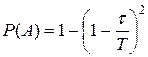 .
. ?
?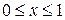 ,
,  , что на плоскости соответствует квадрату с площадью S =1. Благоприятствующие значения удовлетворяют условиям:
, что на плоскости соответствует квадрату с площадью S =1. Благоприятствующие значения удовлетворяют условиям:  и
и  .
. Граница
Граница  делит квадрат пополам, причем область
делит квадрат пополам, причем область 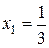 и
и  . Величина благоприятствующей площади
. Величина благоприятствующей площади  . Искомая вероятность
. Искомая вероятность  .
. )
) = 0.316)
= 0.316) )
) )
) )
) ?
? )
) )
) и
и  . Второе судно подает звуковые сигналы, которые слышны на расстоянии d < L. Определить вероятность того, что на первом судне услышат сигналы, если пересечение курсов судов равновозможно в любом месте пролива.
. Второе судно подает звуковые сигналы, которые слышны на расстоянии d < L. Определить вероятность того, что на первом судне услышат сигналы, если пересечение курсов судов равновозможно в любом месте пролива. )
) ; б) p =
; б) p =  ).
).


