
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение площади землепользования по координатам.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
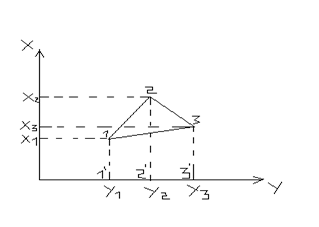
P=P1’12’+P2’233’ – P1’133’ Каждая полоса трапеция P=(a+b)h / 2 2P=(X2+X1)(Y2–Y1)+(X3+X2)(Y3–Y2)–(X3+X1)(Y3-Y1) Разложим это выражение по величинам X1 X2 X3 2P=x1(y2-y1-y3+y1)+ x2(y2-y1+y3-y2)+ x3(y3-y2-y3+y1) 2P= x1(y2-y3)+ x2(y3-y1)+ x3(y1-y2) 2P=∑xi(yi+1 – yi –1) 2P=∑yi(xi –1 – xi+1)
Формулы (75), (76) можно несколько преобразовать. Если (75) записать так
то получим
Поскольку
то (78) можно записать так
Если же положить, что
то
или
Формулу (83) легко переписать так
Она удобна для вычисления площадей по приращениям координат. §9. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ.
Для определения средней квадратической ошибки площади воспользуемся формулой (75). Дифференциалы p по x
Полагая, средние квадратические ошибки положения пункта по осям x и y равными
или с учетом (85), (86)
Приняв, что
где И обозначив
получим
Величина D Формула (91) весьма проста для вычислений, но ее еще упрощают для оценки точности площадей различных фигур. Пусть по формуле (91) оценивается площадь прямоугольника со сторонами S1 и S2. Тогда можно записать, что
Полагая S2=KS1 (92) перепишем
или
но
Тогда с учетом (95)
или
В случае, если на границах землепользования определены опорные межевые знаки, среднюю квадратическую ошибку общей площади можно определить по частям. Сначала вычисляется средняя квадратическая ошибка площадей участков, ограниченные звеньями границ и их замыкающими по формуле (91).
Рис. 3
-
-
Затем вычисляют среднюю квадратическую ошибку площади каркасного полигона, вершинами которого являются опорные межевые знаки
где Общая средняя квадратическая ошибка площади землепользования будет равна
где N – число звеньев.
§10. ГРАФИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ.
В данном способе участок (рис.4) разбивается на простейшие фигуры
Рис. 4 обычно треугольные. В каждом треугольнике измеряется по две высоты и по два основания. И по ним дважды определяется площадь треугольника
Если расхождения между этими значениями площади допустимо, то вычисляют среднюю площадь
Площадь участка тогда равняется сумме площадей отдельных треугольников. Для оценки точности настоящего способа запишем среднюю квадратическую ошибку площади треугольников
Полагая, что на плане
При a=h
Если разбить участок на прямоугольники, то тогда для каждого из них площадь определится так P = a – h, (104) где a и h – длина и ширина прямоугольника. Из (101) следует, что
При
Аналогично для проекций
где a, b, h – основания и высота проекций,
При равенстве средних квадратических ошибок и a = b = h найдем
Из сравнения формул (103), (106), (109) следует, что самой точной фигурой при определении площадей является треугольник. Если принять
то исходя из C можно записать
или
что соответствует
Поскольку площадь участка состоит из суммы площадей независимых треугольников, то на основании (113) можно записать среднюю квадратическую ошибку площади всего участка
Тогда
При m = 0.1 мм
Для масштаба плана 1:М формула (116) примет вид
Предельное значение ошибки площади будет
а предельная разность определений площади
Точность однократного определения площади палеткой равно
§11. ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ АНАЛИТИЧЕСКИМ СПОСОБОМ.
Аналитический способ определения площадей заключается в вычислении площади по результатам измерения линий и углов на местности. Он применим лишь к простым геометрическим фигурам: треугольнику и четырехугольнику. Могут быть выведены формулы для пяти - шестиугольников и других фигур. Но они являются громоздкими. Поэтому вместо них площади в полигонах вычисляют по координатам. Площадь треугольника (рис. 5) при измерении двух сторон и углу между ними определяется по формуле
Рис.5 Оценим точность площади. Продифференцировав (120) по измеренным величинам получим
Перейдя к средним квадратическим ошибкам найдем
Принимая треугольник близкий к равностороннему запишем
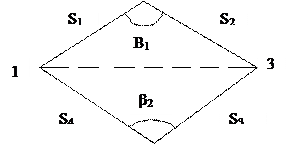
Рассмотрим теперь четырехугольник со всеми измеренными сторонами S1, S2, S3, S4 (рис. 6) и двумя противолежащими углами
Рис. 6 Тогда его площадь будет
Рис. 7
То его площадь определится как разность площадей двух треугольников 1А4 и 2А3, то есть P = (S1 + x) (S3 + y) sin γ – x * y sin γ (125) Поскольку
то с учетом этих выражений формула (125) примет вид
Оценим точность определения площадей способом (124) и способом (128) на основании (124) с учетом (123) для равностороннего четырехугольника можно записать
Полагая четырехугольник квадратом, то есть при β1 = β2 = 90˚, S1 = h и h * a = p (130) из (124) получим
или
Для оценки точности определения площади вторым способом продифференцируем (128) по результатам измерений и перейдем к средним квадратическим ошибкам
Если четырехугольник близок к квадрату, то
или
Полагая Запишем
Из сравнения формул (123) и (135) заключаем, что первый способ определения площади квадрата более точен.
§12. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ МЕХАНИЧЕСКИМ СПОСОБОМ.
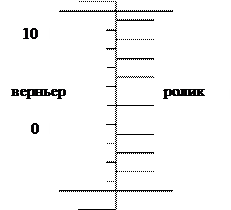
В механическом способе площадь определяется планиметром. В курсе геодезии излагается устройство планиметра, определение его цены деления, порядок определения площадей им и их увязка. В курсе прикладной геодезии рассматриваются поверки планиметра и вопроса точности определения площадей им. Планиметр должны удовлетворять основному геометрическому условию. Направление рифельных штрихов на ободке счетного ролика должно быть параллельно оси обходного рычага. Перед проверкой этого условия проверяются соблюдение следующих требований. 1. Счетный ролик должен свободно вращаться на оси, не задевать за верньер и не шататься в подшипниках. Для проверки этого требования приводят ролик в движение. Его вращение должно длиться 3 – 4 секунды. При этом зазор между роликом и верньером должны равняться толщине тонкой бумаги. Если что не выполняется, то отпустив стопорные винты Е и F регулировку выполняют винтами А и В. После регулировки винты F и Е закрываются. 2. Поверхность верньера должна быть продолжена поверхности рамки. Регулировка осуществляется закрепительными винтами верньера. Этими винтами он крепится с рамки счетного механизма. 3. Деление на рамке и верньере должны быть правильными. Для проверки, какой либо штрих рамки совмещают с начальным штрихом верньера. При этом конечный штрих верньера должен совместиться со штрихом рамки (рис. 9).
Рис. 9 Другими словами 10 делением верньера должно соответствовать 9 делением ролика. 4. Рифельные штрихи (рубчики) на ободке счетного ролика должны быть написаны правильно. Для проверки этого условиях используется контрольная линеечка, с помощью которой планиметром обводится круг. Обвод этого круга делают при остром (не менее 30°), прямом и тупом (не более 150°) углах планиметра. При каждом положении делается не менее 10 обводов. Колебания разности отсчетов при каждом положении не должно превосходить 3 деления планиметра. При недопустимых колебаниях планиметр исправляется в мастерской. 5. Основное геометрическое условие: направление рифельных штрихов на ободке счетного ролика должно быть параллельно оси обводного рычага. Для проверки этого условия обводят фигуру (лучше круг с использованием контрольной линеечки) при двух положениях полюса планиметра. При каждом положении полюса делается четыре обвода. По ним находится средняя разность отсчетов. Расхождение между разностями при полюсе право и полюсе лево не должно превосходить 3 деления. Если расхождение большее, то исправление осуществляется вращением винта N при открепленном стопорном винте. При вращении винта N счетный механизм поворачивается вокруг выступа G, им достигается параллельность направления рифельных штрихов к обводному рычагу. Площадь в механическом способе определяется по формуле: P = p * u, (135) где p – цена деления планиметра, u – число делений планиметра, полученного в результате обвода фигуры. Средняя квадратическая ошибка определения площади одним обводом планиметра вычисляется по следующей эмпирической формуле:
§13. ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ ПО СПОСОБУ САВИЧА.
Этот способ принимается для больших участков, состоящих из квадратов координатной сети. Общая площадь такого участка равна сумме площадей полных и неполных квадратов (рис.10). 6) где Р0 – площадь, составленная из полных квадратов. Площадь неполного квадрата определяется следующим образом.
Рис. 10
Внешнюю часть неполного квадрата обозначим через b, а внутреннюю через а. Планиметром обводятся в отдельности часть а и часть Р. В результате получается площади Ра и Рb. Примем, что а – площадь в делении планиметра части а, а b – площадь в делениях части b. Обводится также и весь квадрат. Его площадь известна и составляет Р. В делениях планиметра она, равна a+b. Между площадями и им соответствующих делений планиметра существуют следующие отношения:
Тогда
Исходя из формул () следует, что По определениям для всех неполных квадратов площадям P1i находится общая площадь участка:
§14. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ РАЙОНА И ОБЛАСТИ. К настоящему времени во всех геодезических работах применяется проекция Гаусса-Крюгера на базе шести, трех и одноградусных зон. Если применять одноградусные зоны, то поправки в линейные измерения при выполнении геодезических работ в кадастре можно не вводить и непосредственно вычисленные координаты, например, теодолитного хода, проложенного по границе земельного участка можно считать координатами проекции Гаусса-Крюгера. В случае использования шести и трехградусных зон поправки в линейные измерения следует вводить. Административные районы (рис. 11), расположенный в проекции Гаусса-Крюгера, состоит из отдельных проекций: полных и неполных.
Его площадь состоит из суммы площадей всех трапеций. Если эти площади вычислять в проекции Гаусса-Крюгера, то для получения площадей на эллипсоиде в них необходимо внести поправки по формулам, выведенным в сфероидической геодезии и приведенным ниже. В данном случае площадь района будем вычислять в проекции Гаусса-Крюгера. Площадь каждой полной трапеции определяется по координатам ее вершин в соответствии с одной из выведенных ранее формул, например,
Площади неполных трапеций определяются таким же образом, но здесь дополнительно находятся координаты точек пресечения меридианов и параллелей, изобразившихся в проекции Гаусса-Крюгера с линиями 1 – 2, 2 – 3, проложенными на границе районов. Покажем это на примере одной неполной трапеции (рис. 12).
На рисунке 12 трапеции ABCD разделена границей участка, которая закреплена точками 1, 2, 3, … Будем считать, что координаты точек 1, 2, 3 определены в системе Гаусса-Крюгера относительно опорных точек I, II, … Граница района пересекает трапецию ABCD в двух точках: E и F. Для вычисления неполной трапеции AE2FC необходимо иметь координаты точек E и F. Стороны проекции ABCD примем прямоугольными. Это допущение справедливо лишь для трапеций карт масштаба 1:1000 и крупнее. В дальнейшем будет оценена ошибка такого допущения. Принимая стороны трапеций прямоугольными составим два уравнения прямой по линии АВ и линии 1 –2.
Эти уравнения можно переписать так
Из решения находятся координаты x, y точки Е. Аналогично находятся координаты точки F. По полученным координатам находится площадь участка AE2FC. Для контроля находят площадь участка EBDF2. Сумма этих площадей должна равняться общей площади проекции ABCD. Допустимое расхождение между этими величинами оценивается следующим образом. Пусть в качестве элементарных приняты трапеции масштаба 1:1000. Их значения на эллипсоиде можно получить по формулам сфероидической геодезии. Эти же площади можно получить по координатам вершин трапеций с исправлением за переход на эллипсоид. Из сравнения этих площадей следует, что площадь вычисленная по координатам Гаусса-Крюгера меньше площади, полученной на эллипсоиде. Это вызвано двумя причинами: а) криволинейные параллели и меридианы в проекции Гаусса-Крюгера заменены их стягивающими хордами; б) площадь S1 между южной параллелью S и хордой больше чем площадь S между северной параллелью и хордой (рис. 13).
Рис. 13 Приведенное расхождение между площадями зависит от месторасположения трапеции. Так для широт от 50° и до 56° среднее расхождение составляет величину 2 м2. То есть площадь вычисленная по координатам Гаусса-Крюгера и исправленная за переход на эллипсоид меньше ее значения на эллипсоиде на 2м2. Если координаты углов трапеций получить с точностью 0.001 м, то средняя квадратическая ошибка их округления составит
Средняя квадратическая ошибка площади фигуры, близкой к квадрату вычисляется по формуле: Как видим округление до координат 0.001 м приводит к средней квадратической ошибке равной 1.8 м2. Определим теперь предельный интервал, в котором может находится ошибка площади трапеции. Для этого найдем предельную ошибку площади из-за округления.
Площадь, вычисленная по координатам в проекции Гаусса-Крюгера и исправления за переход на эллипсоид меньше площади на эллипсоиде на постоянную величину
А левый предел будет
Для трапеций масштаба 1:1000 будет a = 5.4 м2 – 2 = +3.4. м2 b = - 5.4 м2 – 2 = 7.4 м2 Таким образом, расхождение площади трапеции вычисляемой по геодезическим координатам на эллипсоиде, с суммой площадей частей трапеции, вычисленных по координатам, не должна выпадать за пределы от + b до – а. В данном примере от + 7.4 м2 до – 3.4 м2.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.15.124 (0.008 с.) |

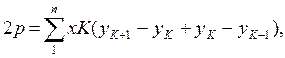 (77)
(77)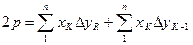 (78)
(78)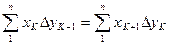 (79)
(79)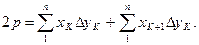 (80)
(80)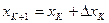 , (81)
, (81) (82)
(82)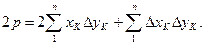 (83)
(83) (84)
(84) и y
и y  (85)
(85)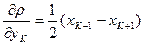 (86)
(86)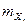
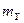 запишем, квадрат средней квадратической ошибки площади
запишем, квадрат средней квадратической ошибки площади 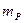 в виде
в виде (87)
(87) (88)
(88) (89)
(89) - средняя квадратическая ошибка положения граничной точки земельного участка.
- средняя квадратическая ошибка положения граничной точки земельного участка.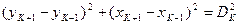 (90)
(90) (91)
(91) (92)
(92)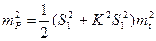 (93)
(93)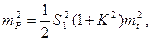 (94)
(94)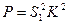 (95)
(95)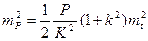 (96)
(96) (97)
(97)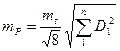 (98)
(98)

 опорные межевые знаки
опорные межевые знаки


 межевые знаки на границе земельного участка.
межевые знаки на границе земельного участка.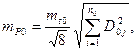 (99)
(99) - средняя квадратическая ошибка положения опорного межевого знака;
- средняя квадратическая ошибка положения опорного межевого знака;  - диагональ соединяющая j-1 и j+1 опорные межевые знаки;
- диагональ соединяющая j-1 и j+1 опорные межевые знаки; 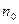 - число вершин каркасного полигона.
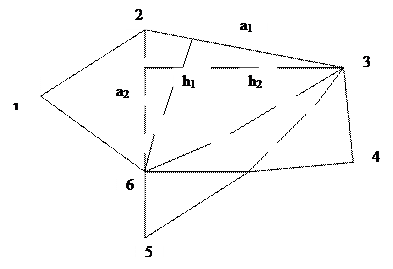
- число вершин каркасного полигона. (100)
(100)
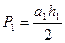
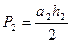
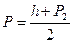
 (101)
(101) получим
получим (102)
(102)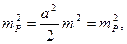 (103)
(103) (105)
(105)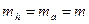 и a = h найдем
и a = h найдем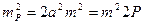 (106)
(106)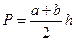 , (107)
, (107) (108)
(108) (109)
(109) (110)
(110)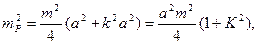 (111)
(111) (112)
(112)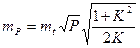 (113)
(113)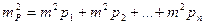 (114)
(114)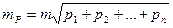 (115)
(115) (116)
(116) (117)
(117)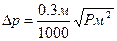 (118)
(118) (119)
(119)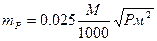
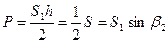 (120)
(120)
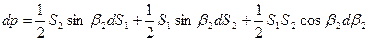 (121)
(121)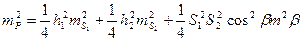 (122)
(122) (123)
(123)
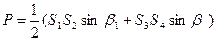 (124)
(124) Если в четырехугольнике измерены лишь три стороны и два смежных угла (рис. 7)
Если в четырехугольнике измерены лишь три стороны и два смежных угла (рис. 7) (126)
(126)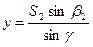 (127)
(127) (128)
(128) (129)
(129)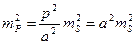 (131)
(131)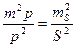 (132)
(132)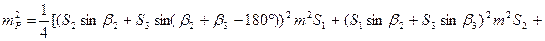

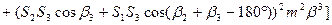 (133)
(133)
 (134)
(134)
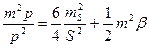 (135)
(135)
 (136)
(136)
 (136)
(136)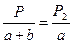
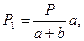 (137)
(137)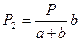
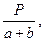 есть цена деления планиметра, она определяется в каждом неполном квадрате. Расхождение между ними допускается
есть цена деления планиметра, она определяется в каждом неполном квадрате. Расхождение между ними допускается  от величины цены деления.
от величины цены деления. (138)
(138) Рис. 11
Рис. 11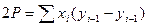 .
.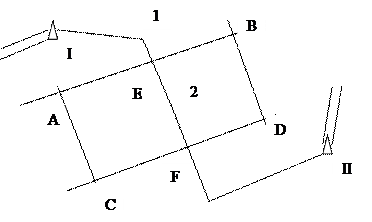 Рис. 12
Рис. 12


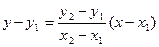

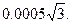 Принимая ошибки по осям координат равными запишем среднюю квадратическую ошибку точки равной:
Принимая ошибки по осям координат равными запишем среднюю квадратическую ошибку точки равной: .
. где Р – площадь фигуры.
где Р – площадь фигуры.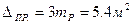
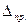 Тогда правая граница ошибки составит величину
Тогда правая граница ошибки составит величину




