Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии точности положения определяемого пункта.Содержание книги
Поиск на нашем сайте
Согласно инструкции по межеванию земель различают следующие критерии: 1. ср. кв. ошибка взаимного положения пунктов ОМС. 2. ср. кв. ошибка положения определяемого пункта относительно исходного. В данном случае под определяемым понимается межевой знак,а исходным считается, например пункт ОМС.
Выведем критерий точности положения определяемых пунктов. Пусть даны два пункта 1 и 2. Корреляционная матрица корд. этих пунктов равна: Qх1х1 Qх2у1 Qх1х2 Qх1у2 К = σ2 Qу1х1 Qу1у1 Qу1х1 Qу1у2 Qх2х2 Qх2у1 Qх2х2 Qх2у2 Qу2х1 Qу2у1 Qу2х2 Qу2у2
Корреляционная матрица определяет положение пунктов 1 и 2, относительно исходных, поэтому критериями положения пунктов будут стандарты этих пунктов: σ21 σ2 (Qх1х1 + Qу1у1), σ21 σ2 (Qх2х2 + Qу2у2) Взаимное положение пунктов можно представить след. векторами: ∆х = х2 – х1, ∆у = у2 – у2; или
х =
∆ - вектор взаимного положения пунктов. Найдем кореляц. матрицу этого вектора К∆ = АКАт, найдем произведение АК:
АК = ·К = σ2 *
∆КАт = ∆К =
= σ2 *
В этих выражениях Qх1х2 = Qх2х1 = 0, Qу2у1 = Qу1у2 = 0 Выведенная матрица взаимного положения пунктов. Но она не удобная, для простоты взаимное положение выражают одним числом, для этого можно найти сумму диагональных элементов этой матрицы, для простоты можно принять недиагональные = 0 и обратить обратно весовые коэффициенты выражающие корреляцию между величинами. Тогда в упрощенном выражении:
К∆ = АКАт = σ2 *
Qх1х1 – это обратный вес положения точки 1 по оси х; Qх2х2 – это обратный вес положения точки 2 по оси х; Qу1у1 – это обр. вес положения точки 1 по оси у; Qу2у2 – обр. вес положение точки 2 по оси у. Однако, в инструкции взаимное положение точек дано одним числом. Здесь сумма диагональных элементов выражается одним числом и тогда можно записать, что σ∆ = σ2(Qх1х1+Qч2ч2+Qy1y1+Qy2y2), где σ∆ - стандарт взаимного положения
, где σ1 σ2 – стандарты положения пунктов.
σ∆ = σ21 + σ22 Если же σ1 = σ2 = σt, тогда σ2∆ = 2σ2t Квадрат стандарта взаимного положения = двум квадратам стандарта положения точки. Исходя из этой матрицы можно вывести несколько критерий взаимного положения этих пунктов:
1. σ∆ = σt*√2 2. В качестве взаимного расположения точек может быть определено и расстояние
S =, тогда критерием точности взаимного расположения может рассматриваться стандарт расстояния S. σ2s = cos2α σ2x1 + cos2α σ2x2 + sin2α σ2y1 + sin2α σ2y2 Приближенно будем считать, что σ2t = σ2х + σ2у, σх = σу = σt/√2, тогда запишем σ2s = (σt/√2)2+ (σt/√2)2 = σ2t Тогда вторым критерием взаимного положения будет: σ∆ = σs = σt. В практических случаях, в том числе и в инструкциях критермй должен быть указан.
Из теории математической обработки геодезических измерений известно, что точность положения определяемых пунктов геодезической сети определяется корреляционной матрицей – K. K = σ Где N Известно, что N = Aт *PA, (32) Где A – матрица уравнений поправок, P – матрица весов измерений, обычно диагональная. Строки матрицы A состоят из коэффициентов уравнений поправок выполненных измерений. Если выполняются лишь линейно-угловые измерения, то составляются уравнения поправок направлений
и сторон υs = - cos На этапе проектирования свободные члены значения не имеют, необходимо знать лишь коэффициенты. a = b = На этапе проектирования необходимо также задаваться и весовой матрицей ρ или весами проектируемых измерений. При этом вес измеренного направления ρн можно принять равным единице, а веса измерения сторон ρs при равноточном измерении установить из соотношения
где σs – стандарта измерения сторон. Тогда ρs = В результате проектного расчета необходимо определить σ и σs. Эти значения будут зависить от величины ρs, которая будет принятой при составлении весовой матрицы ρ. Полученную в результате обращения матрицу N Q = Где t – удельное число определенных пунктов. Коэффициент Q Точность положения определяемого пункта i определяется дисперсией общего положения σ На этапе проектирования из значений Q
и
После того, как найден стандарт измерения направлений из соотношения (37) вычисляется стандарт измерения сторон.
§4. ВЫЧИСЛЕНИЕ МАТРИЦЫ ВЕСОВЫХ КОЭФФИЦИЕНТОВ.
Вычисление матрицы весовых коэффициентов (38) можно осуществлять различными способами. Но наиболее распространенными являются способ Гаусса и способ модифицированных Жордановых исключений. Рассмотрим вначале способ Гаусса. Введем следующие обозначения матрицы N. N = Поскольку QN = E, (44) где E – единичная матрица то, очевидно, что для поиска первой строки коэффициентов матрицы Q необходимо решить систему уравнений:
Для поиска второй строки коэффициентов матрицы Q решается точно такая же система уравнений, но с вектором свободных членов (0 1 0 … 0) и т.д., последняя строка коэффициентов находится по вектору свободных членов (0 0 0 … 1). Решение системы (45) осуществляется по схеме Гаусса, улучшаемой в теории математической обработки геодезических измерений. В способе модифицированных жордановых измерений практически реализуется также схема Гаусса. Но благодаря компактности и прочности вычислений этот способ выделяется как вполне самостоятельный. Благодаря простоте вычислений его называют еще симплексными. Слово симплекс происходит от латинского simpe – просто. Если квадратную неособенную с положительным определителем матрицу обозначить следующим образом:
то цикл или шаг модифицированных жордановых исключений записываются так. Вначале выбирается один из элементов матрицы (46). Обычно при обращении матрицы выбирать диагональный элемент. И вначале берется первый диагональный элемент. Такой элемент называется разрешающим. Над ним выполняется шаг модифицированных жордановых исключений по следующим правилам. Разрешающий элемент заменяется обратной величиной. Остальные элементы разрешающей строки делятся на разрешающий элемент. Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знаки. Прочие элементы вычисляются по формуле: bij = Qij - Второй шаг жордановых исключений выполняется со вторым диагональным элементом уже преобразованный на первом шаге матрицы. Обращение будет завершено, когда будут перебраны все диагональные элементы в качестве разрешающих. Контролем обращения является равенство (44).
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.134.53 (0.007 с.) |



 А = ∆ =
А = ∆ =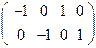

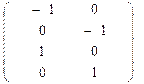


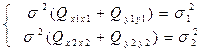

 * N
* N  , (31)
, (31) δн = - δz + aδx
δн = - δz + aδx  - bδy
- bδy  + bδy
+ bδy 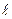 н (33)
н (33) δx
δx 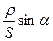
 (35) и соответственно значения
(35) и соответственно значения  (36)
(36)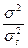 (37)
(37) (38)
(38)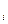 называют весомыми. При этом различают диагональные Q
называют весомыми. При этом различают диагональные Q  и недиагональные весовые коэффициенты.
и недиагональные весовые коэффициенты. = σ² (Q
= σ² (Q 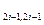 + Q
+ Q 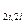 ) (39)
) (39)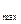 . Затем руководствуясь инструкцией по межеванию земель или более высокими требованиями по точности положения пунктов опорной межевой сети назначается стандарт положения пунктов геодезической опоры σомс. Тогда на основании (39) можно записать
. Затем руководствуясь инструкцией по межеванию земель или более высокими требованиями по точности положения пунктов опорной межевой сети назначается стандарт положения пунктов геодезической опоры σомс. Тогда на основании (39) можно записать =
=  Q
Q  (41)
(41) (42)
(42) (43)
(43) (45)
(45)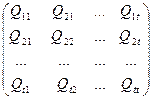 (46)
(46)